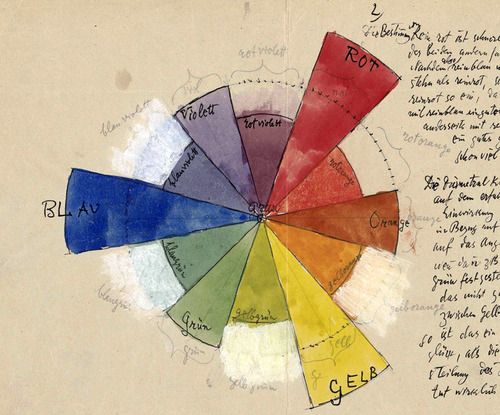
Farben

Wir hatten bislang noch wenig Gelegenheit, um über die Vektortypen von GLSL zu sprechen. Bevor es mit anderen Inhalten weitergeht, ist es wichtig, mehr über diese Variablentypen zu erfahren. Das Thema „Farben“ bietet sich dafür an.

Falls Du mit den Konzepten der objektorientierten Programmierung vertraut bist, ist Dir vielleicht schon aufgefallen, dass wir die verschiedenen Elemente innerhalb eines Vektors wie eine gewöhnliche struct in C ansprechen.

vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

Die Festlegung von Farben über die Komponenten x, y und z wirkt auf den ersten Blick etwas merkwürdig, nicht wahr? Aus diesem Grund gibt es weitere Möglichkeiten, um auf diese Elemente zuzugreifen. Die Inhalte von .x, .y und .z können auch als .r, .g und .b, sowie als .s, .t und .p angesprochen werden (.s, .t und .p werden typischerweise für die Raumkoordinaten von Texturen genutzt, wie wir in späteren Kapiteln noch sehen werden). Darüber hinaus lassen sich die Elemente eines Vektors auch über ihre Index-Position als [0], [1] und [2] ansprechen.

Die folgenden Programmzeilen zeigen die unterschiedlichen Ansätze, um jeweils auf die gleichen Vektorinhalte zuzugreifen:

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

Tatsächlich handelt es sich bei den unterschiedlichen Namen nur um verschiedene Bezeichner für jeweils ein und dieselbe Sache. Die Namen sollen Dir helfen, verständlichen Code zu schreiben, je nachdem, wofür ein Vektor gerade zum Einsatz kommt (Farben, Koordinaten, Raumpunkte etc.)

Ein weiteres praktisches Merkmal der Vektortypen in GLSL ist die Möglichkeit, ihre Eigenschaften in beliebiger Weise zu kombinieren. Das macht es besonders einfach, Werte zu tauschen und in andere Datentypen zu konvertieren. Diese Fähigkeit wird im Englischen als swizzle bezeichnet, was so viel wie „umrühren“ oder „mischen“ bedeutet.

vec3 yellow, magenta, green;

// Zusammenruehren von Gelb
yellow.rg = vec2(1.0);  // Zuweisung von 1. an den Rot- und den Gruen-Kanal von yellow
yellow[2] = 0.0;        // Zuweisung von 0. an den Blau-Kanal von yellow

// Zusammenruehren von Magenta
magenta = yellow.rbg;   // Zuweisung von yellow an magenta bei gleichzeitigem Tausch der Kanaele fuer Blau und Gruen

// Zusammenruehren von Gruen
green.rgb = yellow.bgb; // Zuweisung des Blau-Kanals von yellow an den Rot- und Blau-Kanal von green

Mischen von Farben

Jetzt, wo Du weißt, wie man Farben definiert, wird es Zeit, dies mit unserem bisher gesammelten Wissen zu verknüpfen. In GLSL gibt es eine äußerst praktische Funktion mit dem Namen mix(), über die man zwei Werte in Form von Prozentangaben mischen kann. Vielleicht kannst Du Dir bereits denken, wie diese Prozentangaben auszusehen haben? Genau, als Werte zwischen 0.0 und 1.0! Das passt doch perfekt, nachdem Du schon so viel Zahlen-Karate am Zaun geübt hast. Es ist an der Zeit, Dein Wissen umzusetzen.

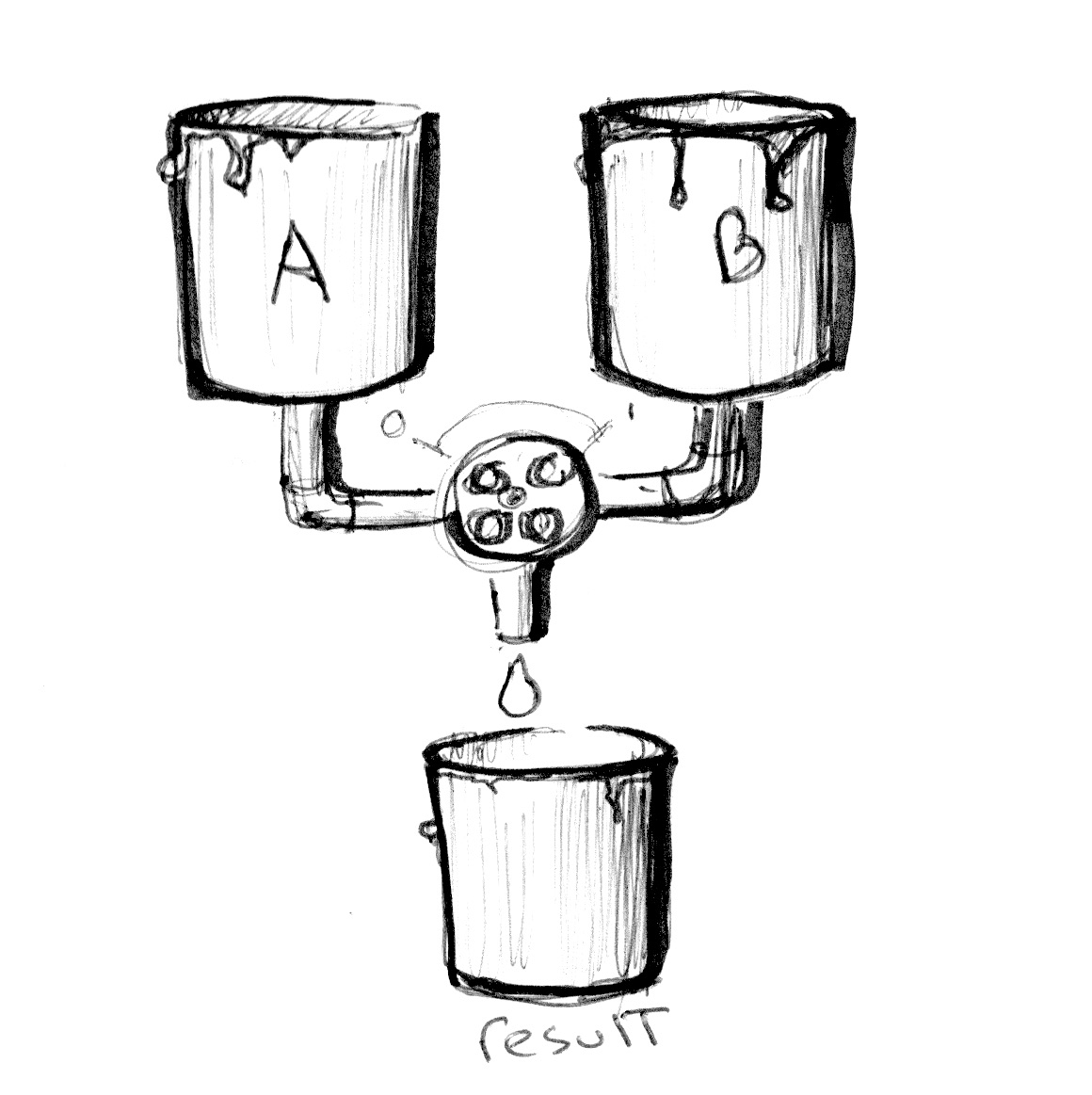
Lenke Dein Augenmerk im folgenden Programm besonders auf die Zeile 18. Schau Dir genau an, wie hier die absoluten Werte aus einer Sinusfunktion genutzt werden, um zeitabhängig und mit unterschiedlichen Verhältnissen die Farben aus den Variablen colorA und colorB zu mischen.

Jetzt zeige Deine Fähigkeiten, indem Du:

• Einen ausdrucksstarken Übergang zwischen den Farben konstruierst. Denke an ein bestimmtes Gefühl, eine impulsive menschliche Regung. Welche Farbe vermag dieses Gefühl wohl am besten auszudrücken? Und wie soll sich diese Farbe entwickeln, um anschließend wieder zu verschwinden? Animiere den Übergang mit Hilfe formgebender Funktionen. Robert Penner hat eine Reihe populärer Übergangsfunktionen für Computeranimationen entwickelt, die als easing functions bekannt sind. Du kannst für Deine Nachforschungen und als Inspiration auf dieses Beispiel zurückgreifen. Aber die besten Ergebnisse erzielst Du natürlich, wenn Du Deine ganz eigenen Übergänge kreierst.

Das Spiel mit Farbverläufen

Die mix()-Funktion hat noch mehr zu bieten. Anstelle eines einzelnen Werts vom Typ float, können wir auch einen Datentyp übergeben, der zu den ersten beiden Argumenten passt. In unserem Fall ist das ein vec3. Dadurch gewinnen wir die Kontrolle über das Mischen in allen drei Farbkanälen Rot, Grün und Blau (r, g und b).

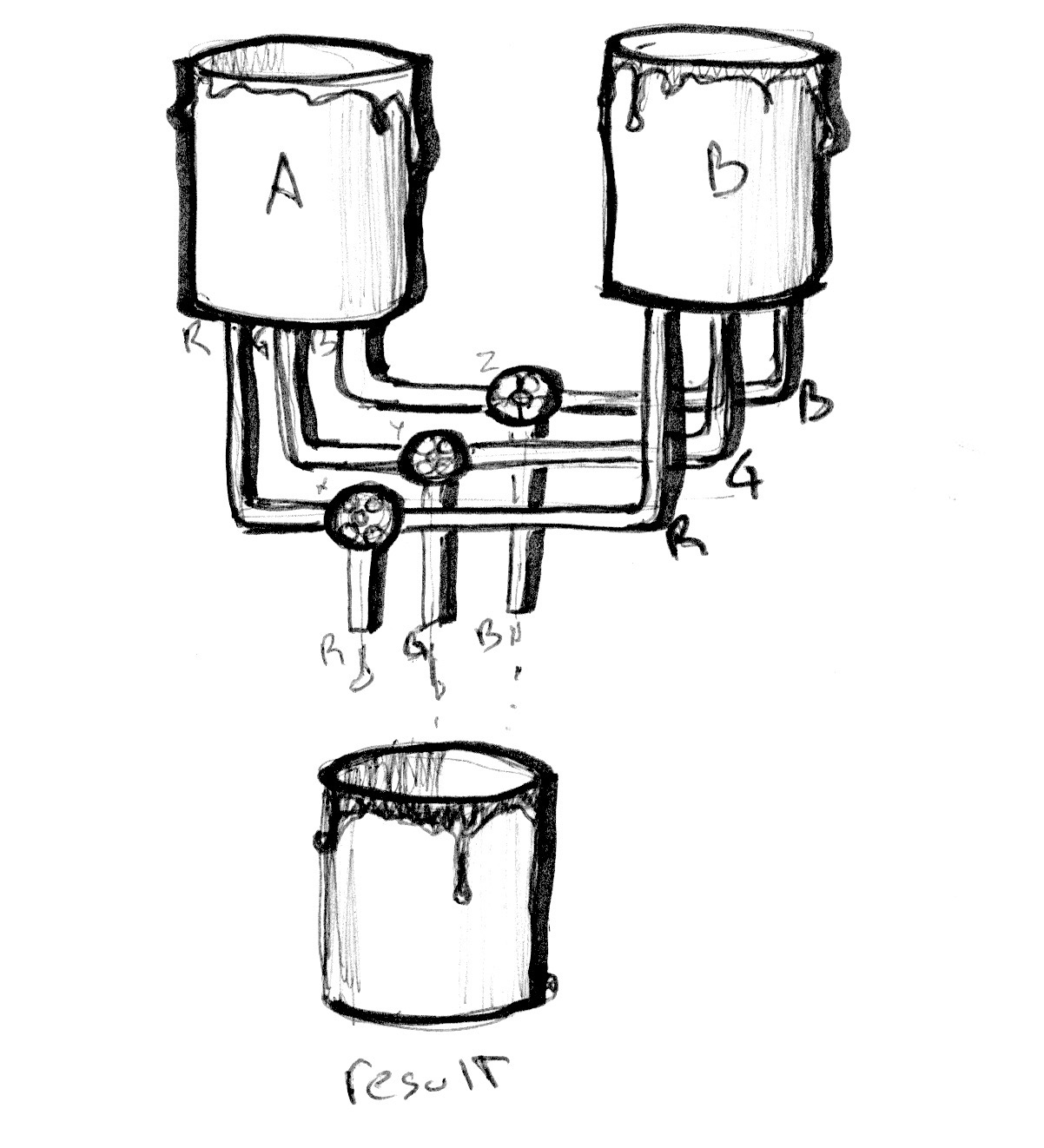
Wirf nun einen Blick auf das folgende Beispiel. Wie schon bei den Beispielen im letzten Kapitel verbinden wir den Übergang auch hier mit dem normalisierten Wert der X-Ordinate und visualisieren ihn als eine Linie. Im ersten Schritt folgen die Übergänge in allen drei Farbkanälen derselben Linie.

Lösche jetzt die Kommentarzeichen aus der Programmzeile 25, damit diese ebenfalls ausgeführt wird. Dann schau, was daraufhin geschieht. Entferne anschließend auch die Kommentarzeichen vor den Zeilen 26 und 27. Achte darauf, dass diese drei Zeilen jeweils das Mischverhältnis für die Rot-, Grün, und Blau-Kanäle zwischen den Farben aus den Variablen colorA und colorB festlegen.

Vielleicht erkennst Du die drei formgebenden Funktionen in den Zeilen 25 bis 27 wieder. Experimentiere mit ihnen. Es ist an der Zeit, dass Du die erlernten Fähigkeiten aus dem letzten Kapitel nutzt, um interessante Farbverläufe zu produzieren. Probiere die folgenden Übungen aus:

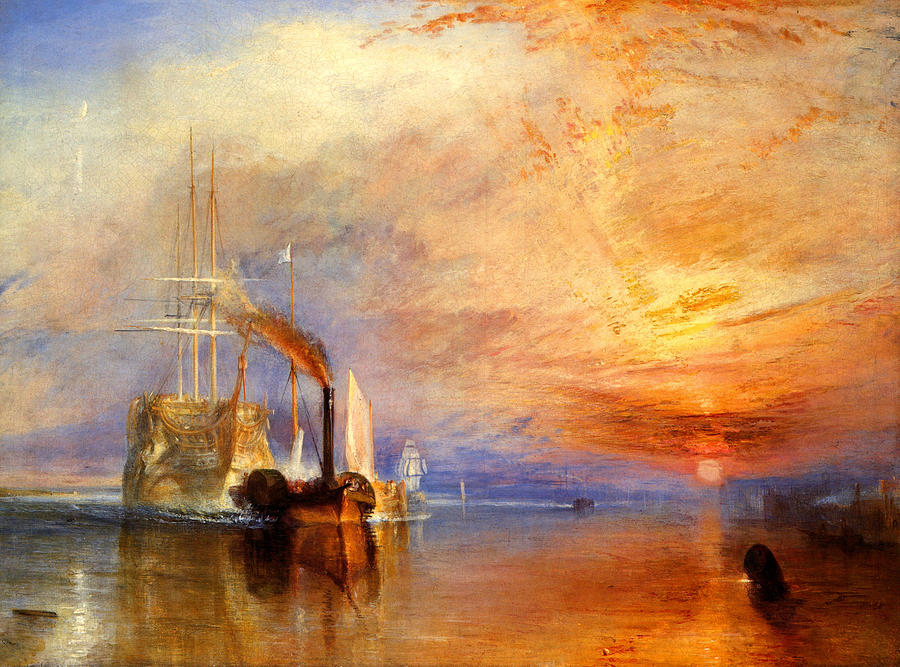
• Erzeuge einen Farbverlauf, der an den Sonnenuntergang bei William Turner erinnert.

• Animiere einen Übergang zwischen Sonnenaufgang und Sonnenuntergang mit Hilfe von u_time.

• Kannst Du mit Hilfe des bislang Erlernten einen Regenbogen entstehen lassen?

• Nutze die step()-Funktion, um eine farbenfrohe Flagge zu erzeugen.

HSB

Beim Thema „Farben“ kommen wir nicht an dem Konzept der „Farbräume“ vorbei. Wie Du vielleicht weißt, gibt es unterschiedliche Möglichkeiten, Farben zu beschreiben, jenseits ihrer Auftrennung in Rot-, Grün- und Blau-Anteile (sprich: Kanäle).

HSB steht für Hue (dt. Farbwert), Saturation (dt. Farbsättigung) und Brightness (dt. absolute Helligkeit). Dieses Farbsystem ist intuitiver und in vielen Fällen auch praktischer, wenn es um die Festlegung von Farben geht. Nimm Dir einen Moment Zeit, um die Konvertierungsfunktionen rgb2hsv() und hsv2rgb() im folgenden Programmcode zu studieren.

Indem wir die Position auf der X-Achse auf den Farbwert und die Position auf der Y-Achse auf die Helligkeit abbilden, erhalten wir ein hübsches Spektralbild. Diese räumliche Verteilung der Farben kann sehr praktisch sei, wenn es um die Auswahl einer Farbe für einen bestimmten Zweck geht.

HSB in Polarkoordinaten

Das HSB-Farbmodell wurde ursprünglich entwickelt, um Farben in Polarkoordinaten (bestehend aus einem Winkel und einem Radius) auszudrücken und nicht als kartesische Koordinaten (bestehend aus einer X- und einer Y-Ordinate). Um unsere HSB-Funktion mit Polarkoordinaten arbeiten zu lassen, müssen wir den Winkel und die Entfernung des jeweiligen Bildpunktes von der Mitte der Zeichenfläche berechnen. Dafür nutzen wir die length()-Funktion, sowie die Funktion atan(y,x) (das ist die GLSL-Variante der in vielen Programmiersprachen verfügbaren Funktion atan2(y,x) zur Berechnung des Arkustangens).

Bei der Nutzung von Vektor- und Trigonometrie-Funktionen werden Variablen der Datentypen vec2, vec3 und vec4 wie Vektoren behandelt, auch wenn sie tatsächlich Farben verkörpern. Wir beginnen hier also, Farben und Vektoren gleichermaßen zu bearbeiten - eine Flexibilität, die sich noch als äußerst praktisch und weitreichend erweisen wird.

Hinweis: Nur, falls Du Dich fragst: Abgesehen von length gibt es noch viele weitere geometrische Funktionen. Dazu gehören beisielsweise: distance(), dot(), cross, normalize(), faceforward(), reflect() und refract().

Außerdem bietet GLSL vergleichende Funktionen für Vektoren wie lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() und notEqual().

Nachdem wir den Winkel und die Entfernung (Länge) berechnet haben, müssen wir diese Werte normalisieren, indem wir sie auf den Wertebereich zwischen 0.0 und 1.0 abbilden. In der Programmzeile 27 liefert der Aufruf von atan(y,x) den Winkel als Bogenmaß zwischen -PI und PI (-3.14 bis 3.14) zurück. Deshalb müssen wir dieses Ergebnis durch TWO_PI (Zweimal PI, als Konstante oben im Programm definiert) teilen. Wir erhalten dadurch Werte zwischen -0.5 und 0.5, die wir durch einfache Addition von 0.5 auf den benötigten Wertebereich zwischen 0.0 und 1.0 abbilden. Allerdings werden wir hier als Ergebnis immer maximal 0.5 erhalten, weil wir ja die Entfernung von der Mitte der Zeichenfläche berechnen. Deshalb müssen wir dieses Ergebnis noch mit 2 multiplizieren, damit wir maximal auf den Wert von 1.0 kommen.

Wie Du siehst, dreht sich also auch hier das ganze Spiel darum, Werte zwischen 0.0 und 1.0 zu erzielen, mit denen wir so gerne arbeiten.

Probiere die folgenden Übungen aus:

• Verändere das obige Programmbeispiel so, dass sich das Farbrad dreht, wie der Mauszeiger bei einer länger währenden Operation.

• Nutze eine formgebende Funktion in Verbindung mit der Konvertierungsfunktion von HSB nach RGB, um einen bestimmten Farbwert in den Vordergrund zu rücken und die anderen Farben „klein“ zu halten.

• Wenn Du Dir das Farbrad auf Farbauswahlfeldern (wie in der folgenden Abbildung) genau anschaust, erkennst Du, dass diese einen RYB-Farbraum repräsentieren. Die gegenüberliegende Farbe von Rot sollte z.B. Grün sein, doch in unserem obigen Beispielprogramm erscheint dort Zyan. Gelingt es Dir, einen Weg zu finden, damit unser Beispielprogramm das gleiche Farbbild liefert, wie auf der Abbildung unten? (Ein Tipp: Das ist der perfekte Moment, um eine passende formgebende Funktion zum Einsatz zu bringen.)

• Lies Josef Albers Buch: „Interaction of Color“ und klicke die folgenden Shader an, um aus deren Programmcode zu lernen.

Ein Hinweis zu Funktionen und ihren Argumenten

Bevor wir zum nächsten Kapitel springen, lass und kurz innehalten und einen Schritt zurückgehen. Schau Dir noch einmal die Funktionen aus den letzten Beispielprogrammen an. Vielleicht fällt Dir das Schüsselwort in im Kopf einer Funktion vor dem jeweiligen Argument auf. Es handelt sich dabei um einen sogenannten qualifier, der in diesem Fall festlegt, dass der jeweilige Parameter von der Funktion nur ausgelesen und nicht überschrieben werden kann. In kommenden Programmbeispielen werden wir sehen, dass Parameter auch als out oder inout gekennzeichnet werden können. inout entspricht dabei der Übergabe eines Arguments „by reference“, so dass Änderungen an diesem Parameter auch an den Aufrufer und in die von ihm eingesetzte Variable zurückfließen.

int newFunction(in vec4 aVec4,   // nur auslesbar
                out vec3 aVec3,  // nicht initalisiert, nur beschreibbar
                inout int aInt); // lesen und schreiben, Aenderungen fliessen zum Aufrufer zurueck

Du hast vielleicht nicht damit gerechnet, aber jetzt haben wir bereits alle Elemente beisammen, um aufregende Grafiken zu erstellen. Im nächsten Kapitel werden wir lernen, wie man alle unsere kleinen Tricks nutzen kann, um den Raum richtig in Wallung zu bringen. Ja, du hast richtig gehört. Genau darum geht's.