Colores
No hemos tenido oportunidad todavía de hablar sobre los tipos de vectores en GLSL. Antes de ir más lejos, es importante entender cómo funcionan estas variables, hablar de colores es una buena forma de entenderlos.
Si te encuentras familiarizado con la programación orientada a objetos, probablemente te habrás dado cuenta que estamos accediendo a los valores de los vectores, como si fuese un struct de C.
vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;Definir los colores usando x, y y z puede ser muy confuso y engañoso. Es por eso que hay otras formas de acceder a esos valores, con nombres diferentes. Los valores de .x, .y y .z, se pueden llamar también .r, .g y .b, o también .s, .t y .p (.s, .t y .p son usados para coordenadas espaciales de texturas, lo veremos en otro capítulo). También podemos acceder a un valor de los vectores, usando índices de posición,[0], [1] y [2].
En las siguientes lineas puedes ver todas las formas de acceder al mismo valor.
vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;Las diferentes formas de acceder a las variables son sólo nomenclaturas diseñadas para que el código sea más claro. Esta flexibilidad de los shaders, es una puerta de entrada para poder relacionar el color con las coordenadas en el espacio.
Otra estupenda funcionalidad de los vectores en GLSL, es que las propiedades se pueden combinar en el orden que quieras, lo que hace muy sencillo manipular y mezclar valores. Esta habilidad es conocida como swizzle.
vec3 yellow, magenta, green;
// Making Yellow
yellow.rg = vec2(1.0); // Assigning 1. to red and green channels
yellow[2] = 0.0; // Assigning 0. to blue channel
// Making Magenta
magenta = yellow.rbg; // Assign the channels with green and blue swapped
// Making Green
green.rgb = yellow.bgb; // Assign the blue channel of Yellow (0) to red and blue channelsMezclando color
Ahora que sabes como se definen los colores, es hora de integrar esto con lo que aprendimos previamente. En GLSL hay una función muy útil, mix(), que te permite mezclar dos valores en porcentaje. ¿Puedes adivinar cuál es el rango de porcentaje? ¡Si, valores de 0.0 a 1.0! Lo cual es perfecto para ti, porque luego de esas largas horas practicando tus movimientos de karate en la cerca. ¡Ahora es el momento de usar esos conocimientos!
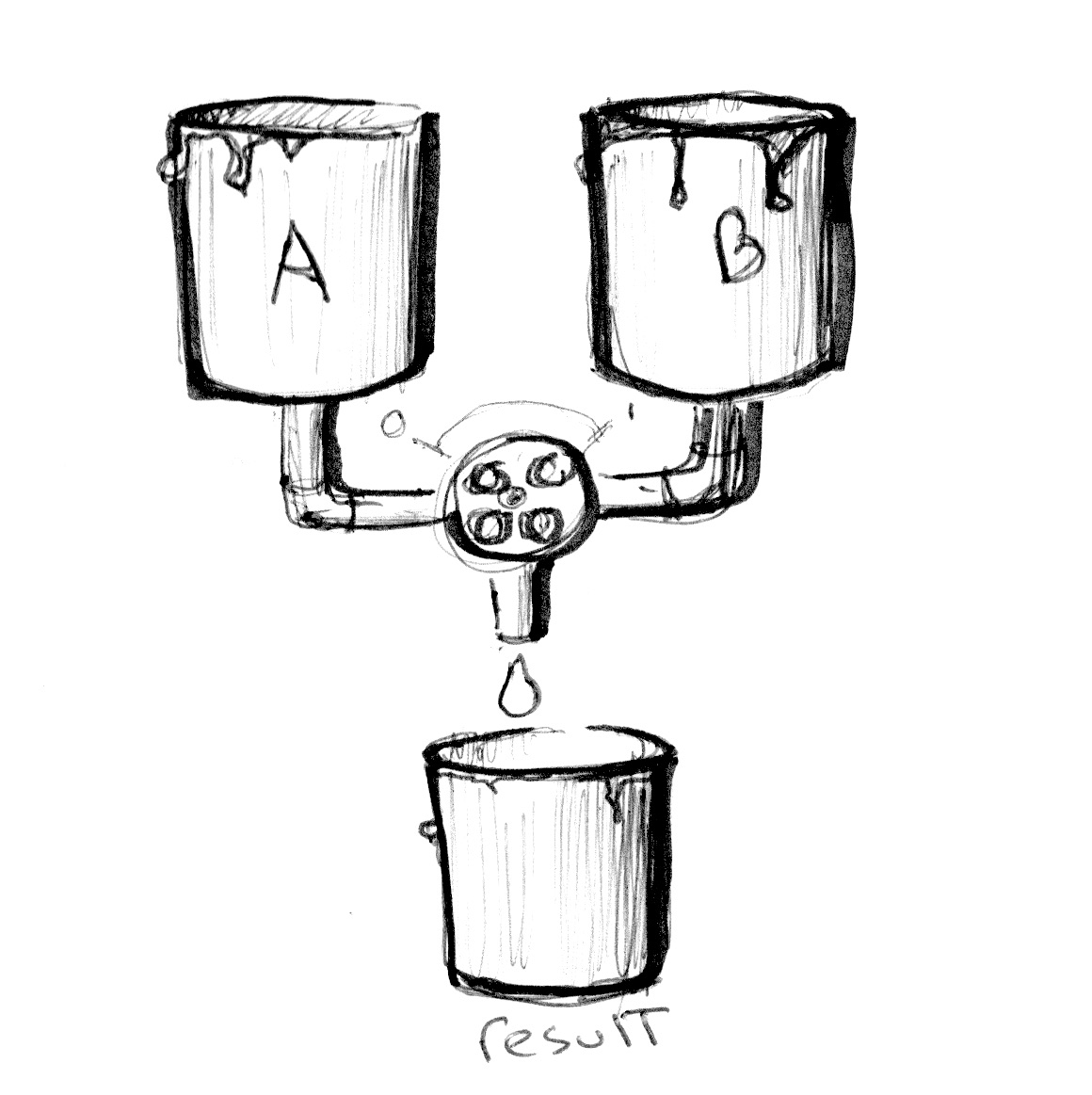
Echa un vistazo al siguiente código en la línea 18 y observa cómo estamos usando los valores absolutos de una onda sinusoidal para mezclar colorA y colorB.
Demuestra tus habilidades:
- Crea una transición expresiva entre dos colores. Piensa en una emoción en particular. ¿Qué color es el más representativo de esa emoción? ¿Cómo aparece? ¿Cómo se desvanece? Piensa en otra emoción y el color que la represente. Cambia los colores del código de arriba por los de tus emociones. Luego anima las transiciones utilizando las funciones de forma. Robert Penner desarrolló una serie de funciones de forma populares, conocidas como easing functions, puedes usar este ejemplo como investigación o inspiración, pero los mejores resultados saldrán cuando crees tus propias transiciones.
Jugando con gradientes
La función mix() tiene mucho para ofrecer. En vez de usar un sólo float, podemos pasarle variables en los dos primeros argumentos, en nuestro caso un vec3. Haciendo esto podemos controlar los porcentajes de cada canal de color, r, g y b.
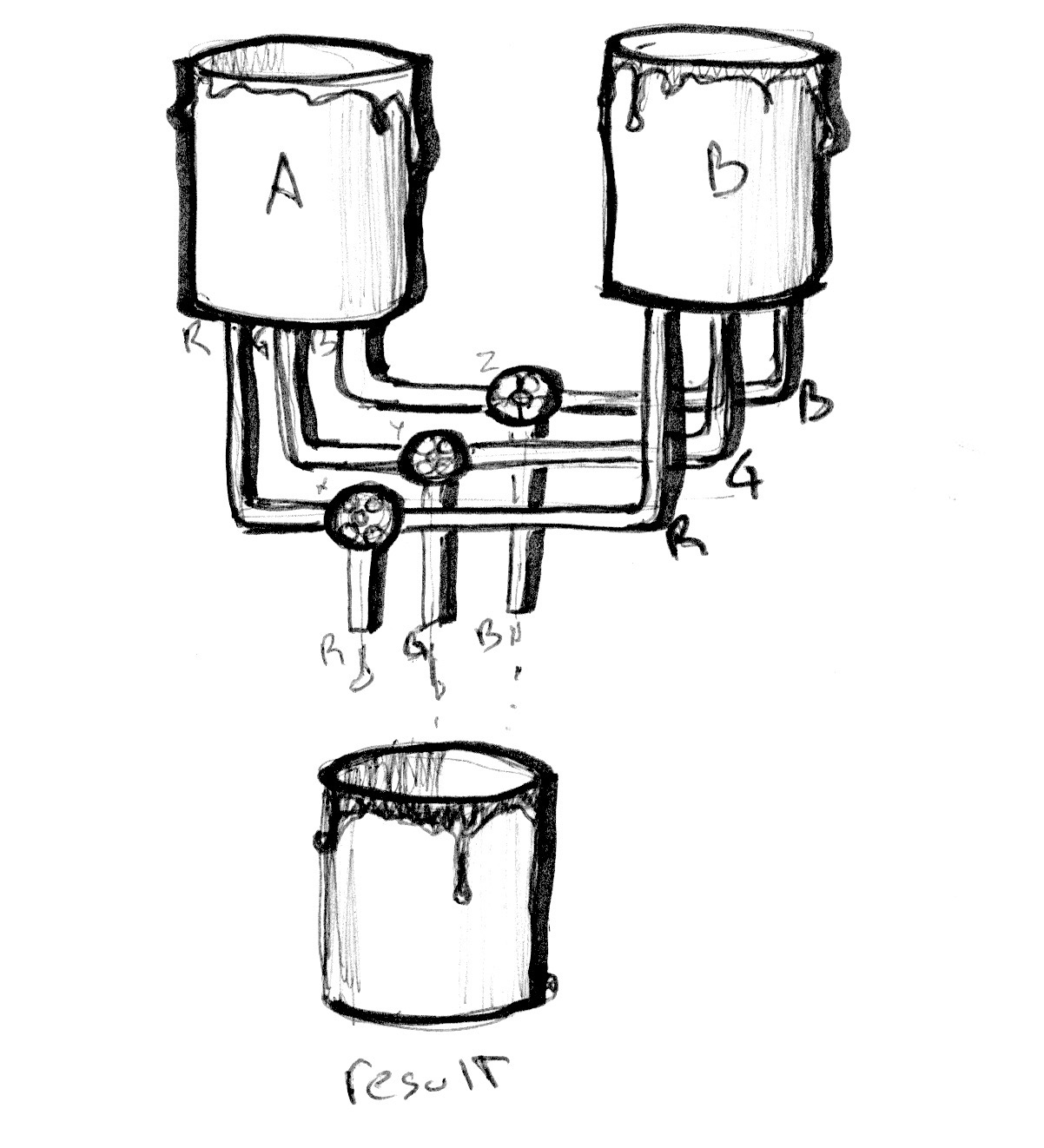
Mira el siguiente ejemplo, como en los del capítulo anterior, estamos conectando la transición normalizada de la coordenada x y visualizándola con una línea. Ahora todos los canales van por la misma línea.
Ahora descomenta la línea 25 y mira lo que sucede. Luego descomenta las líneas 26 y 27. Recuerda que con las líneas visualizamos la cantidad de colorA y colorB a mezclar por cada canal.
Probablemente reconoces las tres funciones de forma que usamos en las líneas 25 y 27. ¡Juega con ellas! Es hora de mezclar y explorar lo aprendido en el capítulo previo para crear gradientes interesantes. Prueba hacer los próximos ejercicios:
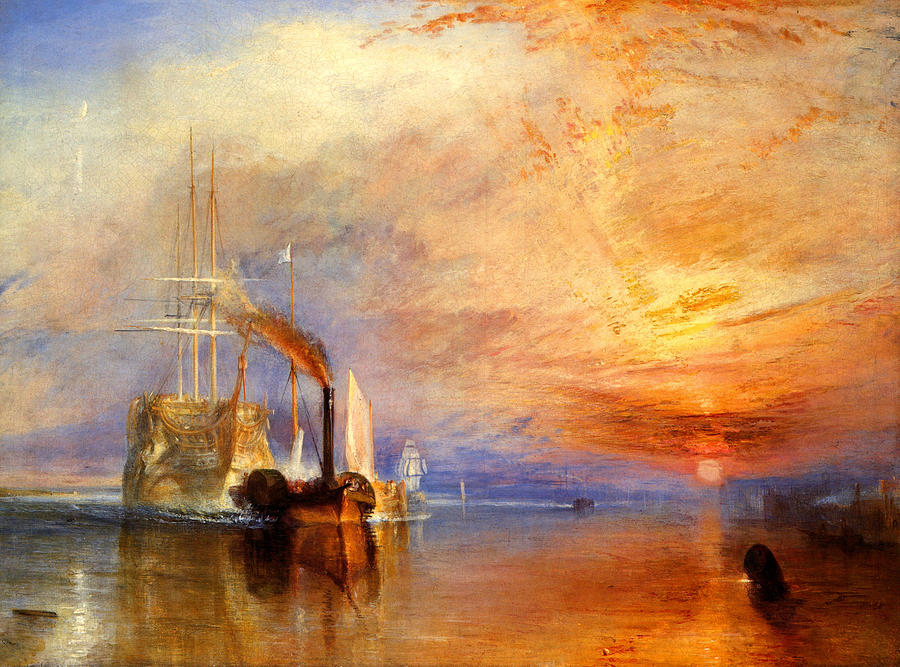
-
Crea un gradiente que se parezca a un atardecer de William Turner.
-
Crea una transición entre el atardecer y el amanecer usando
u_time. -
¿Puedes crear un arcoíris con lo que hemos aprendido hasta ahora?
- Usa la función
step()para crear una bandera colorida.
HSB
No podemos hablar de color sin mencionar el espacio de color. Probablemente sabes que hay diferentes formas de organizar un color más allá de usar los canales de rojo, verde y azul.
HSB significa Hue (tono), Saturation (saturación) y Brightness (brillo o valor), es una forma útil y más intuitiva de organizar el color. Tomate un momento para leer las funciones rgb2hsv() y hsv2rgb() del código siguiente.
Conectando la posición del eje x al tono y la posición del eje y al brillo podemos obtener este bonito espectro del color visible. La distribución espacial del color puede sernos muy útil; es más intuitivo seleccionar un color usando HSB que con RGB.
HSB en coordenadas polares
HSB fue originalmente diseñado para ser representado en coordenadas polares (basadas en el ángulo y el radio) en vez de coordenadas cartesianas (basadas en x e y). Para asociar nuestra función HSB a coordenadas polares necesitamos obtener el ángulo y la distancia del centro de la ventana. Para hacer eso usaremos la función length() y atan(y,x) (que es la versión en GLSL del comunmente usado atan2(y,x)).
Cuando usamos vectores y funciones trigonométricas, vec2, vec3 y vec4 son tratados como vectores, incluso cuando representan colores. Comenzaremos a tratar a los colores y a los vectores de una manera similar, de hecho te darás cuenta que es un concepto muy poderoso y flexible.
Nota: Si te preguntabas si había más funciones geométricas además de length: distance(), dot(), cross, normalize(), faceforward(), reflect() y refract(). También GLSL tiene funciones relacionadas a los vectores como: lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() y notEqual().
Una vez que obtenemos el ángulo y la longitud, necesitamos "normalizar" sus valores al rango de 0.0 a 1.0. En la línea 27, atan(y,x) devolverá el angulo en radianes entre -PI y PI (-3.14 a 3.14), por lo que necesitamos dividir este número por TWO_PI (declarado arriba en nuestro código) para obtener valores de -0.5 a 0.5, que con una simple suma podemos transformar al rango deseado de 0.0 a 1.0. El radio devolverá un máximo de 0.5 (porque estamos calculando la distancia desde el centro del viewport) por lo tanto necesitamos duplicar este rango (multiplicándolo por dos) para obtener un máximo de 1.0.
Como podrás notar, todo se trata de transformar y manipular rangos de 0.0 a 1.0.
Intenta resolver los próximos ejercicios:
-
Modifica el ejemplo polar, para obtener una rueda que gire, como el ícono de cargando.
- Usa una función de forma junto con la conversión de HSB a RGB para expandir un color en particular y encoger el resto.

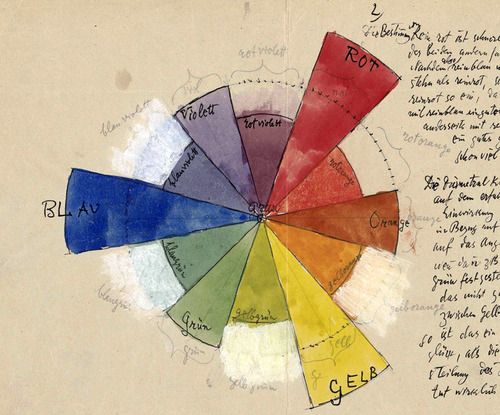
- Si miras detenidamente el círculo cromático usado en los goteros de color (ver la imagen de abajo), usan un espectro diferente, se trata del RYB. Por ejemplo, el opuesto del color rojo, debería ser el verde, pero en nuestro ejemplo es el cyan. ¿Podrías encontrar la forma de igualarlo para que luzca igual a la siguiente imagen? [Pista: este es un buen momento para usar funciones de forma.]

Nota acerca de las funciones y los argumentos
Antes de saltar al próximo capítulo, detengámosnos y retrocedamos. Volvamos a ver las funciones en los ejemplos previos. Notaras el in antes del tipo de argumento. Este es un qualifier y en este caso indica que la variable es de solo lectura. En ejemplos futuros veremos que es posible definir argumentos como out o inout. Este último, inout, es conceptualmente similar a pasar un argumento por referencia, lo que nos da la posibilidad de modificar la variable pasada.
int newFunction(in vec4 aVec4, // read-only
out vec3 aVec3, // write-only
inout int aInt); // read-writeSeguramente no me crees, pero ya tenemos todos los elementos necesarios para crear dibujos geniales. En el próximo capítulo aprenderemos a combinar todos nuestros trucos para crear formas geométricas mezclando el espacio. Si... mezclando el espacio.