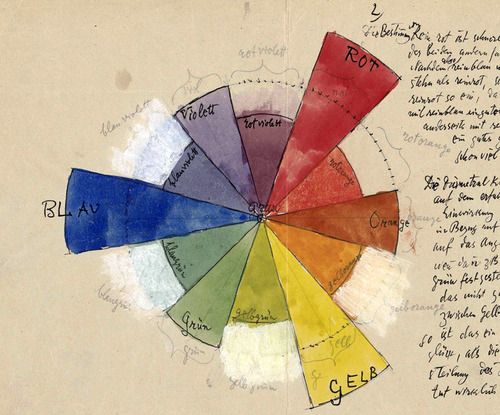
Colori

Non abbiamo ancora avuto occasione di parlare dei tipi di vettore in GLSL. Prima di andare avanti, è importante imparare meglio come funzionano queste variabili e parlare di colori è un buon modo per capirle meglio.

Se siete pratici con i paradigmi di programmazione orientata agli oggetti, probabilmente avrete notato che stiamo accedendo ai dati interni ai vettori, come se fossero una qualunque struct di C.

vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

Definire il colore usando una notazione x, y e z può essere fuorviante e creare confusione, vero? Per questo esistono altri modi di accedere alle stesse informazioni, con nomi diversi. I valori di .x, .y e .z possono anche essere chiamati .r, .g e .b, e .s, .t e .p. (.s, .t e .p solitamente sono usati per le coordinate spaziali di una texture, che vedremo nel prossimo capitolo). Puoi anche accedere ai valori in un vettore usando gli indici di posizione [0], [1] e [2].

Le righe seguenti mostrano tutti i modi per accedere agli stessi valori:

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

Questi diversi modi di indicare le variabili all’interno di un vettore sono solo nomenclature progettate per aiutarvi nella scrittura di un codice chiaro. Tale flessibilità incorporata nel linguaggio shading è una porta per iniziare a pensare all’intercambiabilità tra colore e coordinate spaziali.

Un’altra grandiosa caratteristica dei tipi di vettore in GLSL è che le proprietà possono essere combinate in qualsiasi ordine voi vogliate, e ciò rende più facile manipolare e mescolare i valori. Quest’abilità è chiamata swizzle.

vec3 yellow, magenta, green;

// Per creare il giallo
yellow.rg = vec2(1.0);  // Assegnare 1. ai canali del rosso e del verde
yellow[2] = 0.0;        // Assegnare 0. al canale del blu

// Per fare il magenta
magenta = yellow.rbg;   // Invertite il canale del verde con quello del blu

// Per ottenere il verde
green.rgb = yellow.bgb; // Assegnare il canale blu del giallo (0) ai canali rosso e blu

Mescolare i colori

Ora che sapete come sono definiti i colori, è tempo di integrare ciò con le nostre conoscenze precedenti. In GLSL c’è una funzione molto utile, mix(), che vi permette di mescolare due valori in percentuali. Riuscite ad indovinare l’estensione della percentuale? Esatto, i valori tra 0.0 e 1.0! Dopo lunghe ore di esercizio, finalmente è ora di mettere le vostre conoscenze in pratica!

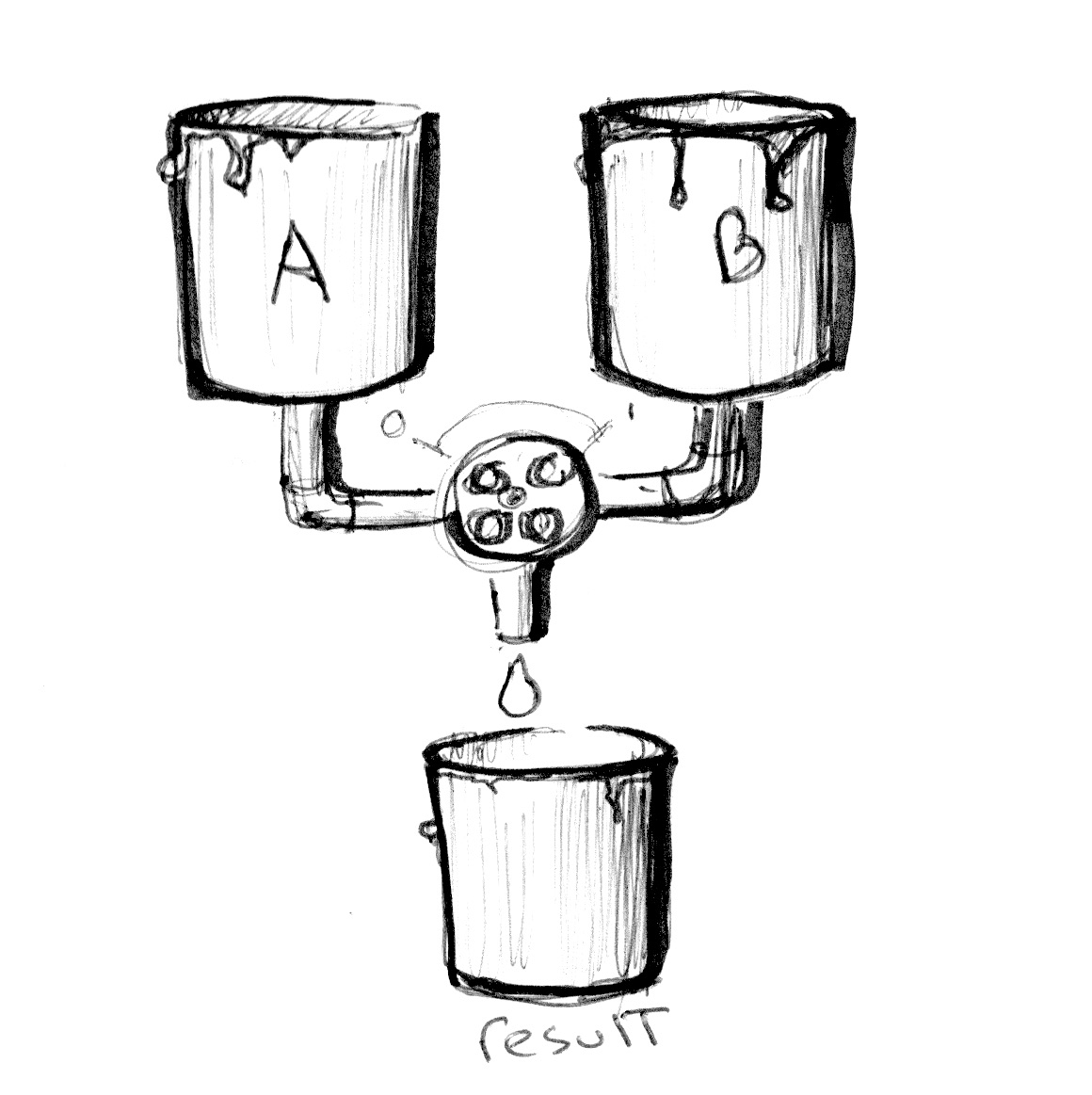
Guardate il codice seguente alla riga 18 e osservate come stiamo usando i valori assoluti di un’onda sinusoidale nel tempo per mescolare colorA e colorB.

Mettete in risalto le vostre capacità:

• Create una transizione espressiva tra colori. Pensate a un’emozione particolare. Quale colore la rappresenta meglio? Come appare? Come si dissolve? Pensate ad un’altra emozione e al colore corrispondente. Cambiate il colore iniziale e finale del codice soprastante per ricreare quelle emozioni. Poi animate la transizione usando le funzioni di forma. Robert Penner ha sviluppato una serie di funzioni di forma famose per animazioni al computer, note come easing functions. Potete usare quest’esempio come ricerca ed ispirazione ma il risultato migliore sarà ottenuto facendo le vostre transizioni.

Giocare con i gradienti

La funzione mix() ha molto da offrire. Invece di usare un solo float, possiamo passare un tipo di variabile che abbina i primi due argomenti, nel nostro caso un vec3. Facendo così, possiamo controllare le percentuali di ciascun canale colore r, g e b.

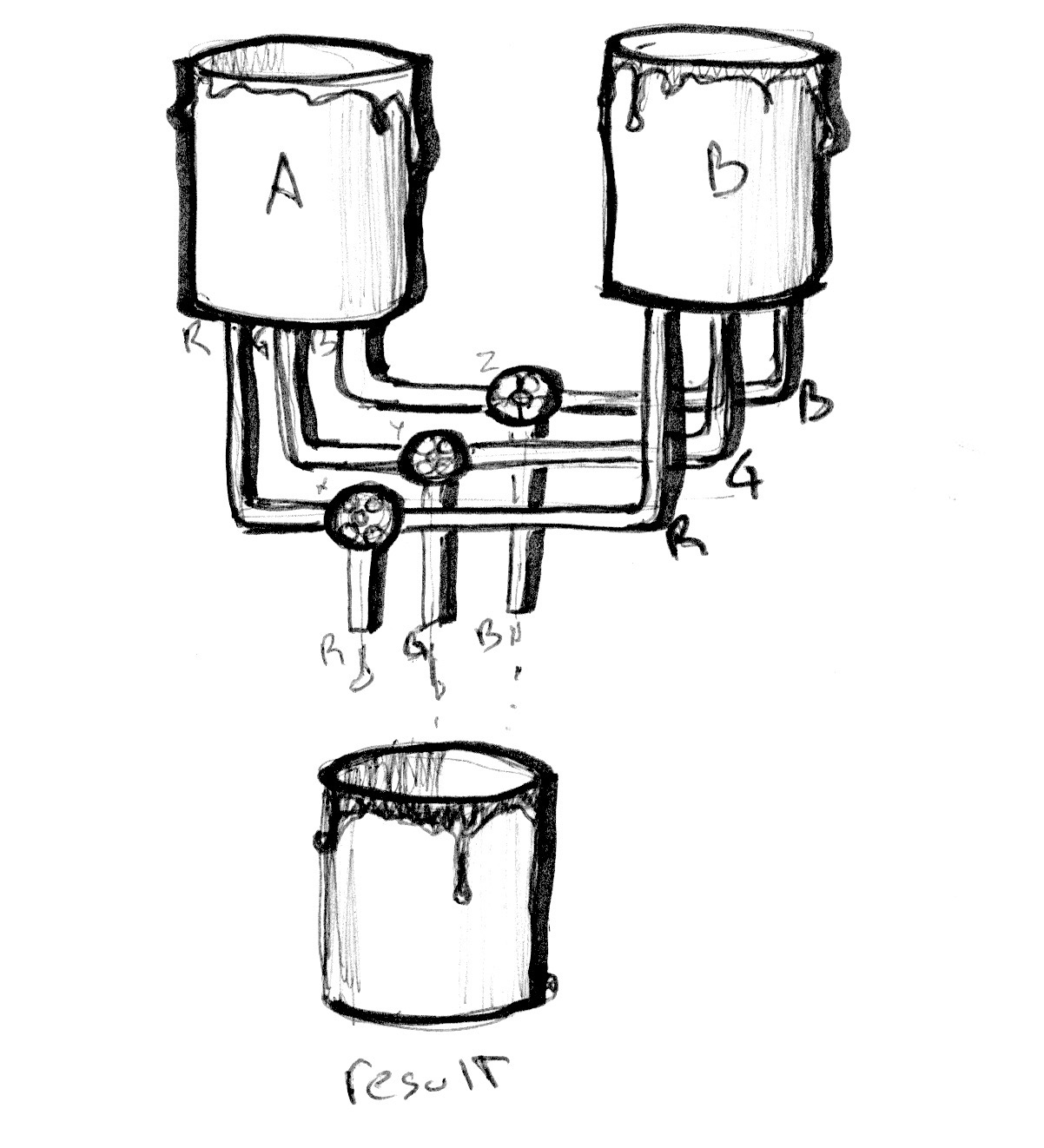
Guardate l'esempio seguente. Così come negli esempi nel capitolo precedente, stiamo collegando la transizione alla x normalizzata e la visualizziamo con una linea. In questo momento tutti e tre i canali seguono la medesima linea.

Ora, togliete il commento alla riga 25 e guardate cosa succede. Poi provate a togliere il commento alle righe 26 e 27. Ricordate che le linee visualizzano la quantità di colorA e colorB da mescolare per ogni canale.

Probabilmente riconoscerete le tre funzioni di forma che stiamo usando dalla riga 25 alla 27. Giocate con queste! È il momento per esplorare e mostrare le vostre abilità acquisite nel capitolo precedente e creare gradienti interessanti. Provate i seguenti esercizi:

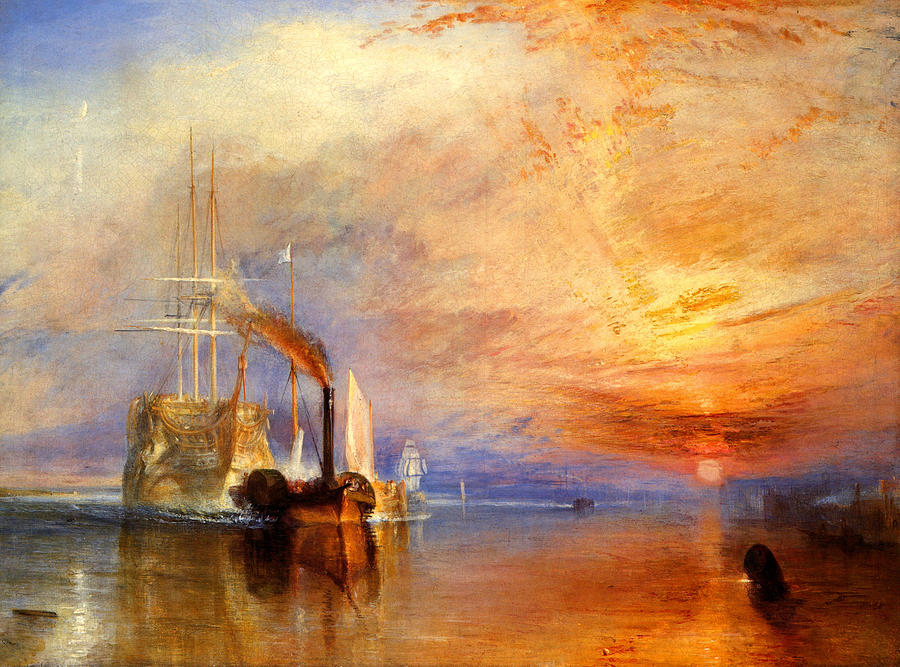
• Create un gradiente che assomigli al tramonto di William Turner.

• Animate una transizione tra un'alba e un tramonto usando u_time.

• Riuscite a creare un arcobaleno usando ciò che abbiamo imparato fino ad ora?

• Usate la funzione step() per creare una bandiera variopinta.

HSB

Non possiamo parlare di colore senza menzionare lo spazio di colore. Come probabilmente saprete, ci sono diversi modi di organizzare il colore, oltre ai canali del rosso, verde e blu.

HSB sta per Hue (Tonalità), Saturation (Saturazione) e Brightness (Luminosità o Valore) ed è un modo di organizzare i colori più intuitivo e utile. Prendete un momento per leggere le funzioni rgb2hsv() e hsv2rgb() nel codice seguente.

Mappando la posizione sull'asse x con la tonalità e la posizione sull'asse y con la luminosità, otteniamo uno spettro dei colori visibili. Questa distribuzione spaziale del colore può essere molto pratica; è più intuitivo selezionare un colore con HSB che con RGB.

HSB nelle coordinate polari

Originariamente HSB è stato creato per essere rappresentato in coordinate polari (basate su angoli e raggio) e non in coordinate cartesiane (basate su x e y). Per unire la nostra funzione HSB alle coordinate polari, dobbiamo ottenere l'angolo e la distanza dal centro del canvas per ogni coordinata pixel. Per far questo usiamo la funzione length() e atan(y,x) (che è la versione GLSL della più comune atan2(y,x)).

Quando si usano vettori e funzioni trigonometriche, vec2, vec3 e vec4 sono considerati come vettori anche quando rappresentano i colori. Inizieremo a considerare in modo simile i colori e i vettori, e in realtà troverete che questa flessibilità concettuale è molto potente.

Nota: se ve lo stavate chiedendo, esistono altre funzioni geometriche oltre a length, come: distance(), dot(), cross, normalize(), faceforward(), reflect() e refract(). Anche GLSL ha speciali funzioni vettoriali come: lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() e notEqual().

Una volta che otteniamo l'angolo e la lunghezza dobbiamo "normalizzare" i loro valori in una scala tra 0.0 e 1.0. alla riga 27, atan(y,x) restituirà un angolo in radianti tra –PI e PI (-3.14 e 3.14), quindi dobbiamo dividere questo numero per TWO_PI (definito nella parte superiore del codice) per ottenere valori tra -0.5 e 0.5, che con una semplice addizione cambiamo nella scala desiderata tra 0.0 e 1.0. Il raggio restituirà un massimo di 0.5 (perché stiamo calcolando la distanza dal centro del punto di osservazione), quindi abbiamo bisogno di raddoppiare questa distanza (moltiplicando per due) per ottenere un massimo di 1.0.

Come potete vedere, il nostro gioco qui riguarda semplicemente il trasformare e manipolare le distanze tra 0.0 e 1.0.

Provate gli esercizi successivi:

• Modificate l'esempio polare per ottenere una ruota di colori che gira, proprio come l'icona del mouse che indica il caricamento.

• Usate una funzione di forma unita alla funzione di conversione da HSB a RGB per espandere un particolare valore di tonalità e comprimere il resto.

• Se guardate da vicino la ruota cromatica usata dai selettori del colore (guardate l'immagine qui sotto), essi usano uno spettro diverso da quello dello spazio di colore RYB. Per esempio, il colore opposto al rosso dovrebbe essere il verde, ma nel nostro esempio è il ciano. Riuscite a trovare un modo per rimediare e far sì che sembri esattamente l'immagine seguente? [Suggerimento: è un buon momento per usare le funzioni di forma].

• Leggete il libro di Josef Albers "L'interazione dei colori” e usate i seguenti esempi di shader come pratica.

Nota sulle funzioni e sugli argomenti.

Prima di addentrarci nel capitolo successivo, fermiamoci e torniamo indietro. Osservate le funzioni negli esempi precedenti. Noterete un in prima di definire il tipo degli argomenti. Questo è un qualificatore e in questo caso specifica che la variabile è solamente letta. Negli esempi futuri vedremo che è anche possibile definire argomenti come out o inout. Quest'ultimo, inout, è concettualmente simile a passare un argomento per referenza, il che ci dà la possibilità di modificare una variabile passata.

int newFunction(in vec4 aVec4,   // solo lettura
                out vec3 aVec3,    // solo scritture
                inout int aInt);   // lettura e scrittura

Potreste non crederci ma ora abbiamo tutti gli elementi per creare dei fantastici disegni. Nel prossimo capitolo impareremo come si possono combinare tutte queste tecniche per creare forme geometriche fondendo lo spazio. Sì, avete capito bene, fondendo lo spazio.