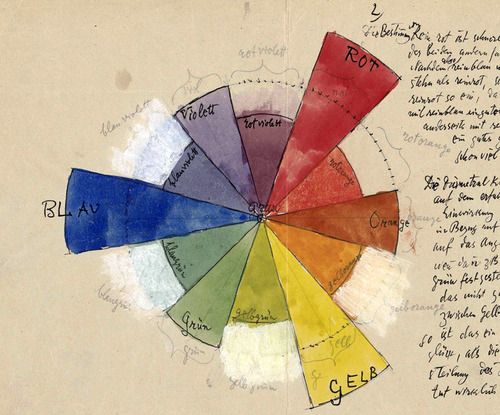
Цвета
Ранее мы не очень подробно раскрывали тему работы с векторами в GLSL. Прежде чем двинуться дальше, не помешает изучить векторы поглубже, и работа с цветом как нельзя лучше подходит для этого.
Если вы знакомы с объектно-ориентированной парадигмой программирования, вы скорее всего заметили, что мы обращаемся к данным в векторах на манер структур (struct) в языке С.
vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;Работа с цветом через x, y и z может сбить с толку и ввести в заблуждение, не так ли? Поэтому в GLSL можно получить доступ к тем же самым данным через другие имена. Значения .x, .y и .z так же именуются .r, .g и .b, и .s, .t и .p. Последний набор имён обычно используется для пространственных координат текстур, с которыми мы познакомимся в следующих главах. Кроме того, для доступа к элементам вектора можно использовать численные индексы [0], [1] и [2].
Следующие строки демонстрируют все способы доступа к одним и тем же данным:
vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;Все эти способы - всего лишь дополнительные имена для доступа к одним и тем же данным, которые призваны помочь вам в создании более понятного кода. Эта гибкость языка шейдеров станет путеводной нитью, помогающей вам мыслить о значениях цвета и координатах пространства как о взаимозаменяемых сущностях.
Другое замечательное свойство векторных типов GLSL - это возможность доступа к координатам в произвольном порядке, которая упрощает преобразование и смешивание значений.
vec3 yellow, magenta, green;
// Задаём жёлтый цвет
yellow.rg = vec2(1.0); // Записываем 1.0 в красный и зелёный каналы
yellow[2] = 0.0; // Записываем 0.0 в синий
// Задаём малиновый цвет
magenta = yellow.rbg; // Меняем местами зелёный и синий
// Задаём зелёный цвет
green.rgb = yellow.bgb; // Записываем значение синего канала жёлтого цвета (0) в красный и синийСмешивание цветов
Теперь, когда вы знаете как задаются цвета, мы можем собрать все новые знания воедино. В GLSL есть очень полезная функция mix(), которая смешивает значения в указанной пропорции. Угадайте, как задаются пропорции? Конечно же, числом от 0.0 до 1.0! И это просто отлично, учитывая те долгие часы, что вы практиковали движения карате с забором. Самое время применить их на практике!
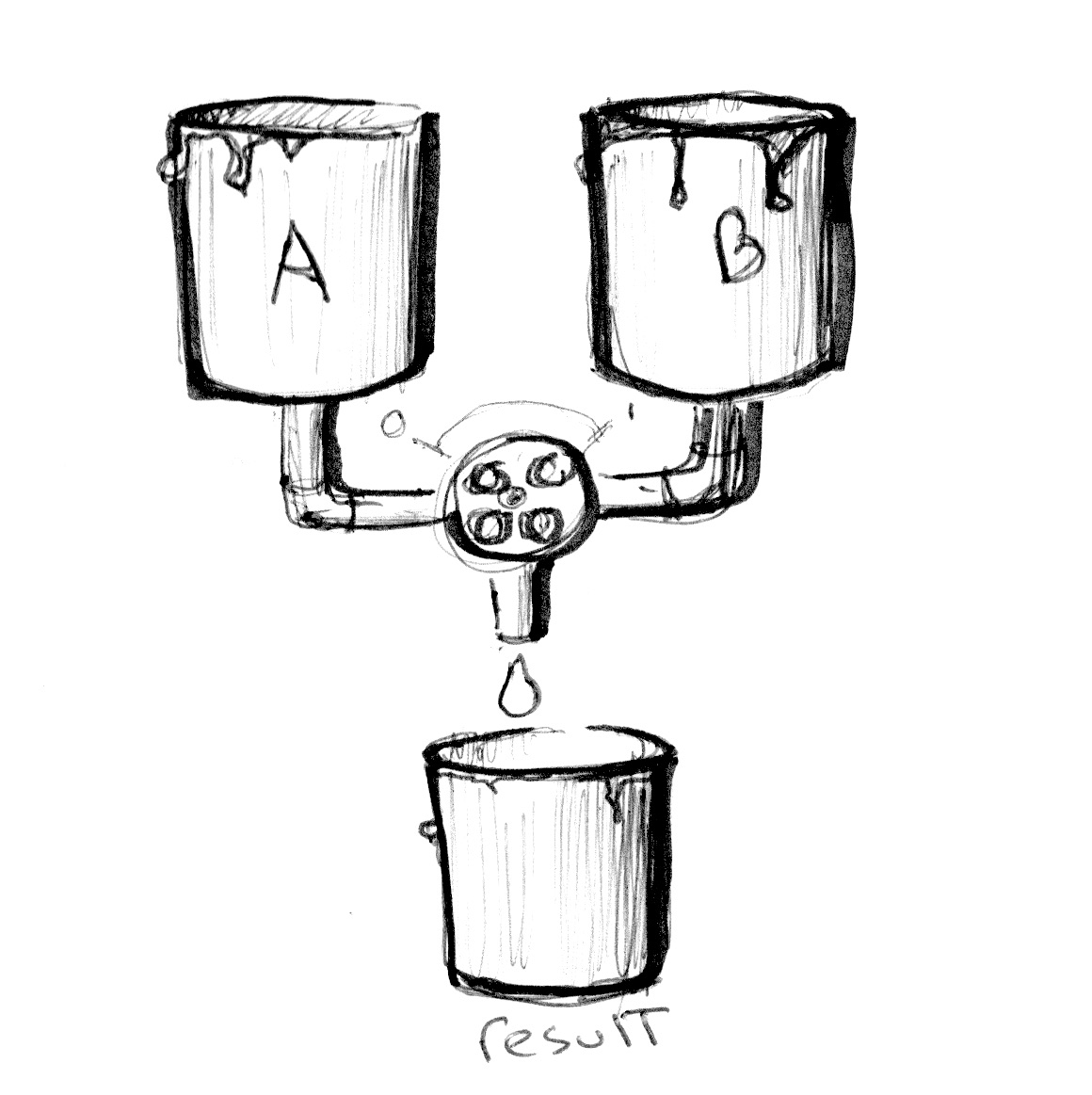
В строке 18 в следующем куске кода мы используем абсолютное значение синуса от времени для смешивания цветов A и B.
Покажите, что вы можете:
- Создайте экспрессивный переход между цветами. Вообразите какую-нибудь эмоцию. Какой цвет больше всего ассоциируется с ней? Как она появляется? Как она сходит на нет? Придумайте другую эмоцию и подходящий для неё цвет. Поменяйте начальный и конечный цвета в коде выше в соответствии с этими эмоциями. Анимируйте переход с помощью функций формы. Роберт Пеннер разработал набор популярных функций для компьютерной анимации, известный под названием упрощающих функций. Вы можете использовать этот пример для исследования и поиска вдохновения, но вы сможете достигнуть наилучшего результата только создав собственные функции перехода.
Играемся с градиентами
Функция mix() способна на большее. Вместо одного числа с плавающей точкой мы можем передать переменную того же типа, что и первые два аргумента (vec3 в нашем случае). Таким образом мы можем управлять пропорциями каждого канала r, g и b по отдельности.
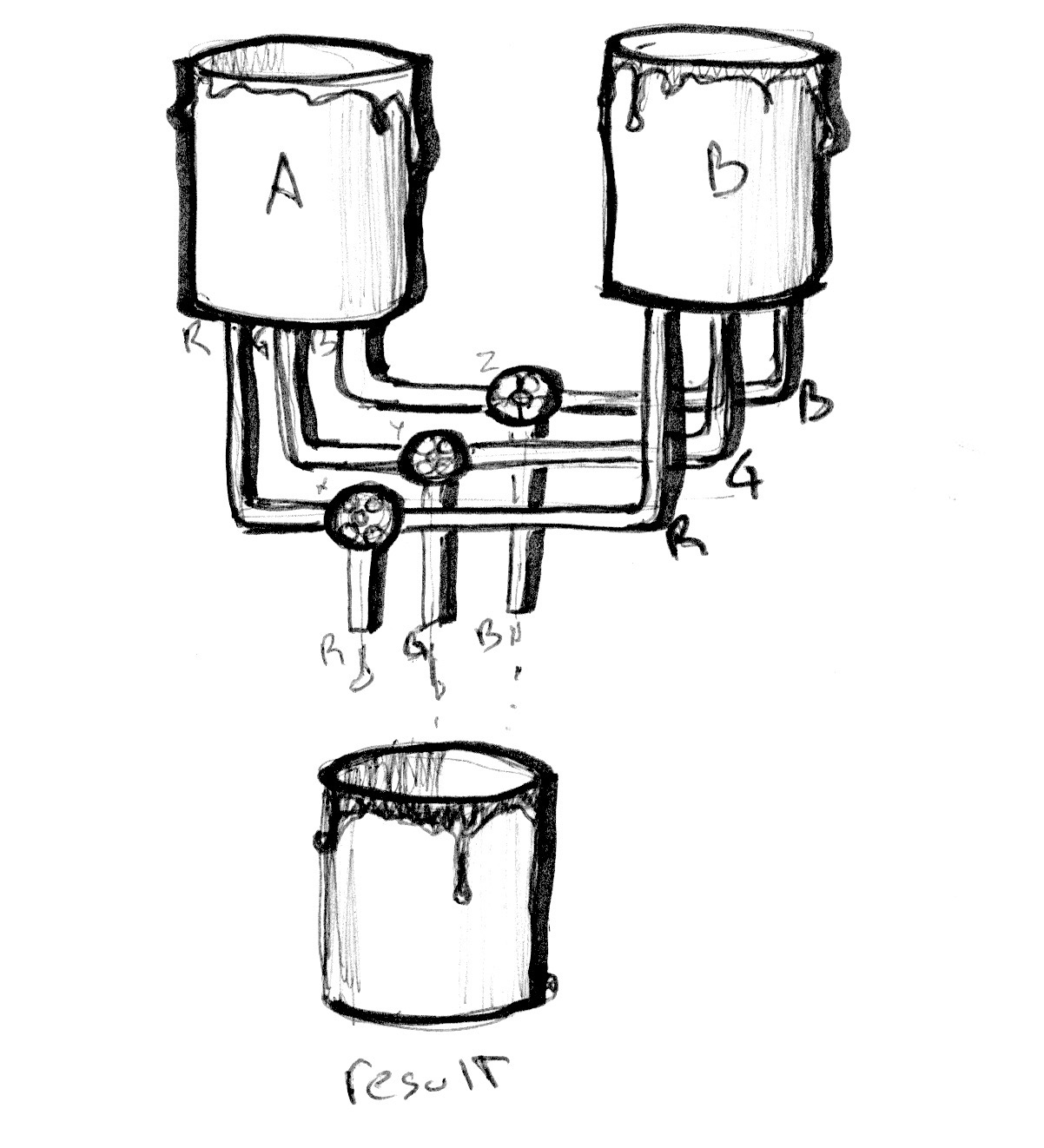
Рассмотрим следующий пример. Как и в примерах предыдущей главы, мы преобразуем значение перехода к нормализованной координате x и визуализируем его с помощью линии. Сейчас все каналы изменяются по одному и тому же закону.
Теперь раскомментируйте строку 25 и посмотрите что произойдёт. Затем попробуйте раскомментировать строки 26 и 27. Помните, что линии показывают пропорции каждого канала при смешивании цветов A и B.
Вы скорее всего узнали три функции, которые мы используем в строках 25-27. Поиграйте с ними! Исследуйте и демонстрируйте ваши находки, используя умения из предыдущей главы для создания интересных градиентов. Попробуйте выполнить следующие упражнения:
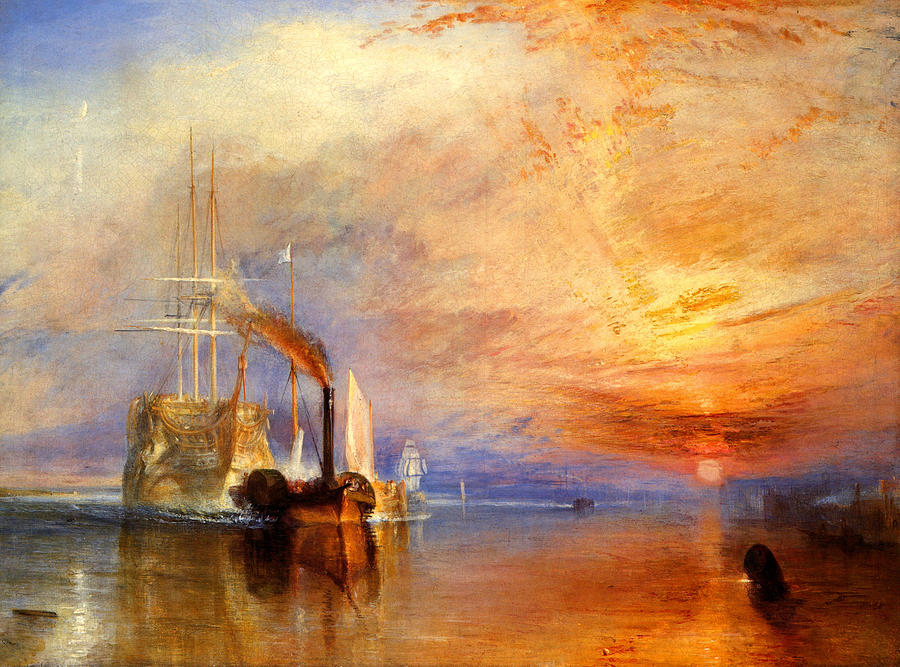
-
Создайте градиент, повторяющий закат Вильяма Тёрнера.
-
Сделайте анимацию перехода от рассвета к закату с помощью
u_time. -
Можете ли вы сделать радугу, используя изученный материал?
- Используйте функцию
step()для создания цветного флага.
HSB
Нельзя рассказать о цветах, не упомянув цветовое пространство. Как вы возможно знаете, есть множество способов задания цвета кроме красного, зелёного и синего каналов.
HSB расшифровывается как оттенок (Hue), насыщенность (Saturation) и яркость (Brightness или Value), и является более интуитивным способом представления цвета. Прочитайте код функций rgb2hsv() и hsv2rgb() в примере ниже.
Отображая координату x в оттенок, а координату y - в яркость, мы получаем красивый спектр видимых цветов. Такое пространственное распределение цветов очень удобно. Выбор цветов в пространстве HSB более интуитивен, чем RGB.
HSB в полярных координатах
Пространство HSB изначально было разработано для представления в полярных координатах (на основе угла и радиуса), вместо декартовых (x и y). Чтобы перевести нашу функцию HSB в полярные координаты, нужно вычислить угол и расстояние, используя центр области рисования и декартовы координаты пикселя. Для этого мы используем функцию вычисления расстояния length() и двухаргументный арктангенс (atan(y,x), GLSL-версия известной функции atan2(y,x)).
Тригонометрические функции от векторного аргумента вычисляются покомпонетно, даже если вы используете векторы для представления цветов. Мы начинаем использовать цвета и векторы одинаковым способом. Такая концептуальная гибкость является очень мощным инструментом.
На заметку: Возможно, вы спросите, какие ещё есть геометрически функции кроме длины (length)? Их довольно много: dot() (скалярное произведение), cross (векторное произведение), normalize() (привести вектор к единичной длине), faceforward() (вернуть вектор, указывающий в то же полупространство, что и данный), reflect() (отражение) и refract() (преломление). Так же в GLSL есть векторные функции сравнения: lessThan() (меньше), lessThanEqual() (меньше либо равно), greaterThan() (больше), greaterThanEqual() (больше либо равно), equal() (равно) и notEqual() (не равно).
Получив угол и длину, мы должны нормировать их значения в интервал от 0.0 до 1.0. В строке 27 atan(y,x) возвращает угол в радианах от минус пи до пи, поэтому сначала мы разделим его на удвоенное пи (TWO_PI, определено вначале кода), и к полученному числу от -0.5 до 0.5 прибавим 0.5, чтобы перейти в нужный интервал от 0.0 до 1.0. Максимальный радиус будет равен 0.5 (мы вычисляли расстояние от центра окна), поэтому его нужно удвоить.
Как видите, в этом разделе мы в основном играли с преобразованием значений в нужный нам промежуток от 0.0 до 1.0.
Попробуйте выполнить следующие упражнения:
-
Модифицируйте пример с полярными координатами так, чтобы цветовой круг вращался, как указатель мыши в режиме ожидания.
- Используйте функции формы совместно с функцией преобразования HSB->RGB для расширения области круга с каким-нибудь одним оттенком и урезания других оттенков.

- Присмотревшись к цветовому кругу в программах для подбора цвета (изображён ниже), можно заметить, что он пострен на основе красного, жёлтого и синего цветов. Например, напротив красного должен быть зелёный, но в нашем примере выше там находится голубой. Исправьте пример, так чтобы он выглядел в точности как изображение ниже (подсказка: используйте функции формы).

- Прочитайте книгу «Взаимодействие цветов» Джозефа Альберса и воспользуйтесь следующим примером для практики.
Заметки о функциях и аргументах
Перед тем как нырнуть в следующую главу, давайте остановимся и немного отмотаем назад. Вернитесь и взгляните на функции в предыдущих примерах. Вы заметите слово in перед типами аргументов. Это - квалификатор, и в данном случае он означает, что переменная предназначена только для чтения. В последующих примерах мы увидим так же аргументы с квалификаторами out и inout. Последний эквивалентен передаче переменной по ссылке, при которой мы можем изменить переданное значение так, что изменения становятся видны за пределами функции.
int newFunction(in vec4 aVec4, // только для чтения
out vec3 aVec3, // только на запись
inout int aInt); // чтение и записьВы не поверите, но мы уже изучили всё необходимое для создания крутой графики. В следующей главе мы научимся комбинировать все эти трюки для создания геометрических фигур с помощью смешивания пространства. Именно, смешивание пространства!