Rumore

È tempo di fare una pausa! Abbiamo giocato con le funzioni random che sembrano creare del rumore bianco di una televisione, la testa ci gira ancora solo al pensiero degli shader e i nostri occhi sono stanchi. È ora di andare a fare una passeggiata!

Sentiamo l'aria sulla nostra pelle, il sole in faccia. Il mondo è un posto così vivido e ricco: colori, texture, suoni. Mentre camminiamo, non possiamo evitare di notare la superficie delle strade, rocce, alberi e nuvole.

L'imprevedibilità di queste texture potrebbe essere intesa come "random", ma non sembrano di certo il risultato delle funzioni random che abbiamo sperimentato in precedenza. Il "mondo reale" è un posto così ricco e complesso! Come possiamo approssimare questa varietà computazionale?

Questa è stata la domanda che Ken Perlin stava cercando di risolvere nei prima anni '80 quando gli fu commissionato di generare delle texture più realistiche per il film "Tron". Il risultato delle sue ricerche fu un elegante algoritmo di rumore vincitore del premio Oscar. (Non disperatevi.)

Quanto segue non è il classico algoritmo di Perlin, ma è un buon punto di partenza per capire come generare del rumore.

In queste righe stiamo facendo qualcosa di simile a quello che abbiamo fatto nel capitolo precedente. Stiamo suddividendo un numero floating continuo (x) nel suo intero (i) e nelle componenti frazionarie (f). Usiamo floor() per ottenere i e fract() per ottenere f. Poi applichiamo rand() per la parte intera di x, che dà un valore random unico a ogni integer.

Dopo di che si osservino le due righe commentate. La prima interpola ogni valore random in modo lineare.

y = mix(rand(i), rand(i + 1.0), f);

Andate avanti e rimuovete il commento di questa linea per vedere che cosa succede. Utilizziamo la parte frazionale f per mischiare (mix()) i due valori random.

A questo punto del libro, abbiamo imparato che possiamo fare meglio d'una interpolazione lineare, giusto? Ora provate a decommentare la riga seguente, che utilizza una interpolazione smoothstep() invece di una lineare.

y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f));

Tolto il commento, si noti che la transizione tra i picchi diventa armoniosa. In alcune implementazioni del rumore, troverete che i programmatori preferiscono creare le proprie curve cubiche (come la seguente formula) invece di utilizzare la funzione smoothstep().

float u = f * f * (3.0 - 2.0 * f ); // curva cubica personalizzata
y = mix(rand(i), rand(i + 1.0), u); // e con un'interpolazione

Questo casualità armoniosa è un punto di svolta per gli ingegneri grafici o artisti perché fornisce la capacità di generare delle immagini e delle geometrie con un tocco organico. L'Algoritmo del Rumore di Perlin è stato implementato più e più volte in diversi linguaggi e spazio dimensionale per ottenere ogni tipo di uso creativo.

Ora è il vostro turno:

• Create la vostra funzione float noise(float x).

• Utilizzate la funzione di rumore per animare una forma geometrica spostandola, ruotandola o ridimensionandola.

• Fate 'ballare' diverse forme geometriche usando il rumore.

• Costruite forme "organiche" utilizzando la funzione di rumore.

• Una volta che avete la vostra "creatura", cercate di svilupparla ulteriormente assegnandogli un particolare movimento.

Rumore 2D

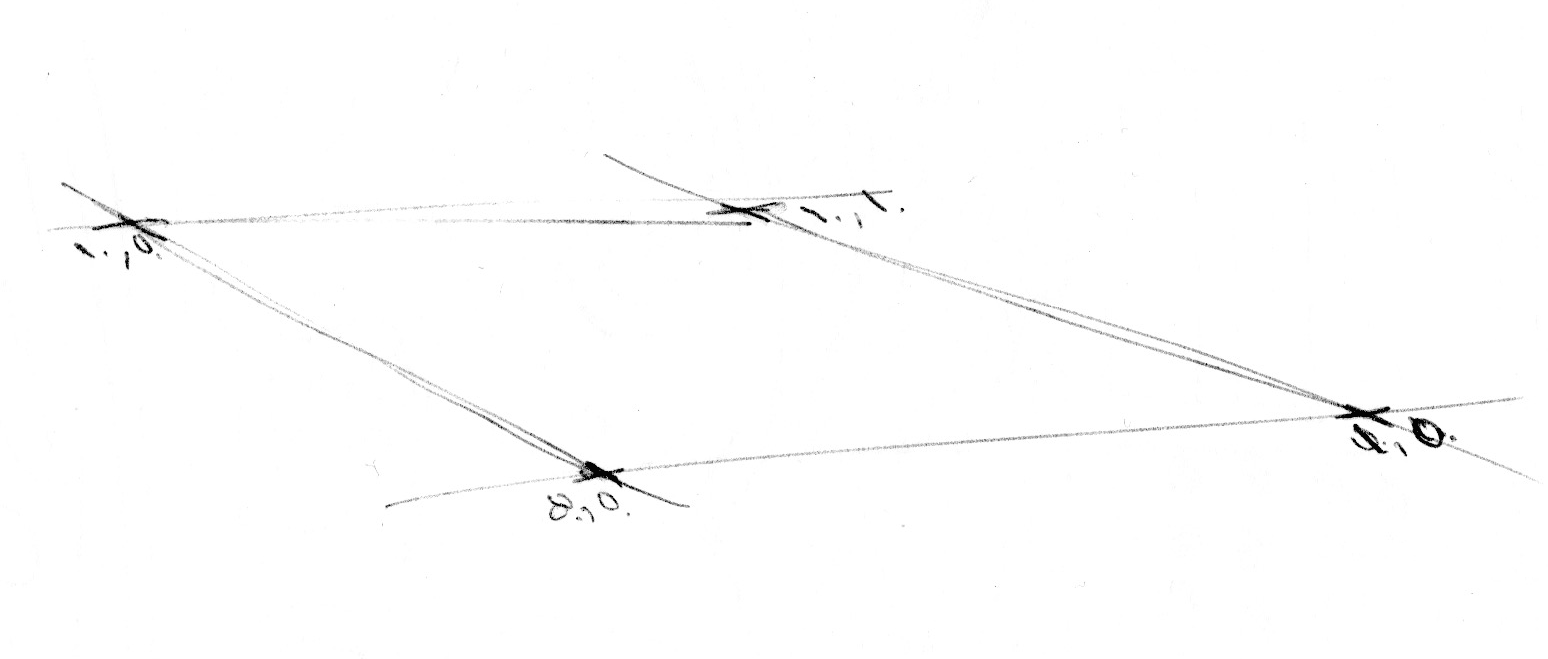
Ora che sappiamo come creare il rumore in una dimensione, è il momento di passare alla 2D. Nelle due dimensioni, invece di interpolare tra due punti di una linea (fract(x) e fract(x)+1.0), interpoleremo tra i quattro angoli di un piano quadrato (fract(st), fract(st)+vec2(1.,0.), fract(st)+vec2(0.,1.) e fract(st)+vec2(1.,1.)).

Allo stesso modo, se si vuole ottenere del rumore 3D dobbiamo interpolare tra gli otto angoli di un cubo. Questa tecnica consiste nell'interpolazione di valori random, che è il motivo per cui si chiama rumore del valore (value noise) .

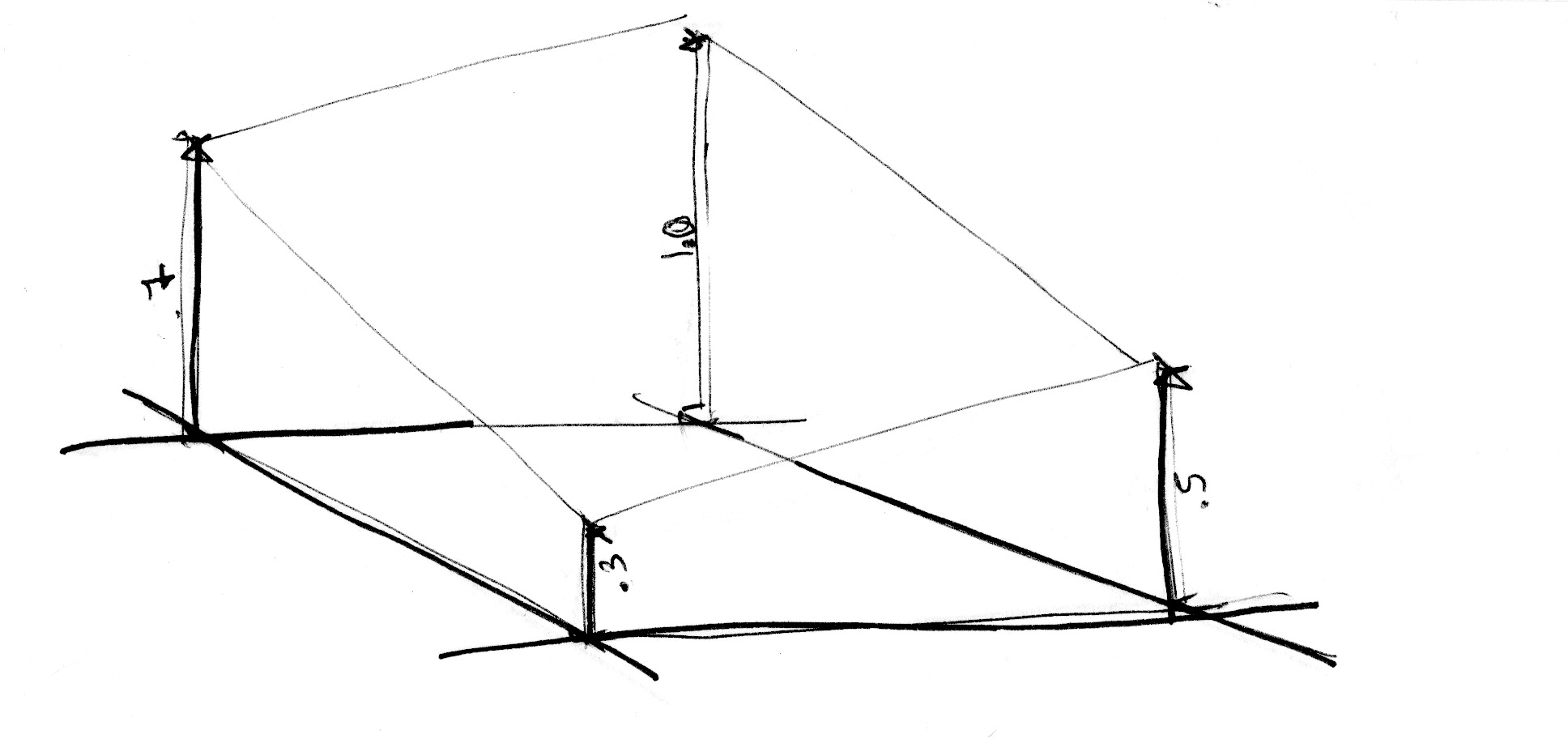
Come per l'esempio 1D, questa interpolazione non è lineare, ma cubica, e interpola senza problemi tutti i punti all'interno di una griglia quadrata.

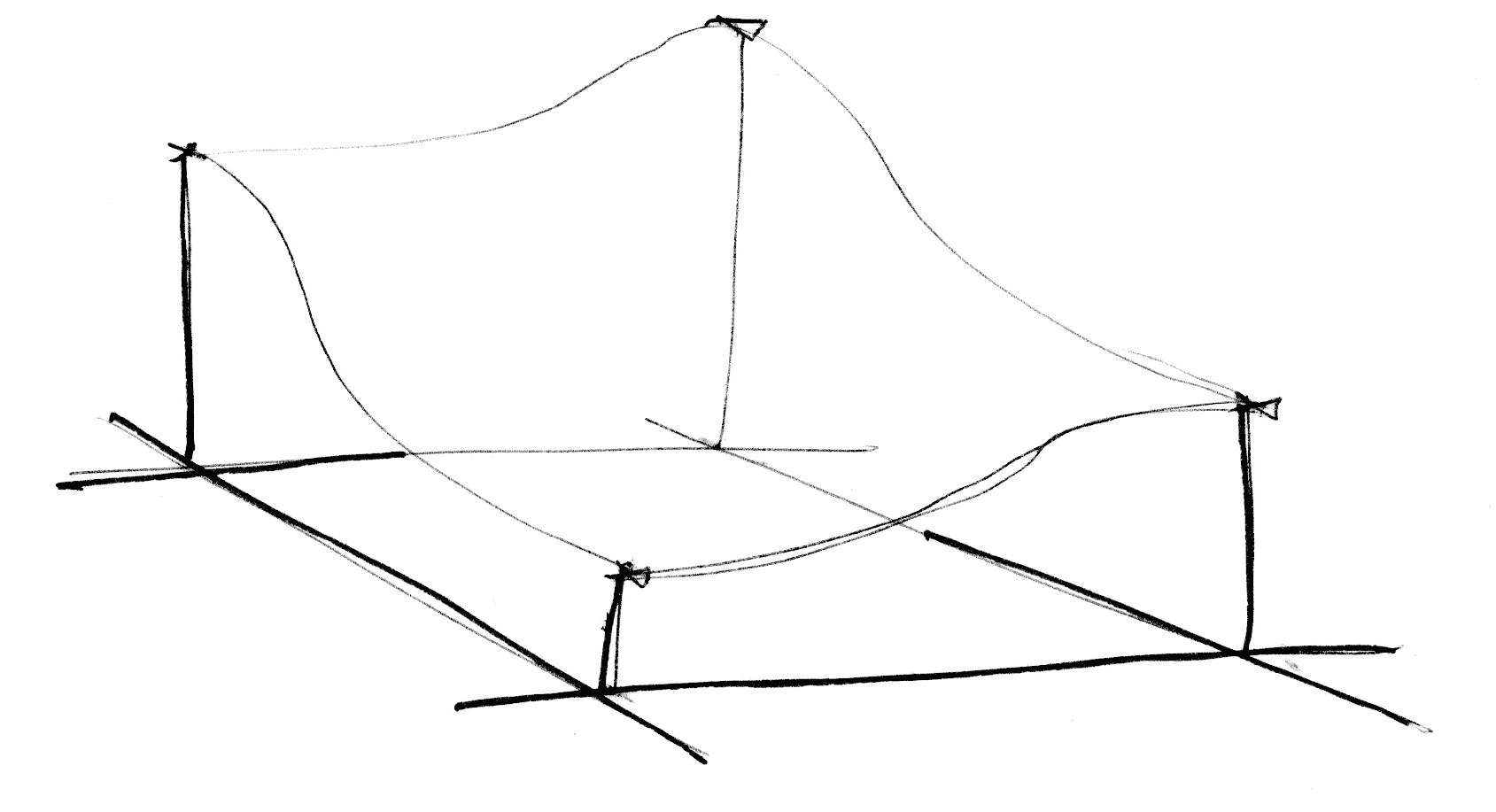
Date un'occhiata alla seguente funzione di rumore.

Iniziamo scalando lo spazio di 5 (linea 45) per vedere l'interpolazione tra i quadrati della griglia. Poi all'interno della funzione rumore suddividiamo lo spazio in celle. Memorizziamo la posizione "integer" della cella insieme alle posizioni frazionarie all'interno della cella. Usiamo la posizione dell'integer per calcolare le coordinate dei quattro angoli e ottenere un valore random per ciascuno di essi (linee 23-26). Infine, alla linea 35 interpoliamo tra i 4 valori random degli angoli utilizzando le posizioni frazionarie che abbiamo ricavato in precedenza.

Ora è il vostro turno. Provate i seguenti esercizi:

• Cambiate il moltiplicatore alla linea 45. Provate ad animarlo.

• A quale livello di zoom il rumore comincia a sembrare di nuovo random?

• A che livello di zoom il rumore è impercettibile?

• Provate a collegare questa funzione rumore alle coordinate del mouse.

• Che cosa succede se utilizziamo il gradiente del rumore come un campo di distanza? Fatene qualcosa di interessante.

• Ora che avete raggiunto un certo controllo sull'ordine e il caos, è il momento di utilizzare tale conoscenza. Effettuate una composizione di rettangoli, colori e rumore che assomiglia a un dipinto di Mark Rothko.

Usare il Rumore nella Progettazione Generativa

Gli algoritmi di rumore sono stati originariamente progettati per dare un naturale je ne sais quoi alle texture digitali. Le implementazioni 1D e 2D che abbiamo visto fino ad ora erano interpolazioni tra valori random, che è il motivo per cui sono chiamate valore di rumore, ma ci sono altri modi per ottenere il rumore...

Come avete scoperto negli esercizi precedenti, il valore del rumore tende a sembrare a dei "blocchi". Per ridurre questo effetto, nel 1985 Ken Perlin ha sviluppato un'altra implementazione dell'algoritmo denominato Rumore di Gradiente (Gradient Noise). Ken aveva capito come interpolare dei gradienti random invece che dei valori. Questi gradienti sono stati il risultato d'una funzione random 2D che restituisce le direzioni (rappresentata da un vec2) al posto di singoli valori (float). Clicca sull'immagine seguente per vedere il codice e come funziona.

Guardate questi due esempi di Inigo Quilez e prestate attenzione alle differenze tra il valore del rumore e il gradiente del rumore.

Come un pittore che capisce come i pigmenti funzionano, più sappiamo sulle varie implementazioni del rumore e meglio saremo in grado di usarle. Ad esempio, se si usa un'implementazione del rumore in due dimensioni per ruotare lo spazio in cui sono visualizzate delle linee rette, otterremo il seguente effetto visuale che sembra del legno. Anche in questo caso è possibile fare clic sull'immagine per vedere il codice.

    pos = rotate2d( noise(pos) ) * pos; // ruota lo spazio
    pattern = lines(pos,.5); // disegna delle linee

Un altro modo per ottenere dal rumore dei pattern interessanti è quello di trattarlo come un campo di distanza e applicare alcuni dei trucchi descritti nel capitolo sulle Figure.

    color += smoothstep(.15,.2,noise(st*10.)); // schizzo nero
    color -= smoothstep(.35,.4,noise(st*10.)); // buchi sugli schizzi

Un terzo modo di utilizzare la funzione di rumore è di modulare una forma. Questo richiede anche alcune delle tecniche che abbiamo imparato nel capitolo sulle figure.

Per la vostra pratica:

• Quali altri pattern generativi si possono fare? Che dire del granito? marmo? magma? acqua? Trovate tre immagini di texture di vostro interesse e come poterle realizzare algoritmicamente usando il rumore.
• Utilizzate il rumore per modulare una forma.
• Cosa succede se usate il rumore per il movimento? Tornate al capitolo sulle Matrici. Utilizzate l'esempio per traslare il "+", e applicateci alcuni movimenti random e derivati dal rumore.
• Fate un dipinto generativo alla Jackson Pollock.

Rumore Simplesso

Per Ken Perlin il successo del suo algoritmo non è stato sufficiente. Ha pensato che avrebbe potuto funzionare meglio. Al Siggraph 2001 ha presentato il "rumore simplesso", in cui ha ottenuto i seguenti miglioramenti rispetto al precedente algoritmo:

• Un algoritmo con una minore complessità computazionale e un minor numero di moltiplicazioni.
• Un rumore in grado di scalare a dimensioni superiori con meno costo computazionale.
• Un rumore senza artefatti direzionali.
• Un rumore con gradienti ben definiti e continui che possono essere calcolati abbastanza facilmente.
• Un algoritmo che è facile da implementare sull'hardware.

So cosa state pensando... "Chi è costui?" Sì, il suo lavoro è fantastico! Ma sul serio, come ha fatto a migliorare l'algoritmo? Beh, abbiamo visto come per le due dimensioni ha interpolato 4 punti (angoli di un quadrato); allo stesso modo possiamo indovinare che per tre (vedi un'implementazione qui) e quattro dimensioni abbiamo bisogno di interpolare rispettivamente 8 e 16 punti. Giusto? In altre parole per N dimensioni è necessario interpolare agevolmente dai 2 agli N punti(2^N). Ma Ken ha elegantemente notato che, anche se il quadrato è la scelta ovvia per riempire lo spazio, la figura più semplice in 2D è il triangolo equilatero. Così ha iniziato a sostituire la griglia quadrata (abbiamo appena appreso come usarla) per una griglia simplessa di triangoli equilateri.

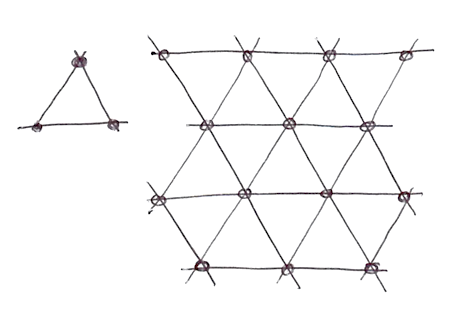
La figura simplessa per N dimensioni è una figura con N + 1 angoli. In altre parole, un angolo in meno da calcolare in 2D, 4 in meno in 3D e 11 in meno in 4D! Questo è un enorme miglioramento!

In due dimensioni l'interpolazione avviene in modo simile al rumore regolare, interpolando i valori degli angoli di una sezione. Ma in questo caso, utilizzando una griglia simplessa, abbiamo solo bisogno di interpolare la somma di 3 angoli.

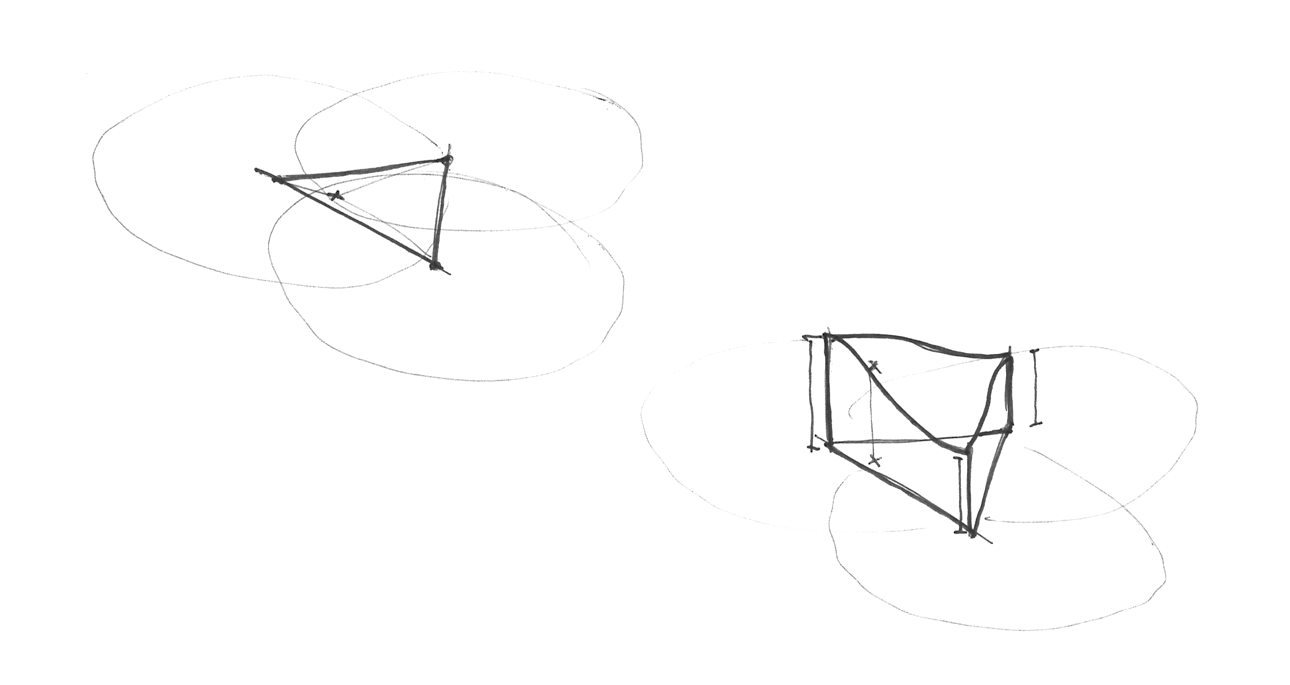
Come è fatta la griglia simplessa? Con un'altra mossa brillante ed elegante, la griglia simplessa può essere ottenuta suddividendo le celle di una regolare griglia a 4 angoli in due triangoli isosceli e poi distorcendola finché ogni triangolo sia equilatero.

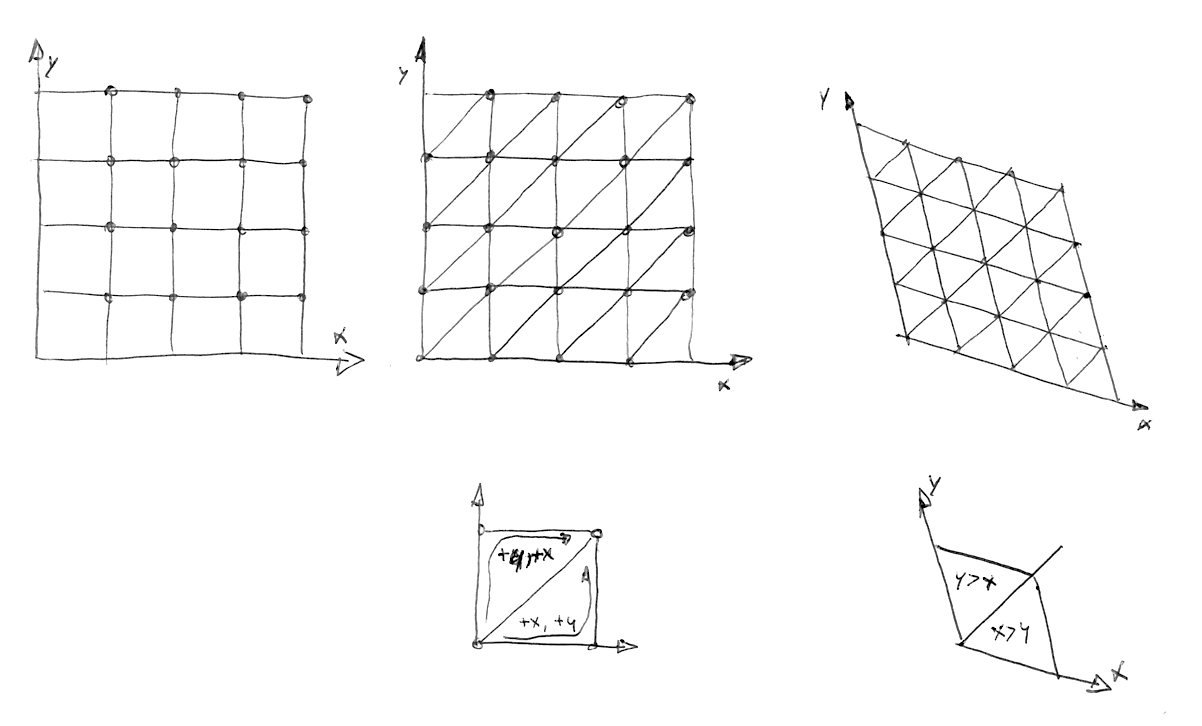
Poi, come Stefan Gustavson descrive in questo articolo: ".. cercando le parti intere delle coordinate trasformate (x,y) per il punto che vogliamo valutare, siamo in grado di determinare rapidamente quale cella di due simplessi contiene il punto. Confrontando anche le grandezze di x e y, siamo in grado di determinare se il punto è nel simplesso più alto o più basso, e percorrere i tre punti d'angolo corretti."

Nel seguente codice è possibile rimuovere il commento alla linea 44 per vedere come la griglia è distorta, e poi rimuovere il commento alla linea 47 per vedere come una griglia simplessa può essere costruita. Notate come alla linea 22 stiamo suddividendo il quadrato distorto in due triangoli equilateri semplicemente controllando se x > y (triangolo "inferiore") oppure y > x (triangolo "superiore").

Un altro miglioramento introdotto da Perlin con il Rumore Simplesso, è la sostituzione della Curva Cubica di Hermite ( f(x) = 3x^2-2x^3 , che è identica alla funzione smoothstep() ) con una Curva Quintica di Hermite ( f(x) = 6x^5-15x^4+10x^3 ). In questo modo entrambe le estremità della curva sono più "piatte" così che ogni limite si unisce con grazia con quello successivo. In altre parole si ottiene una transizione più continua tra le celle. Si può osservare ciò decommentando la seconda formula nel seguente esempio grafico (o osservando le due equazioni fianco a fianco cliccando qui).

Si noti come le estremità della curva cambino. Si può leggere di più a proposito sul sito di Ken.

Tutti questi miglioramenti si traducono in un capolavoro algoritmico noto come Rumore Simplesso. La seguente è una implementazione GLSL di questo algoritmo fatta da Ian McEwan(e presentato in questo articolo) che è troppo complicata per scopi didattici, ma sarete felici di fare un clic su di esso e vedere che è meno criptica di quanto si possa pensare.

Beh... direi che abbiamo avuto abbastanza tecnicismi, è il momento d'utilizzare queste risorse in modo creativo:

• Osservate ogni implementazione del rumore. Immaginatele come delle materie grezze, come delle rocce di marmo per uno scultore. Che cosa si può dire a proposito delle "sensazione" che ci trasmettono? Chiudete gli occhi per far scattare la vostra immaginazione, come quando si cercano delle forme in una nuvola. Cosa vedi? Cosa ricorderai? Che cosa si potrebbe creare da ogni implementazione del rumore? Seguite le vostre ispirazioni e cercate di realizzarle con il codice.

• Fate uno shader che crea l'illusione di un flusso. Come una lampada di lava, gocce d'inchiostro, dell'acqua, ecc.

• Utilizzate il rumore simplesso per aggiungere delle texture a dei lavori precedenti.

In questo capitolo abbiamo preso controllo sul caos. Non è stato un lavoro facile! Diventare un maestro del rumore richiede tempo e impegno.

Nei capitoli seguenti vedremo alcune tecniche ben note per perfezionare le proprie competenze e ottenere di più dal vostro rumore per progettare del contenuto generativo di qualità. Fino ad allora godetevi un po' di tempo all'aria aperta, contemplate la natura e i suoi pattern complicati. La capacità d'osservazione è altrettanto importante (se non di più) rispetto a quella di creare dei pattern. Andate fuori e godetevi il resto della giornata!

"Parla con l'albero, per farsi un amico." Bob Ross