Matriks 2D

Translasi

Pada bab sebelumnya kita telah mempelajari cara membuat beberapa bentuk - trik untuk memindahkan bentuk tersebut adalah dengan memindahkan sistem koordinat itu sendiri. Kita bisa mencapainya hanya dengan menambahkan vektor ke variabel st yang berisi lokasi setiap fragmen. Ini menyebabkan seluruh sistem koordinat ruang bergerak.

Ini lebih mudah dilihat daripada dijelaskan, jadi lihat sendiri:

• Hapus komentar baris 35 dari kode di bawah ini untuk melihat bagaimana ruang itu sendiri bergerak.

Sekarang coba latihan berikut:

• Menggunakan u_time bersama dengan fungsi pembentuk memindahkan tanda silang kecil dengan cara yang menarik. Telusuri kualitas gerakan tertentu yang Anda minati dan cobalah melakukan gerakan silang dengan cara yang sama. Merekam sesuatu dari "dunia nyata" terlebih dahulu mungkin berguna - bisa saja gelombang datang dan pergi, gerakan pendulum, bola yang memantul, mobil yang sedang melaju, sepeda yang berhenti.

Rotasi

Untuk memutar objek kita juga perlu memindahkan seluruh sistem ruang. Untuk itu kita akan menggunakan [matriks] (http://en.wikipedia.org/wiki/Matrix_%28mathematics%29). Matriks adalah kumpulan angka yang terorganisir dalam kolom dan baris. Vektor dikalikan dengan matriks mengikuti sekumpulan aturan yang tepat untuk mengubah nilai vektor dengan cara tertentu.

GLSL memiliki dukungan native untuk dua, tiga, dan empat dimensi matriks: [mat2](../ glossary/?search=mat2) (2x2), mat3 (3x3) dan mat4 (4x4). GLSL juga mendukung perkalian matriks (*) dan fungsi spesifik matriks (matrixCompMult()).

Berdasarkan bagaimana matriks berperilaku, dimungkinkan untuk membangun matriks untuk menghasilkan perilaku tertentu. Misalnya kita dapat menggunakan matriks untuk menerjemahkan vektor:

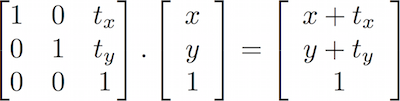
Menariknya, kita bisa menggunakan matriks untuk memutar sistem koordinat:

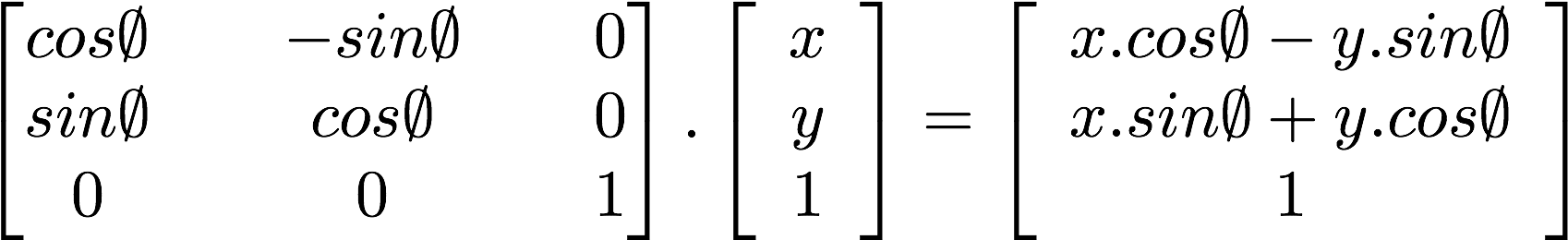
Perhatikan kode berikut untuk fungsi yang menyusun matriks rotasi 2D. Fungsi ini mengikuti [rumus] (http://en.wikipedia.org/wiki/Rotation_matrix) di atas untuk vektor dua dimensi untuk memutar koordinat di sekitar titik vec2(0.0).

mat2 rotate2d(float _angle){
    return mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle));
}

Menurut cara kita menggambar bentuk, ini bukanlah yang kita inginkan. Bentuk silang kami digambar di tengah kanvas yang sesuai dengan posisi vec2(0,5). Jadi, sebelum kita memutar ruang kita perlu memindahkan bentuk dari center ke koordinat vec2(0.0), putar spasi, lalu pindahkan kembali ke tempat semula.

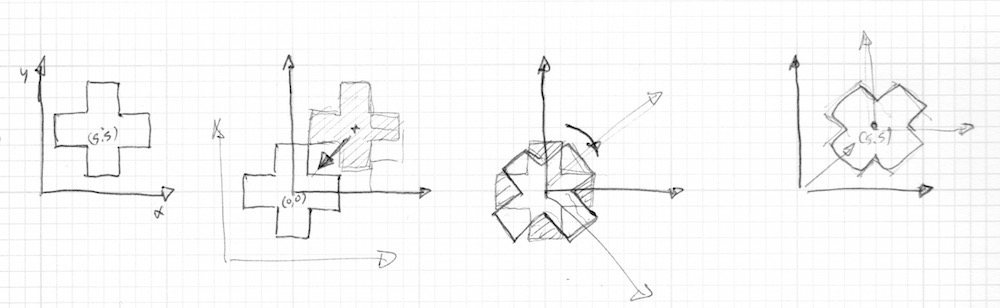
Itu terlihat seperti kode berikut:

Coba latihan berikut:

• Hapus tanda komentar baris 45 kode diatas dan perhatikan apa yang terjadi.

• Komentari terjemahan sebelum dan sesudah rotasi, pada baris 37 dan 39, dan amati konsekuensinya.

• Gunakan rotasi untuk meningkatkan animasi yang Anda simulasi dalam latihan penerjemahan.

Skala

Kami telah melihat bagaimana matriks digunakan untuk menerjemahkan dan memutar objek di ruang angkasa. (Atau lebih tepatnya untuk mentransformasikan sistem koordinat untuk memutar dan memindahkan objek.) Jika Anda telah menggunakan perangkat lunak pemodelan 3D atau fungsi matriks push dan pop dalam Pemrosesan, Anda akan tahu bahwa matriks juga dapat digunakan untuk menskalakan ukuran sebuah obyek.

Mengikuti rumus sebelumnya, kita bisa mengetahui cara membuat matriks penskalaan 2D:

mat2 scale(vec2 _scale){
    return mat2(_scale.x,0.0,
                0.0,_scale.y);
}

Cobalah latihan berikut untuk memahami lebih dalam cara kerjanya.

• Hapus komentar baris 42 kode di atas untuk melihat koordinat spasi sedang diskalakan.

• Lihat apa yang terjadi jika Anda mengomentari terjemahan sebelum dan sesudah penskalaan pada baris 37 dan 39.

• Coba gabungkan matriks rotasi bersama dengan matriks skala. Ketahuilah bahwa urutan itu penting. Kalikan dengan matriks terlebih dahulu lalu kalikan vektornya.

• Sekarang setelah Anda tahu cara menggambar berbagai bentuk, dan memindahkan, memutar, dan menskalakannya, sekarang saatnya membuat komposisi yang bagus. Mendesain dan membuat UI atau HUD palsu (tampilan kepala ke atas). Gunakan contoh ShaderToy berikut oleh Ndel untuk inspirasi dan referensi.

Kegunaan lain untuk matriks: Warna YUV

YUV adalah ruang warna yang digunakan untuk pengkodean analog foto dan video yang memperhitungkan jangkauan persepsi manusia untuk mengurangi bandwidth komponen chrominance.

Kode berikut adalah kesempatan menarik untuk menggunakan operasi matriks di GLSL untuk mengubah warna dari satu mode ke mode lainnya.

Seperti yang Anda lihat, kami memperlakukan warna sebagai vektor dengan mengalikannya dengan matriks. Dengan cara itu kita "memindahkan" nilai-nilai itu.

Dalam bab ini kita telah mempelajari bagaimana menggunakan transformasi matriks untuk memindahkan, memutar dan menskalakan vektor. Transformasi ini akan sangat penting untuk membuat komposisi dari bentuk yang telah kita pelajari di bab sebelumnya. Di bab selanjutnya kita akan menerapkan semua yang telah kita pelajari untuk membuat pola prosedural yang indah. Anda akan menemukan bahwa pengulangan dan variasi pengkodean bisa menjadi praktik yang menarik.