2D-Matrizen

Verschieben

Im letzten Kapitel haben wir gesehen, wie man unterschiedliche Formen zeichnet. Der Trick, um diese Formen auf der Zeichenfläche beliebig zu positionieren, besteht nun darin, das Koordinatensystem „unterhalb“ dieser Formen zu verschieben. Wir erreichen dies, indem wir einfach einen Vektor zu der st-Variable addieren, die die Lage des jeweiligen Objekts beim Zeichnen bestimmt. Dadurch verschiebt sich das gesamte Koordinatensystem.

Es ist vermutlich einfacher, das Verfahren in der Praxis nachzuvollziehen, als es in der Theorie zu studieren. Schau einfach selbst:

• Entferne die Kommentarzeichen in der Programmzeile 35, und Du wirst sehen, wie sich das Zeichenobjekt gemeinsam mit dem darunterliegenden Koordinatenraum bewegt.

Jetzt versuche Dich an der folgenden Aufgabe:

• Nutze u_time in Verbindung mit einer formgebenden Funktion, um das kleine Kreuz auf interessante Weise über die Zeichenfläche zu bewegen. Das Vorbild dafür kann durchaus aus der realen Welt stammen, beispielsweise eine Wellenbewegung, das Schwingen eines Pendels, ein springender Ball, ein beschleunigendes Auto oder ein stoppendes Fahrrad.

Rotationen

Um Objekte rotieren zu lassen, müssen wir ebenfalls nur das zugrundeliegende Koordinatensystem transformieren. Wir verwenden dafür eine Rotationsmatrix. Eine Matrix ist eine geordnete Anordnung von Zahlen in Form von Zeilen und Spalten. Vektoren werden mit Matrizen nach einem festen vorgegebenen Verfahren multipliziert, um den Vektor auf eine bestimmte Art und Weise zu verändern.

GLSL verfügt über eingebaute Unterstützung für zwei-, drei- und vierdimensionale Matrizen: mat2 (2x2), mat3 (3x3) und mat4 (4x4). Außerdem unterstützt GLSL die Matrizenmultiplikation (*) mit einem Vektor sowie die Multiplikation zweier Matrizen mit der speziellen Funktion (matrixCompMult()).

Darauf basierend, wie Matrizen funktionieren, kann man Matrizen mit einem bestimmten „Verhalten“ konstruieren. Beispielsweise können wir eine Matrix zum Verschieben eines Vektors nutzen:

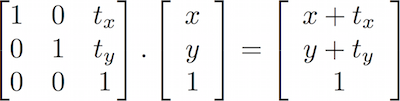
Noch interessanter wird es, wenn wir eine Matrix zur Drehung des Koordinatensystems verwenden:

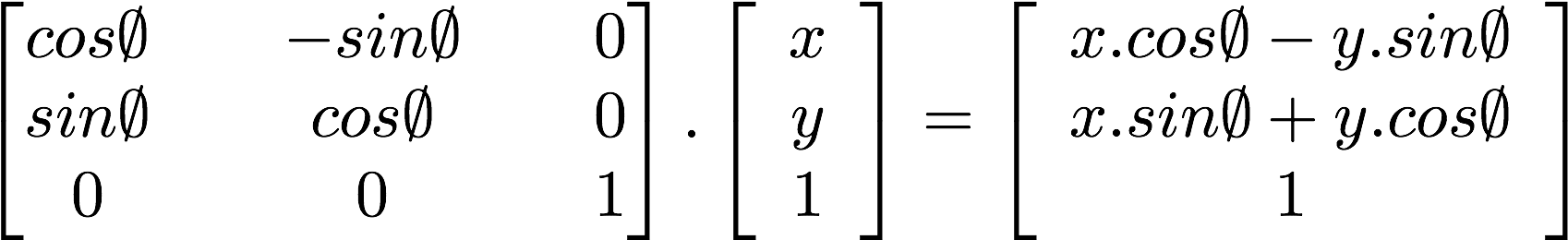
Schau Dir den folgenden Programmcode an, der die benötigte Matrix für eine Rotation des Koordinatensystems um einen vorgegebenen Winkel produziert. Diese Funktion folgt der obigen Formel für zweidimensionale Vektoren, um die Koordinaten um einen vec2(0.0)-Punkt rotieren zu lassen.

mat2 rotate2d(float _angle){
    return mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle));
}

In Bezug auf die Art und Weise, wie wir Formen bislang gezeichnet haben, ist das noch nicht ganz das, was wir benötigen. Unser Kreuz wird auf der Mitte der Zeichenfläche generiert, ausgehend vom Punkt vec2(0.5). Vor der Rotation müssen wir die Form deshalb von der Mitte des Koordinatensystem zum vec2(0.0) verschieben, anschließend die Drehung ausführen und das Objekt dann wieder an seinen ursprünglichen Platz bringen.

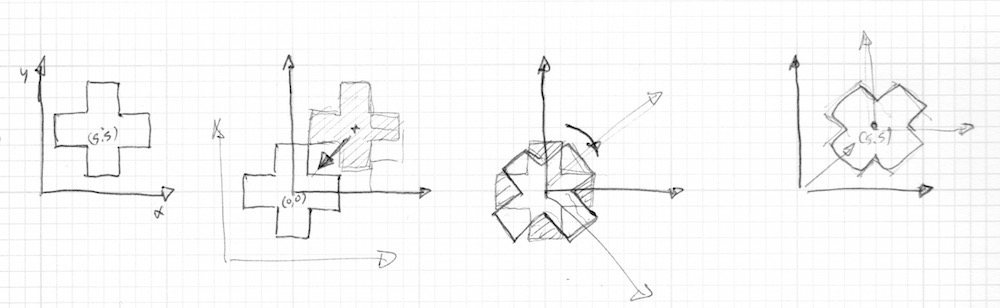
In Programmcode „gegossen“, sieht das dann wie folgt aus:

Probiere die folgenden Übungen aus:

• Entferne die Kommentarzeichnen aus der Programmzeile 45 und beobachte, was dann passiert.

• Kommentiere das Verschieben vor und nach der Rotation in den Zeilen 37 und 39 aus und beobachte die Konsequenzen.

• Nutze Rotationen, um die Animation zu verbessern, die Du beim Beispiel zum Verschieben erstellt hast.

Skalieren

Wir haben gesehen, wie man die Verschiebung und die Rotation von Objekten realisiert, indem man mit Matrizen auf den Koordinatenraum einwirkt. Falls Du bereits mit 3D-Modellierungssoftware oder den Matrizenfunktionen in Procesing gearbeitet hast, weißt Du wahrscheinlich, dass man Matrizen auch für die Skalierung von Objekten verwenden kann.

Indem wir uns an der obigen Formel orientieren, können wir eine 2D-Saklierungsmatrix für das gewünschte Vergrößern oder Verkleinern erstellen:

mat2 scale(vec2 _scale){
    return mat2(_scale.x,0.0,
                0.0,_scale.y);
}

Probiere die folgenden Übungen aus, um noch besser zu verstehen, wie das Ganze funktioniert.

• Entferne die Kommentare in der Programmzeile 42, um zu sehen, wie der Koordinatenraum skaliert wird.

• Schau Dir an, was geschieht, wenn Du die Verschiebung vor und nach der Skalierung in den Programmzeilen 37 und 39 entfernst.

• Probiere eine Rotationsmatrix in Verbindung mit einer Skalierungsmatrix aus. Sei Dir bewusst, dass die Reihenfolge der Matrixoperationen dabei eine entscheidende Rolle spielt.

• Jetzt, wo Du weißt, wie man unterschiedliche Formen malt, verschiebt, rotiert und skaliert, ist es an der Zeit, eine etwas komplexere Komposition zu erstellen. Designe und entwickle die Simulation einer futuristischen Benutzeroberfläche bzw. eines Head-up-Displays. Nutze das folgende Beispiel aus den Shadertoys von Ndel als Inspirationsquelle und als Referenz.

Ein anderes Einsatzgebiet für Matrizen: YUV-Farben

YUV ist ein Farbmodell, das für die analoge Kodierung von Fotos und Videos verwendet wird. Das Modell berücksichtigt die Grenzen der menschlichen Farbwahrnehmung und nutzt dies für die Beschränkung der Bandbreite (der benötigten Bits) bei der Kodierung der Farbigkeit (Chrominanz).

Der folgende Programmcode zeigt eine interessante Einsatzmöglichkeit für den Einsatz von Matrizenfunktionen zur Konvertierung von Farben zwischen zwei Farbräumen bzw. Farbsystemen.

Wie Du siehst, behandeln wir Farben hier als Vektoren, indem wir sie mit Matrizen multiplizieren. Auf diese Weise können wir die Farben über ihre Farbwerte hin und her bewegen.

In diesem Kapitel haben wir gelernt, wie man Matrixtransformationen für das Verschieben, Rotieren und Skalieren von Vektoren nutzt. Für die Erstellung von Kompositionen aus mehreren grafischen Formen und Objekten sind diese Transformationen essenziell. Im nächsten Kapitel werden wir all das Erlernte anwenden, um bezaubernde prozedurale Muster zu erstellen. Du wirst sehen, dass die Wiederholung und Variation von Programmcode höchst interessante Resultate liefern kann.