Macierze 2D

Translacja

W poprzednim rozdziale dowiedzieliśmy się, jak tworzyć różne kształty. Przesuwanie tych kształtów polega na przesuwaniu samego układu współrzędnych. Możemy to osiągnąć poprzez proste dodanie wektora do zmiennej st, zawierającej położenie każdego fragmentu. Powoduje to przesunięcie całego układu współrzędnych.

Łatwiej jest to zobaczyć niż wytłumaczyć, zatem:

*Odkomentuj linijkę 35 poniższego kodu, by zobaczyć jak przestrzeń się przesuwa.

Spróbuj teraz wykonać następujące ćwiczenie:

• Używając u_time wraz z shaping functions poruszaj małym krzyżem w ciekawy sposób. Poszukaj interesującego cię ruchu i spróbuj sprawić, by krzyż poruszał się w ten sam sposób. Przydatne może być nagranie najpierw czegoś z "prawdziwego świata" - może to być przypływ i odpływ fal, ruch wahadła, odbijająca się piłka, przyspieszający samochód, zatrzymujący się rower.

Rotacja

Aby obracać obiekty również musimy poruszać całym układem przestrzennym. Do tego celu będziemy używać macierzy. Macierz to uporządkowany zbiór liczb w kolumnach i wierszach. Wektory są mnożone przez macierze według ściśle określonych reguł w celu zmodyfikowania wartości wektora w określony sposób.

GLSL posiada natywne wsparcie dla dwu, trzy i czterowymiarowych macierzy: mat2 (2x2), mat3 (3x3) i mat4 (4x4). GLSL obsługuje również mnożenie macierzy (*) oraz specyficzną dla macierzy funkcję matrixCompMult().

Na podstawie tego, jak zachowują się macierze, możliwe jest skonstruowanie macierzy w celu wytworzenia określonych zachowań. Na przykład możemy użyć macierzy do translacji wektora:

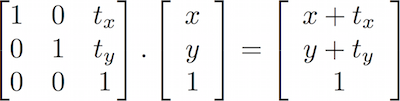
Co ciekawsze, możemy użyć macierzy do obrócenia całego układu współrzędnych

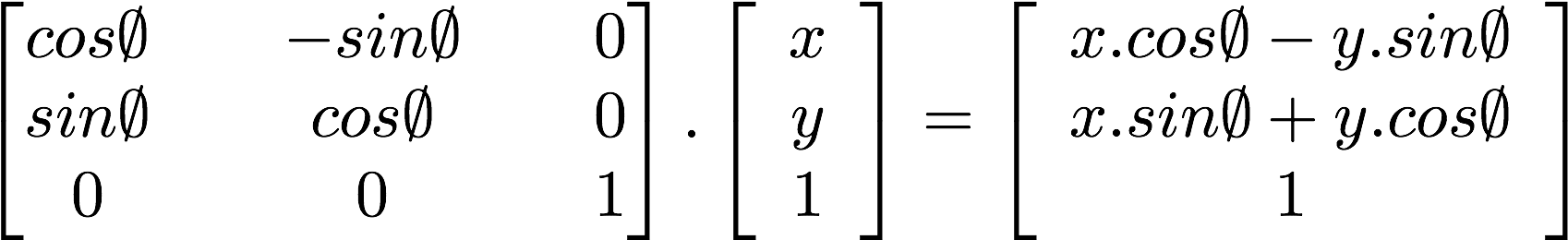
Spójrz na poniższy kod funkcji, która konstruuje dwuwymiarową macierz rotacji. Funkcja ta oparta jest na wzorze dla dwuwymiarowych wektorów, aby obrócić współrzędne wokół punktu vec2(0,0).

mat2 rotate2d(float _angle){
    return mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle));
}

Zgodnie ze sposobem, w jaki rysowaliśmy kształty, nie jest to dokładnie to, czego chcemy. Nasz krzyż jest rysowany w centrum płótna, co odpowiada pozycji vec2(0.5). Tak więc, zanim obrócimy przestrzeń musimy przenieść ten krzyż z centrum na współrzędną vec2(0.0), obrócić przestrzeń, a następnie ostatecznie przenieść go z powrotem na pierwotne miejsce.

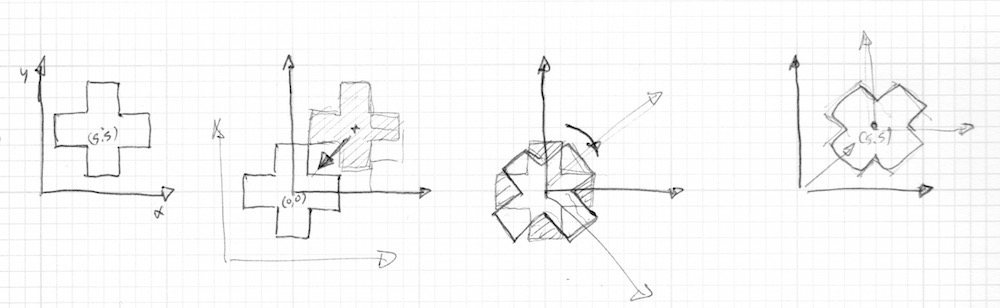
Co odpowiada ponizszemu kodowi:

Spróbuj wykonać następujące ćwiczenia:

• Odkomentuj linię 45 powyższego kodu i zwróć uwagę na to, co się stanie.

• Zakomentuj translacje przed i po rotacji, w liniach 37 i 39, i zaobserwuj konsekwencje.

• Użyj rotacji, aby poprawić ruch, który zasymulowałeś w ćwiczeniu z podrozdziału "Translcja".

Skalowanie

Widzieliśmy już, jak macierze służą do translacji i rotacji obiektów w przestrzeni. (A dokładniej do przekształcania układu współrzędnych w celu obracania i przesuwania obiektów). Jeśli używałeś programów do modelowania 3D albo funkcji macierzowych push i pop w Processing, to pewnie wiesz, że macierze mogą być również używane do skalowania rozmiaru obiektu.

Na podstawie powyższego wzoru, możemy stworzyć 2D macierz skalowania w GLSL:

mat2 scale(vec2 _scale){
    return mat2(_scale.x,0.0,
                0.0,_scale.y);
}

Spróbuj następujących ćwiczeń, aby głębiej zrozumieć, jak to działa.

• Odkomentuj linię 42 powyższego kodu, aby zobaczyć skalowanie współrzędnych przestrzeni.

• Zobacz, co się stanie, gdy zakomentujesz translacje przed i po skalowaniu w liniach 37 i 39.

• Spróbuj połączyć macierz rotacji wraz z macierzą skalowania. Bądź świadomy, że kolejność ma znaczenie. Najpierw pomnóż przez macierz, a potem pomnóż wektory.

• Teraz, gdy wiesz już, jak rysować różne kształty oraz przesuwać, obracać i skalować je, czas na stworzenie ładnej kompozycji. Zaprojektuj i skonstruuj UI lub HUD (ang. "heads up display"). Użyj następującego przykładu ShaderToy autorstwa Ndel jako inspiracji.

Inne zastosowania macierzy: Kolor YUV

YUV to przestrzeń barw stosowana do analogowego kodowania zdjęć i filmów, która uwzględnia ludzką percepcję w celu zmniejszenia redundantnych informacji zawartych w reprezentacji RGB.

Poniższy kod jest ciekawą okazją do wykorzystania operacji macierzowych w GLSL do transformacji kolorów z jednej przestrzeni do drugiej.

Jak widać traktujemy kolory jak wektory, które można mnożyć przez macierze. W ten sposób mapujemy wartości.

W tym rozdziale dowiedzieliśmy się, jak używać przekształceń macierzowych do przesuwania, obracania i skalowania wektorów. Przekształcenia te będą niezbędne do tworzenia kompozycji z kształtów, które poznaliśmy w poprzednim rozdziale. W następnym rozdziale zastosujemy wszystko, czego dotychczas się nauczyliśmy, do tworzenia pięknych proceduralnych wzorów. Zobaczysz, że programowanie powtórzeń i wariacji może być bardzo ekscytujące.