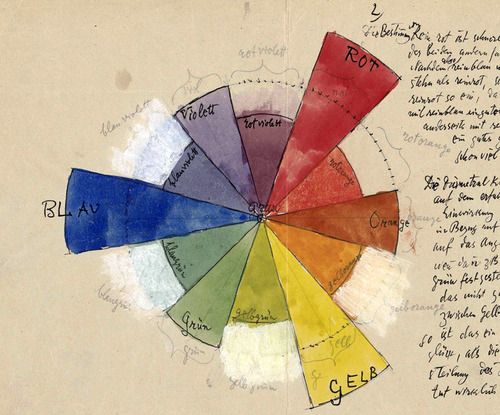
Кольори

Раніше у нас не було нагоди поговорити про векторні типи GLSL. Перш ніж рушити далі, важливо дізнатися про них більше. А тема кольорів якраз дуже підходить для цього і буде чудовим шляхом для такого знайомства.

Якщо ви знайомі з парадигмами об'єктноорієнтованого програмування, то, мабуть, помітили, що ми зверталися до даних у векторах, як до будь-якої звичайної C-подібної структури.

vec3 red = vec3(1.0, 0.0, 0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

Визначення кольору за допомогою нотації x, y і z може заплутати й ввести в оману, чи не так? Ось чому існують й інші способи доступу до цієї самої інформації, але під іншими іменами. Значення .x, .y і .z так само можна отримати через .r, .g і .b, а також через .s, .t і .p. (.s, .t і .p зазвичай використовуються для роботи з просторовими координатами текстури, які ми побачимо в наступному розділі.) Крім того, ви також можете отримати доступ до елементів вектора через позицію індексу: [0], [1] і [2].

Наступні рядки показують всі способи доступу до тих самих даних:

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

Всі ці різні способи посилання на змінні всередині вектора — лише додаткові номенклатури — розроблені позначення, щоб допомогти вам написати чіткіший код. Ця гнучкість, вбудована в мову шейдерів, дає вам можливість почати думати про просторові координати та значення кольорів як про взаємозамінні сутності.

Ще одна чудова особливість векторних типів у GLSL полягає в тому, що їх властивості можна комбінувати в будь-якому довільному порядку, що спрощує приведення та змішування значень. Ця здатність називається змішуванням.

vec3 yellow, magenta, green;

// Створення жовтого кольору
yellow.rg = vec2(1.0);  // Присвоєння 1.0 червоному та зеленому каналам
yellow[2] = 0.0;        // Присвоєння 0.0 синьому каналу

// Створення пурпурового кольору
magenta = yellow.rbg;   // Присвоєння каналів зі зміною місць зеленого і синього. rbg замість rgb

// Створення зеленого кольору
green.rgb = yellow.bgb; // Присвоєння значення синього каналу зі змінної "yellow" червоному і синьому каналам змінної "red"

Змішування кольорів

Тепер, коли ви знаєте, як визначаються кольори, настав час об'єднати ці нові знання з попередніми. У GLSL є дуже корисна функція mix(), яка дозволяє змішувати два значення у відсотках. Чи можете ви здогадатися, який саме там діапазон? Так, звісно це значення від 0.0 до 1.0! Ідеально підійде для вас, особливо після довгих годин відпрацювання рухів карате з парканом – настав час скористатися ними!

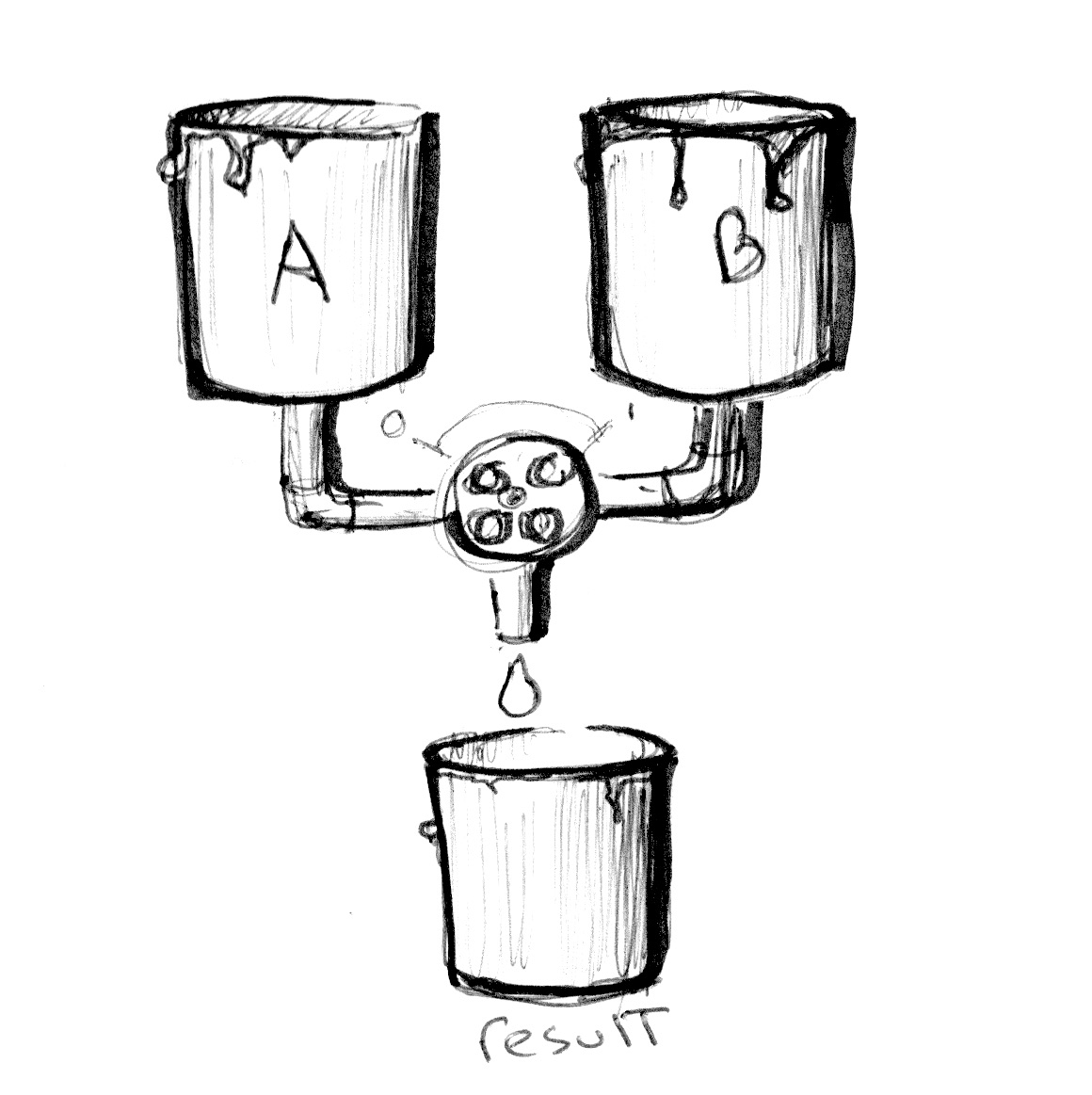
Перевірте наступний код у рядку 18 і подивіться, як ми використовуємо абсолютні значення синусу на основі часу, щоб змішати значення кольорів у змінних colorA та colorB.

Покажіть свої навички:

• Зробіть експресивний перехід між кольорами. Подумайте про якусь емоцію. Який колір здається найбільш характерним для неї? Як він з'являється? Як зникає? Подумайте про іншу емоцію та відповідний їй колір. Змініть початковий і кінцевий кольори у коді вище, відповідно цим емоціям. Потім анімуйте перехід за допомогою формотворчих функцій. Robert Penner розробив серію популярних функцій для комп'ютерної анімації, відомих як функції пом'якшення. Ви можете використати цей приклад для дослідження та натхнення, але найкращий результат ви здобудете, налаштувавши свої власні переходи.

Гра з градієнтами

Функція mix() може запропонувати більше. Замість одного float значення ми можемо передати компонентний тип змінної, однаковий для перших двох аргументів, у нашому випадку це vec3. Таким чином ми отримуємо контроль над відсотками змішування кожного окремого каналу кольорів: r, g і b.

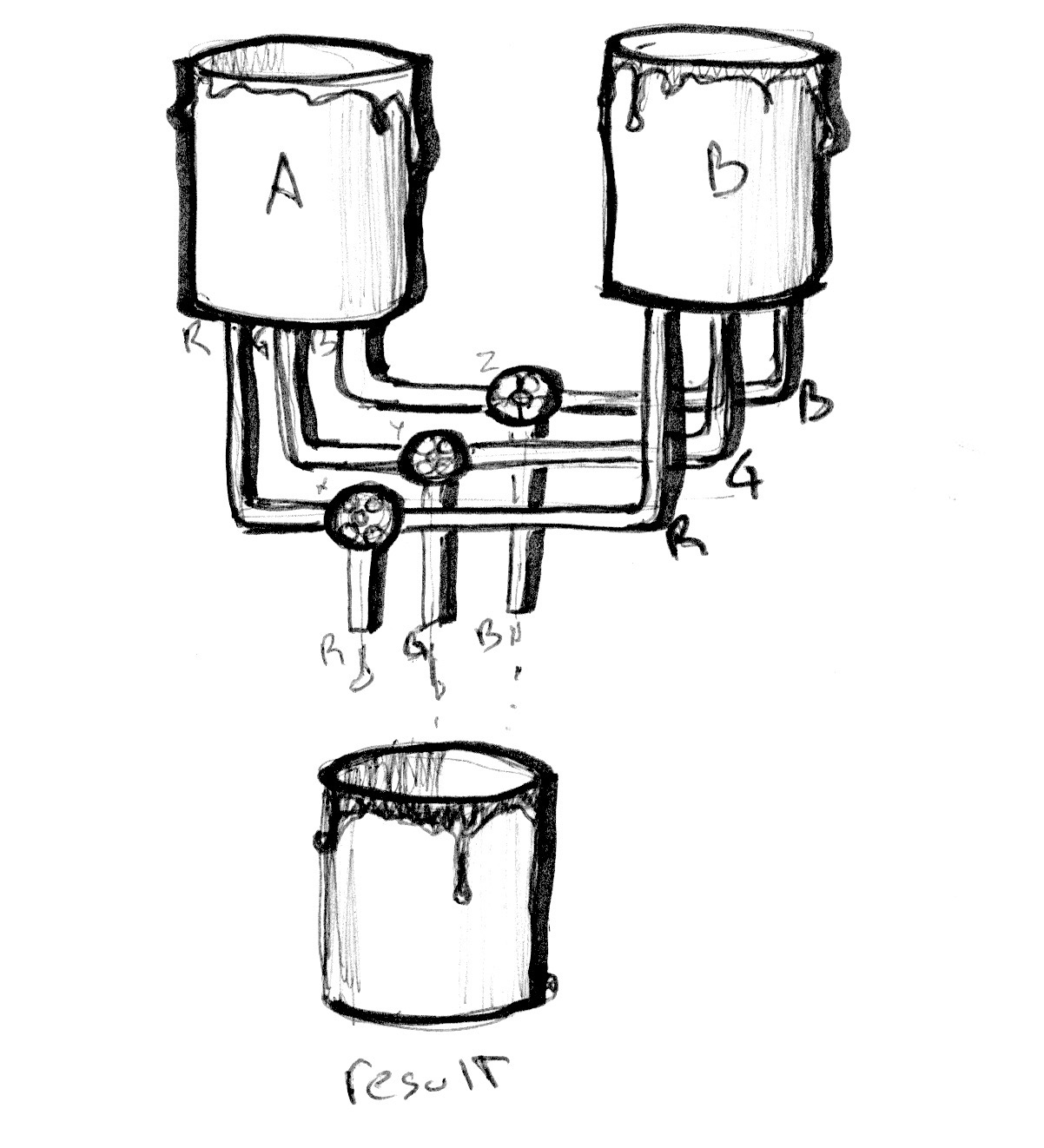
Розгляньте наступний приклад. Як і в прикладах попереднього розділу, ми створюємо нормалізовані координати та використовуємо x для візуалізації лінії. Зараз усі канали змінюються по спільному правилу.

Тепер розкоментуйте рядок 25 і подивіться, що станеться. Потім спробуйте розкоментувати рядки 26 і 27. Пам’ятайте, що лінії візуалізують вагу змішування кожного каналу змінних colorA та colorB.

Ви, напевно, впізнали три функції, які ми використовуємо в рядках 25-27. Пограйте з ними! Настав час дослідити та продемонструвати свої навички з попереднього розділу та створити цікаві градієнти. Спробуйте наступні вправи:

• Створіть градієнт, що нагадує захід сонця Вільяма Тернера

• Анімуйте перехід між сходом і заходом сонця за допомогою u_time.

• Чи можете ви зробити веселку, використовуючи отримані до цього часу знання?

• Використайте функцію step(), щоб створити кольоровий прапор.

HSB

Ми не можемо говорити про колір, не згадавши про колірний простір. Як ви, напевно, знаєте, існують різні способи організації кольорів, окрім червоного, зеленого та синього каналів.

HSB означає відтінок (Hue), насиченість (Saturation) і яскравість (Brightness або Value) і є більш інтуїтивно зрозумілою організацією кольорів. Прочитайте код функцій rgb2hsv() і hsv2rgb() у наступному прикладі.

Зіставляючи x-координату на відтінок та y-координату на яскравість, ми отримуємо гарний спектр видимих кольорів. Такий просторовий розподіл кольору може бути дуже зручним. Вибір кольору з простору HSB більш інтуїтивний, ніж з RGB.

HSB в полярних координатах

HSB початково розроблений для представлення в полярних координатах (на основі кута та радіуса) замість декартових координат (на основі x і y). Щоб зіставити нашу функцію HSB з полярними координатами, нам потрібно отримати кут і відстань від центру полотна до піксельної координати. Для цього ми використаємо функцію розрахунку відстані — length() і арктангенс — atan(y, x) (GLSL-версія загальновживаної функції atan2(y, x)).

Під час використання векторних і тригонометричних функцій типи vec2, vec3 і vec4 розглядаються як вектори, навіть якщо вони представляють кольори. Ми почнемо обробляти кольори та вектори однаковим чином. Згодом ви побачите, що ця концептуальна гнучкість дуже розширює ваші можливості.

Примітка: Якщо вам цікаво, то окрім length існують й інші геометричні функції, наприклад: distance(), dot(), cross(), normalize(), faceforward(), reflect() та refract(). Також GLSL має спеціальні векторні функції порівняння, такі як: lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() та notEqual().

Отримавши кут і довжину, нам потрібно "нормалізувати" їх значення у діапазоні від 0.0 до 1.0. У рядку 27 atan(y, x) поверне кут у радіанах між -PI та PI (від -3.14 до 3.14). Тому нам потрібно розділити це число на подвійне PI, яке записане у макрос TWO_PI, що визначений у верхній частині коду. Це дозволить нам отримати значення від -0.5 до 0.5, які шляхом простого додавання до них значення 0.5 ми змінимо на бажаний діапазон від 0.0 до 1.0. Радіус поверне максимум 0.5 (оскільки ми обчислюємо відстань від центру вікна перегляду), тому нам потрібно подвоїти цей діапазон (множенням на два), щоб отримати максимум 1.0.

Як бачите, наша гра полягає в перетворенні та масштабуванні значень, які нам потрібні у діапазоні від 0.0 до 1.0.

Спробуйте наступні вправи:

• Змініть приклад з полярними координатами, щоб отримати колірне коло, що обертається, як невелике коло біля екранного курсора в режимі очікування.

• Використайте функцію формування разом із функцією перетворення кольору з HSB у RGB, щоб розширити область кола з певним відтінком та звузити решту.

• Якщо ви уважно придивитесь на колірне коло у програмних палітрах кольорів (див. зображення нижче), ви побачите, що вони використовують інший спектр відповідно до колірного простору RYB. Наприклад, колір, напроти червоного повинен бути зеленим, але в нашому прикладі вище це блакитний. Спробуйте змінити код прикладу, щоб отримати таке саме коло, як на наступному зображенні? [Підказка: це чудовий момент для використання функцій формування.]

• Прочитайте книгу Джозефа Альберса "Взаємодія кольору" і скористайтеся для практики наведеними нижче прикладами шейдерів.

Примітка про функції та аргументи

Перш ніж перейти до наступного розділу, зупинімось і трохи перемотаємо назад. Поверніться та погляньте на функції в попередніх прикладах. Ви можете помітити слово in перед типом аргументів. Це кваліфікатор, і в цьому випадку він вказує, що змінна лише для читання. У наступних прикладах ми побачимо, що також можна визначити аргументи із кваліфікаторами out або inout. Цей останній, inout, концептуально подібний до передачі аргументу за посиланням, що дає нам можливість змінювати передану змінну.

int newFunction(
    in vec4 aVec4,      // лише для читання
    out vec3 aVec3,     // лише для запису
    inout int aInt      // і для читання і для запису
);

Ви можете не повірити, але тепер у нас є всі необхідні елементи для створення крутих зображень. У наступному розділі ми навчимося комбінувати всі ці трюки, щоб створити геометричні фігури шляхом змішування простору. Так-так... змішування простору!