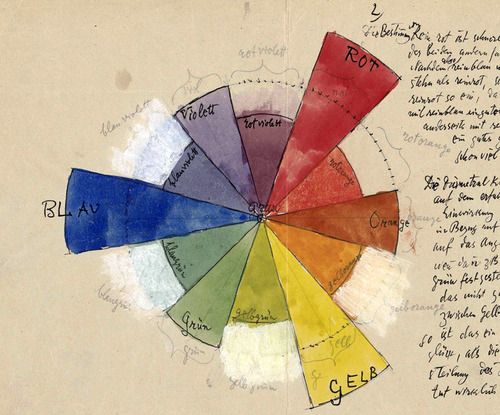
색상

그동안 GLSL 벡터 타입에 대해 자세히 이야기 할 기회가 별로 없었다. 진도를 더 나아가기 전에 변수와 색에 대해 더 많이 배우는 것이 GLSL 벡터를 이해하는데에 도움이 될 것 이다. 객체 지향 프로그래밍에 익숙하다면, 일반적인 C 구조체처럼 벡터 내부의 데이터에 접근해왔다는것을 눈치 챘을 것 이다.

vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

x, y, z 표기법을 사용하여 색을 정의하는 것은 혼란스럽고 오해의 소지가 있을 수 있다. 그렇지 않은가?
때문에 다른 표기법으로 동일한 정보에 액세스할 수 있는 방법들이 있다.
.x, .y, .z의 값은 .r, .g, .b 혹은 .s, .t, .p 라고도 할 수 있다.(일반적으로 .s, .t, .p는 다음 장에서 확인할 수 있는 텍스쳐의 공간 좌표에 사용된다.) 벡터 데이터에 인덱스 방식인 [0], [1], [2]으로도 접근할 수 있다.
다음 줄은 동일한 데이터에 액세스하는 모든 방법을 보여준다.

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

이러한 다양한 방법들은 명확한 코드를 작성하도록 설계된 명명법에 불과하다.
Shading language에 포함된 이러한 유연성은 "색상"과 "공간 좌표"에 대해 번갈아 생각할 수 있는 문을 열어준다.

GLSL 벡터의 또 다른 큰 특징은 원하는 순서로 속성을 조합할 수 있고, 따라서 값을 쉽게 캐스팅하고 혼합할 수 있다.
이것을 swizzle(뒤섞기) 이라고 한다.

vec3 yellow, magenta, green;

// 노란색 
yellow.rg = vec2(1.0);  // 빨강,초록 채널에 1.0 할당
yellow[2] = 0.0;        // 파랑 채널에 0.0 할당

// 마젠타색
magenta = yellow.rbg;   // 초록과 파랑채널을 교환

// 초록색
green.rgb = yellow.bgb; // 노란색의 파랑채널(0)을 빨강과 파랑채널에 할당.

색상 혼합

이제 색이 어떻게 정의되는지 알았으니, 이것을 지금까지 배운것들과 통합할 때이다. GLSL에는 두 값을 백분율로 혼합할 수 있는 매우 유용한 함수인 mix() 라는것이 있다.
백분율 범위가 얼마나 되는지 추측할 수 있는가? 그렇다, 바로 0.0 과 1.0 사이의 값이다!
긴 시간 동안 담장을 끼고 가라데를 연습한 당신에게 완벽한 것, 이제 이런 것들을 사용할 때이다!

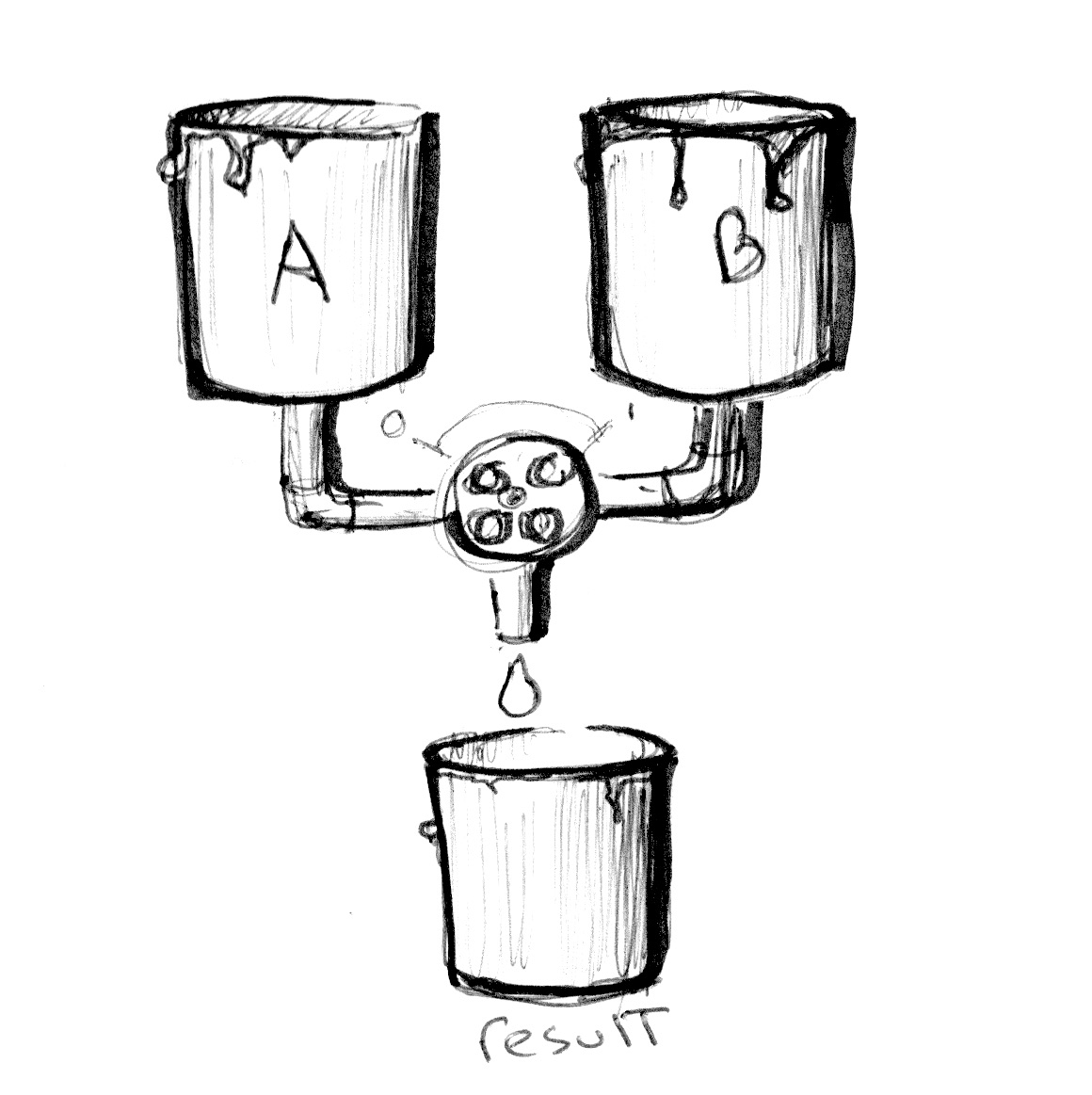
아래 코드의 18번째 줄에서 시간 경과에 따른 사인파의 절대값을 사용하여 colorA와 colorB를 혼합하는 방법을 확인해보시오.

다음 방법으로 여러분의 기술을 뽐내보시오:

• 색 사이를 표현적으로 전환해보아라. 특정 감정을 생각해 보아라. 그 감정을 표현하는 색은 무엇인가? 어떻게 보이는가? 어떻게 사라지나? 또다른 감정과 그것에 어울리는 색을 생각해 보시오. 위의 코드에서 시작 색과 끝 색을 해당 감정들과 일치하도록 변경해보시오. 그런 다음 Shaping functions(쉐이핑 함수)을 사용하여 애니메이션을 만들어보시오.
  Robert Penner는 easing functions 를 개발하였는데, 이는 애니메이션을 위해 자주사용되는 일련의 "Shaping functions(쉐이핑 함수)"의 모음집이다. 당신은 이 예시들을 연구와 영감을 위해 사용할 수 있지만, 최고의 결과는 자신만의 transitions 만들어봄으로써 나타날 것이다.

그라디언트 활용

mix() 함수는 더 많은 기능을 제공한다. 단일 float 대신, 처음 두 변수와 일치하는 변수 유형을 전달할 수 있는데, 우리의 예시는 vec3 이다. 이로써 각 개별 색상 채널 r, g, b의 혼합 비율을 제어할 수 있다.

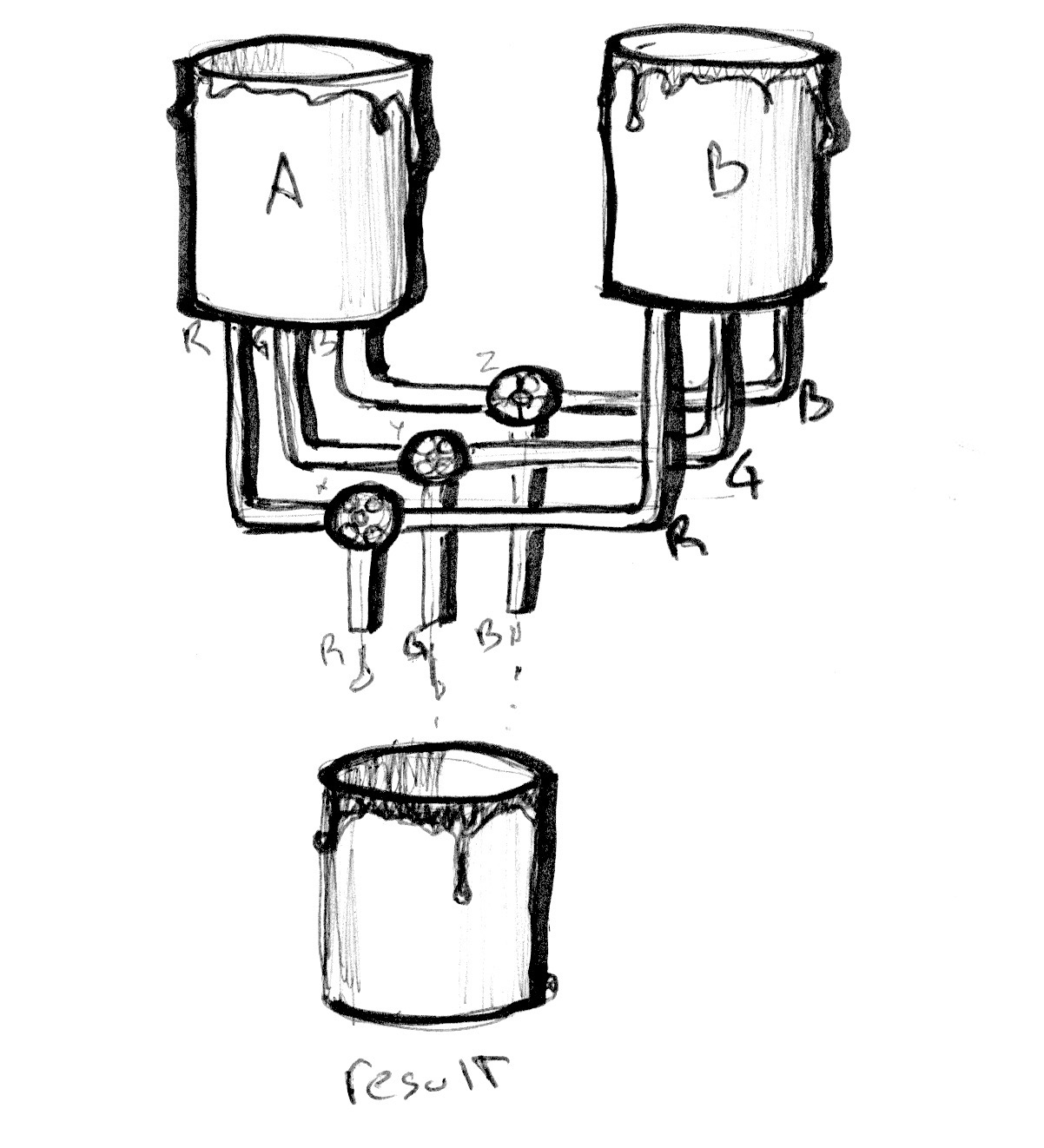
다음 예를 살펴보아라. 앞 장의 예와 같이, 정규화된 x 좌표로 전환하고 선으로 시각화하고 있다.
이제 모든 채널들이 같은 선을 따라가고 있다.

자, 25번줄을 주석해제하고 무슨 일이 일어나는지 보아라. 26번과 27번 라인의 주석도 해제해보아라.
선은 채널당 혼합할 colorA와 colorB의 양을 시각화한다는것을 기억해라.

다음 연습들을 해 보세요. 아마 당신은 25-27 줄에서 사용하고 있는 세 가지 쉐이핑 함수를 인지했을 것이다. 이것들을 갖고 놀아보아라!
이제 여태까지 배운 스킬을 탐색하고 뽐내며 흥미로운 Gradient를 만들 때이다.
다음 연습들을 해 보아라:

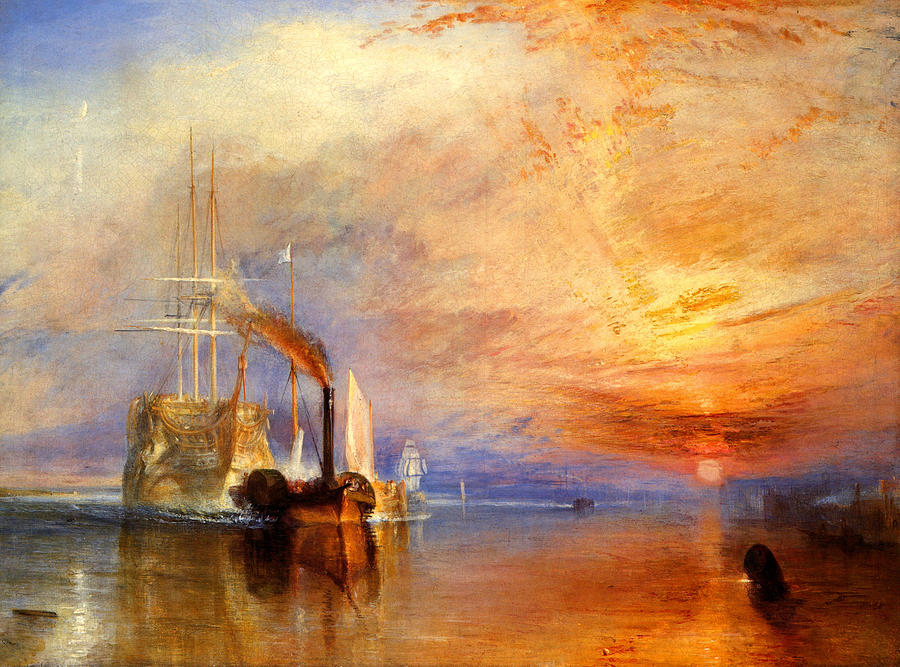
• William Turner sunset을 닮은 그라디언트를 구현해보기

• u_time을 사용하여 일출과 일몰 사이의 전환 애니메이션 만들기

• 지금까지 배운 것을 이용해 무지개를 만들 수 있는가?

• step()을 사용하여 컬러 플래그 만들기

HSB

색 공간에 대해 모르고서는 결코 색을 논할 수 없다. 아시다시피 빨강,초록,파랑 채널 외에도 색을 구성하는 방법은 다양하다.

HSB는 Hue, Saturation, Brightness(또는 Value)의 약자로, 더욱 직관적이고 유용한 색 공간이다.
잠시 시간을 내어 다음 코드에서 rgb2hsv() 및 hsv2rgb() 함수를 읽어 보아라.

x축의 위치를 Hue에 대응시키고 y축의 위치를 Brightness에 대응시킴으로써 우리는 가시적인 색상의 멋진 스펙트럼을 얻는다. 이러한 색상의 공간적 분포는 매우 편리하다; RGB보다 HSB로 색을 선택하는 것이 더 직관적일 수 있다.

극좌표계에서의 HSB

HSB 공간은 원래 데카르트 좌표(x와 y 기준) 대신 극 좌표(각도와 반지름 기준)로 표시되도록 설계되었다.
HSB 함수를 극좌표에 대응시키려면 빌보드의 중심에서 픽셀 좌표까지의 각도와 거리를 구해야 한다.
이를 위해 length() 함수와 atan(y,x) (일반적으로 사용되는 atan2(y,x)의 GLSL 버전)을 사용할 것이다.

벡터와 삼각함수를 사용할 때, vec2, vec3, vec4는 색을 나타낼 때도 벡터로 간주된다.
우리는 색과 벡터를 비슷하게 다루기 시작할 것이고, 이러한 개념적 유연성이 여러분의 실력을 키워준다는것을 알게 될 것이다.

참고: 다음과 같이, length 와 비슷한 많은 기하학적 함수들이 있다:
distance(), dot(), cross, normalize(), faceforward(), reflect(), refract().
또한 GLSL에는 다음과 같은 특수한 벡터 관계 함수들이 있다:
lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal(), notEqual().

각도와 길이를 파악한 후에는 값을 0.0~1.0 범위로 "정규화"해야 한다. 27행에서 atan(y,x)는 -PI와 PI 사이(-3.14~3.14)의 라디안의 각도를 반환하므로, 이 숫자를 TWO_PI(코드 상단에 정의됨)로 나누어 값을 -0.5~0.5 사이로 가져와 원하는 범위인 0.0~1.0으로 변경한다. 반지름은 최대 0.5를 반환하므로(뷰 포트의 중심에서 거리를 계산하기 때문에) 이 범위를 두 배로 늘려야 최대 1.0을 얻을 수 있다.

보시다시피, 지금 이 게임은 우리가 좋아하는 0.0에서 1.0까지의 범위를 변환하고 매핑하는 것이 전부이다.

다음 연습들을 해 보아라:

• polar예제를 회전판색상으로 수정해보기, Mac의 대기 중 마우스 아이콘 처럼

• HSB에서 RGB로의 변환 함수와 함께 쉐이핑 함수를 사용하여 특정 색조 값을 확장하고 나머지는 축소해보기.

• 컬러 픽커에 사용되는 컬러휠을 자세히 살펴보면(아래 이미지 참조), RYB 컬러 공간에 의한 다른 스펙트럼을 사용한다.
  예를 들어, 빨간색의 보색은 녹색이어야 하지만, 우리의 예에서는 청록색이다. 다음 이미지와 똑같이 보이도록 수정해볼 수 있는가? [힌트: 쉐이핑 함수를 사용해보기 좋은 예시 이다.]

• Josef Albers의 책 "색채의 상호작용"을 읽고 다음 Shader 예제를 연습으로 사용해보시오.

함수 및 매개변수에 대한 참고

다음 장으로 뛰어들기 전에, 잠시 멈추고 복습을 해보자.
이전 예제들로 돌아가서 함수들을 한 번 살펴보아라. 매개변수 전에 위치한 in이라는 키워드가 보일 것이다. 이는 해당 변수가 읽기 전용인지 지정하는 qualifier(수식어)이다. 앞으로 나올 예시에서는 out이나 inout도 나올 것 이다. 마지막인 inout은 전달된 변수를 수정할 수 있는 방식인 참조를 통해 인수를 전달하는 것과 개념적으로 유사하다.

int newFunction(in vec4 aVec4,      // 읽기전용(read-only)
                out vec3 aVec3,     // 쓰기전용(write-only)
                inout int aInt);    // 읽기-쓰기(read-write)

믿기지 않겠지만, 이제 우리는 멋진 그림을 그릴 수 있는 모든 것을 배웠다. 다음 챕터에서는 공간을 혼합(blending) 하여 기하학적 형태를 만들기 위해 우리의 모든 기술을 조합하는 방법을 배울 것입니다. 그렇다... 공간을 혼합한다.