Couleurs

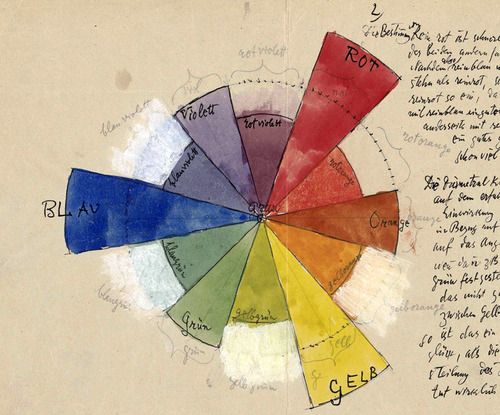
Jusqu'ici, nous avons manipulé des vecteurs mais nous n'avons pas encore pris le temps de voir comment marchent ces variables. Avant d'aller plus loin, il est important d'en savoir plus sur ces variables. Aborder la couleur est un bon moyen de se pencher sur la question.

Si vous connaissez la Programmation Orientée Objet, vous aurez remarqué que nous accédons aux données des vecteurs comme on le ferait avec des struct en C, grâce à des accesseurs / mutateurs (getters / setters en anglais).

Bien que cette pratique soit méconnue, il est possible d'utiliser des struct en GLSL, plus d'informations ici.

vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

Dans l'exemple ci dessus, x, y et z permettent d'accéder aux 3 valeurs contenues dans l'objet red de type vec3, ce sont les accesseurs aux propriétés de red.

Définir une couleur avec x, y et z peut être un peu déroutant, c'est pourquoi il existe différentes manières d'accéder aux valeurs des propriétés des vecteurs. Les valeurs de .x, .y et .z peuvent être récupérées avec les accesseurs .r, .g et .b, ou .s, .t et .p. (.s, .t et .p sont généralement utilisées pour encoder les coordonnées spatiales des textures, nous verrons ça dans les chapitres suivants). Il est également possible d'accéder aux valeurs des propriétés des vecteurs par leur position d'index dans l'objet: [0], [1] and [2].

Les lignes suivantes montrent les différentes manières d'accéder aux données :

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

On peut les utiliser ces accesseurs de façon indépendante ; le code suivant crée un clone newColor du vecteur color en utilisant chaque fois un accesseur différent.

vec4 color = vec4( 1.,0.,0.5,1. );
vec4 newColor = vec4( color[0], color.g, color.z, color.q );

Il est possible de combiner les propriétés en concaténant les accesseurs : si on veut exploiter les valeurs .r, .g et .b d'un vecteur 4 sans se soucier de .a (l'alpha), on peut écrire :

vec4 color = vec4( 1.,0.,0.5,1. );
vec4 newColor = vec4( color.rgb, 1.0 );

Ce qui revient à cloner chaque proriété .r, .g et .b du vecteur color sauf la dernière .a.

Dans ce cas, color.rgb est interprété comme un vecteur de type vec3 et il contient les valeurs .r, .g et .b du vec4 color. De même, si on écrit:

vec4 color = vec4( 1.,0.,0.5,1. );
vec3 newColor = vec3( color.xy, 1.0 );

On va utiliser les valeurs .x et .y de color pour construire un vec3 dont les valeurs .r et .g seront les mêmes que les valeurs .r et .g du vecteur color et où la valeur .b sera 1.0.

Dernière chose, l'ordre dans lequel on concatène les accesseurs est important. Si on veut construire un vecteur à partir d'un autre mais en inversant l'ordre des propriétés, on peut l'écrire comme suit :

vec3 color = vec3( 1.0, 0.0, 0.5 );
vec3 newColor = color.bgr;

le vecteur newColor va copier les propriétés de color mais au lieu de les copier dans l'ordre "normal":.r, .g et .b, il va les copier dans l'ordre inverse: .b, .g et .r.

color.r = 1.0
color.g = 0.0
color.b = 0.5
// et
newColor.r = 0.5
newColor.g = 0.0
newColor.b = 1.0

Il en découle que si les déclarations suivantes sont équivalentes :

color.rgba = color.xyzw = color.stpq

Ces déclarations ne le sont pas :

color.rgba != color.argb != color.rbga != color.abgr // etc.
color.xyzw != color.wxyz != color.xzyw != color.wzyx // etc.
color.stpq != color.qstp != color.sptq != color.qpts // etc.

C'est une fonctionnalité très puissante ; elle permet de stocker les informations dans un format compact. Un exemple d'utilisation, si on veut décrire un rectangle, on peut se servir soit de 2 vec2 décrivant respectivement le coin supérieur gauche et le coin inférieur droit, ou bien, utiliser un seul vec4 dont l'accesseur .xy renverra un vec2 décrivant le coin supérieur gauche, et l'accesseur .zw renverra un vec2 décrivant le coin inférieur droit.

Ces différentes manière d'accéder aux variables à l'intérieur des vecteurs sont simplement là pour nous aider à écrire un code lisible.

Cette souplesse d'utilisation est le point d'entrée qui vous permettra de penser aux espaces cartésiens (le "vrai" espace) et colorimétriques de façon interchangeable.

La concaténation prend tout son sens lorsqu'on veut pouvoir combiner des vecteurs dans un ordre arbitraire pour les mélanger (cette propriété s'appelle le swizzle).

vec3 jaune, magenta, vert;

// crée le jaune
jaune.rg = vec2(1.0);  // Assigne 1. au canaux rouges et vert du vecteur jaune
jaune[2] = 0.0;        // Assigne 0. au canal bleu du vecteur jaune

// crée le magenta
magenta = jaune.rbg;   // Assigne the valeur en intervertissant le vert et le bleu ( rbg au lieu de rgb )

// crée le vert
vert.rgb = jaune.bgb; // Assigne le canal bleu du jaune (0) aux canaux rouges et bleus

Mélanger les couleurs

A présent que nous savons définir les couleurs, il est temps de les utiliser avec ce que nous avons déjà appris.

En GLSL, il existe une fonction extrêmement utile mix(), qui permet de mélanger deux valeurs en fonction d'un pourcentage.

Comme vu au chapitre précédent, mix() permet d'interpoler entre 2 valeurs grâce à une troisième valeur T. Exactement comme smoothstep() à la différence que cette fois, la fonction mix() prend en argument des vecteurs au lieu de floats.

Pouvez vous deviner ce que devra être le pourcentage ? Evidemment, une valeur normalisée entre 0.0 et 1.0 ! Ce qui nous va très bien, après tout ce temps passé sur la palissade du chapitre précédent, il est enfin temps de frapper !

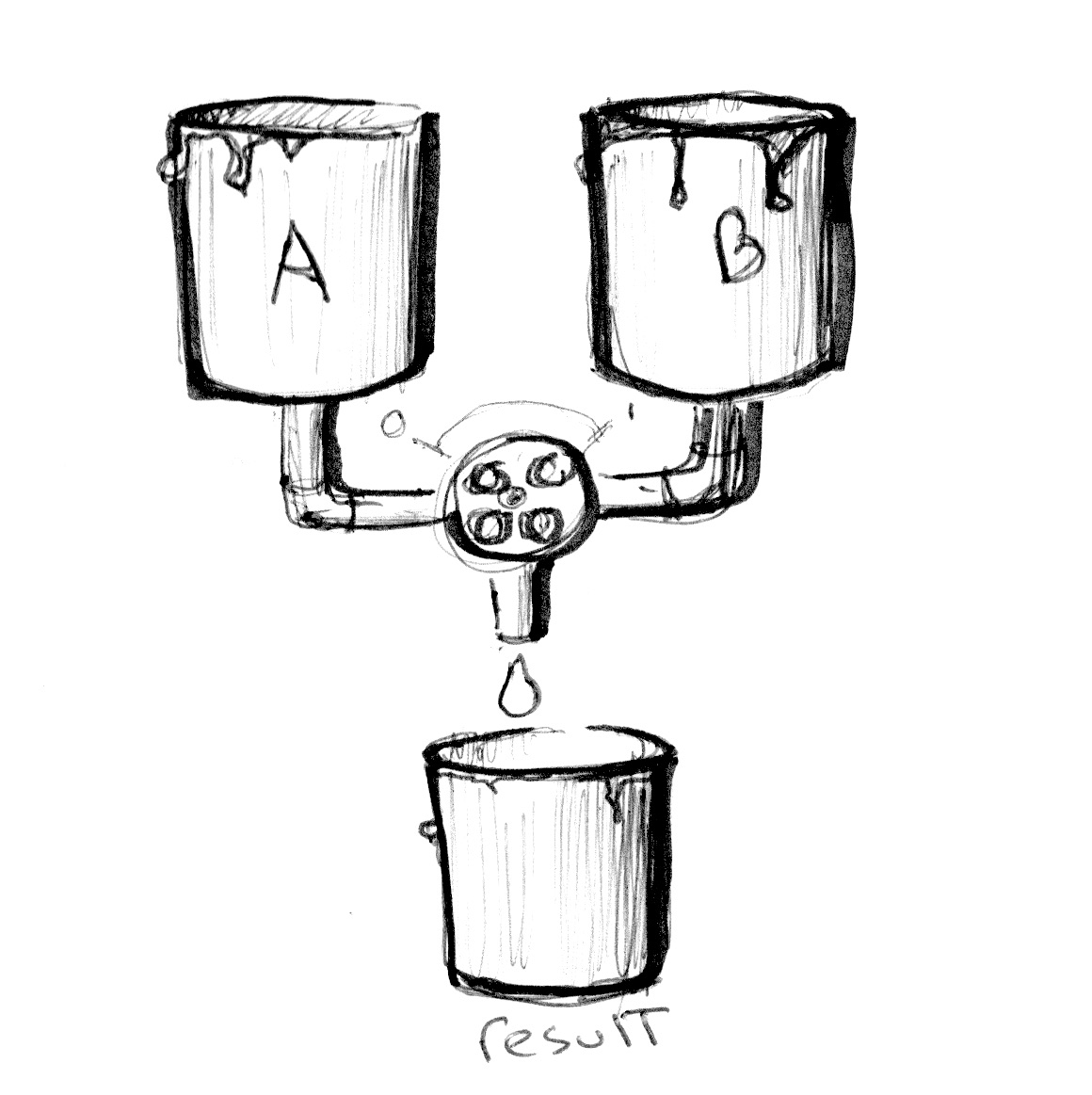
Observez la ligne 18: notez que nous utilisons la valeur absolue (abs()) d'une fonction de sinus (sin()) prenant le temps en argument pour contrôler le mélange entre colorA et colorB.

Montrez de quoi vous êtes capable :

• Créez une transition expressive entre les couleurs. Pensez à une émotion en particulier.
• Quelle couleur représente le mieux cette émotion ? Comment apparaît-elle ? Comment disparaît-elle ?
• Pensez à une autre émotion et à la couleur correspondante, changez les couleur A et B dans le code puis utilisez les fonctions de formes pour opérer la transition.

Robert Penner a développé une série de fonctions destinées à créer des animations, connues sous le nom d'easing functions. Vous pouvez utiliser cet exemple comme base de recherche mais les meilleures transitions seront celles que vous ferez vous mêmes.

Jouer avec les dégradés

La fonction mix() peut faire plus. Au lieu de passer un seul float pour faire l'interpolation, nous pouvons passer successivement plusieurs valeurs de transition. Dans l'exemple suivant, nous passons les valeurs r, g et b d'un vec3 (pct pour pourcentage) pour contrôler le mélange des canaux.

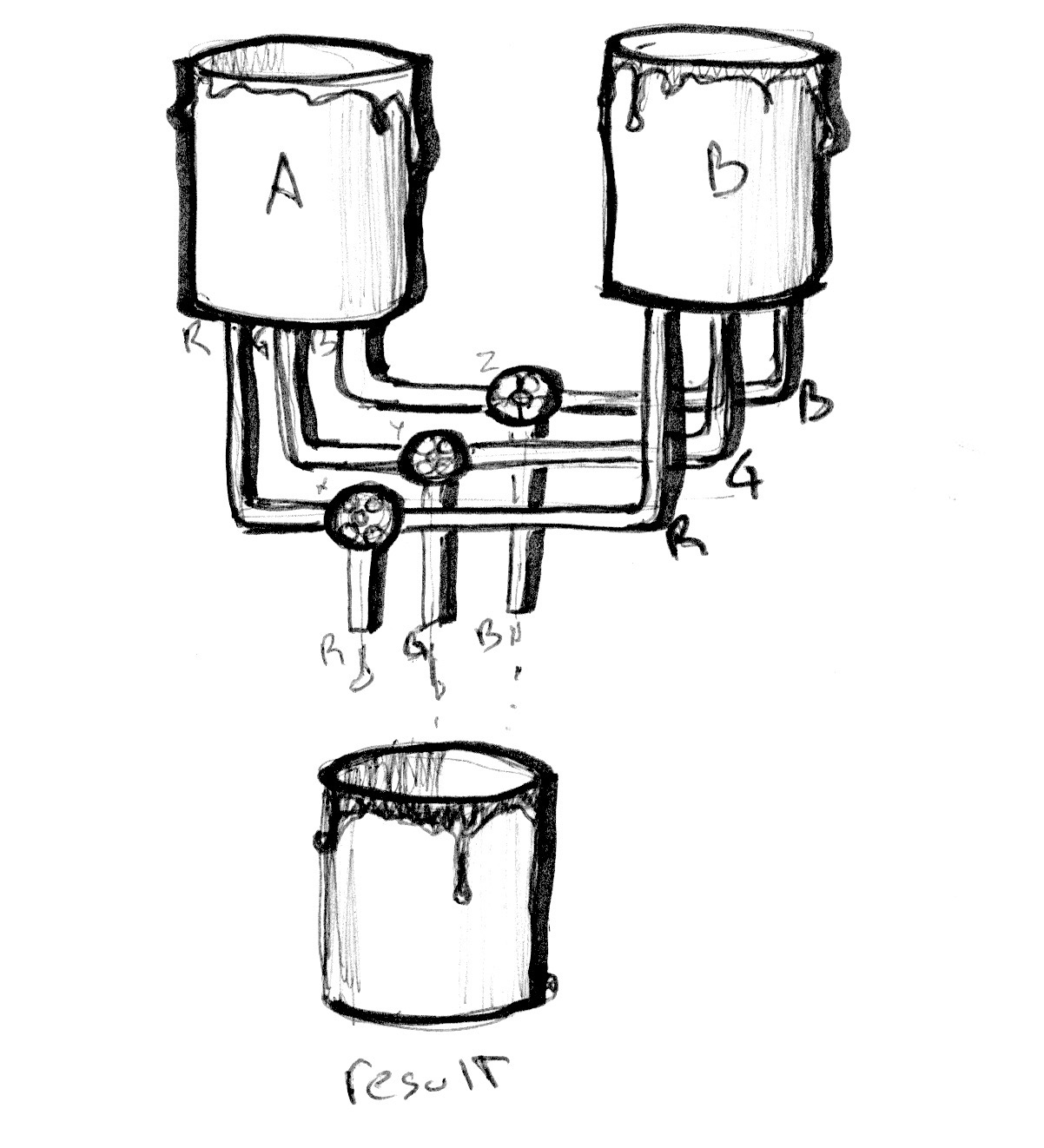
Regardez l'exemple suivant. Comme au chapitre précédent, nous branchons la valeur de transition sur la valeur normalisée de x et nous la visualisons par une ligne. Au début, rien d'exceptionnel, le dégradé est linéaire sur les trois canaux.

A présent, décommentez la ligne 25 et regardez ce qui se passe, puis décommentez les lignes 26 et 27. Rappelez vous que les lignes représentent la quantité de mélange entre colorA et colorB par canal de couleur.

Vous aurez sans doute reconnu les 3 fonctions de forme du chapitre précédent aux lignes 25, 26, 27. A vous de jouer ! Il est temps d'explorer et de créer des dégradés intéressants en ré-utilisant ce que nous avons vu au chapitre précédent. Essayez les exercices suivants :

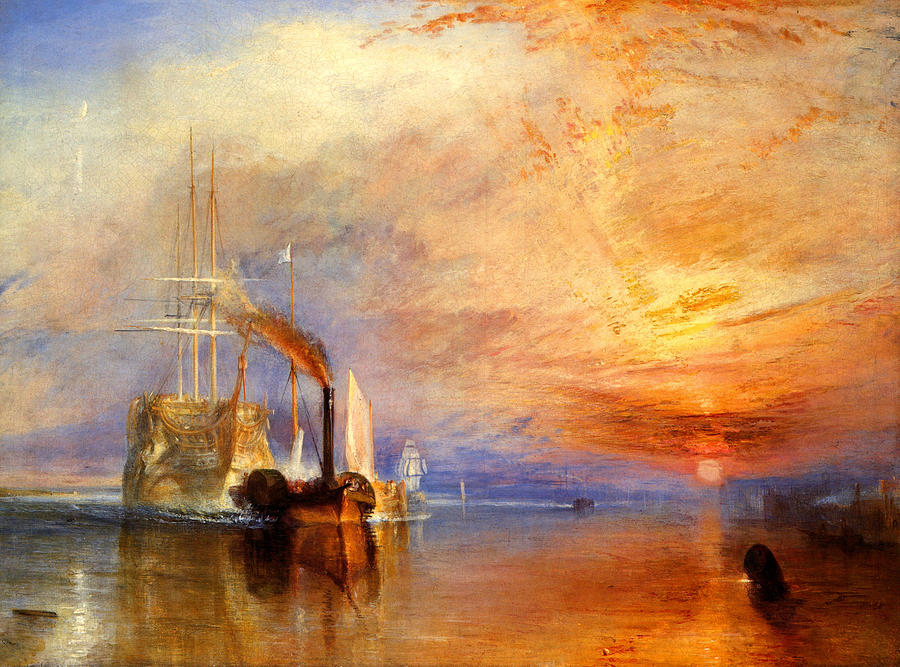
• Composez un dégradé qui ressemble au coucher de soleil ci-dessus.

• Animez une transition entre lever et coucher de soleil en utilisant u_time.

• Pouvez vous créer un arc-en-ciel avec ce que vous avez appris jusqu'à présent ?

• Utilisez la fonction step() pour créer un drapeau.

HSB

On ne peut pas parler de couleur sans parler d'espace colorimétrique. Vous le savez sans doute, il existe plusieurs façons d'organiser les canaux rouge, vert, bleu.

HSB signifie "Hue, Saturation, Brightness (ou Value)" soit en bon français "Teinte, Saturation, Luminosité", c'est une manière plus intuitive d'organiser les couleurs. Prenez un instant pour lire et essayer de comprendre les méthodes rgb2hsv() et hsv2rgb() dans le code suivant.

En indexant la Teinte (Hue) sur la position en x et la Luminosité (Brigthness) sur la position en y, nous obtenons un spectre des couleurs complet. Cette distribution spatiale des couleurs peut être très pratique ; il est plus simple de choisir une couleur dans un espace HSB que dans un espace RGB.

HSB et coordonnées polaires

A l'origine, HSB a été conçu pour être représenté dans un système de coordonnées polaires. Par opposition à un système de coordonnées cartésien décrit par 2 axes X et Y orthogonaux, un système de coordonnées polaires, est décrit par des angles et des rayons. Pour dessiner notre fonction HSB, nous devons obtenir la position du centre du canvas de manière à connaître l'angle et la distance de chaque fragment au centre. Pour cela nous allons utiliser la méthode length() et atan(y,x) qui est l'équivalent GLSL de la méthode atan2(y,x).

Lorsqu'on utilise des vecteurs avec des fonctions trigonométriques les variables de type vec2, vec3 et vec4 sont considérées comme des vecteurs géométriques même si elles représentent des couleurs. Nous commencerons à traiter les couleurs et les vecteurs géométriques de façon similaire, en fait, vous devriez comprendre assez vite que cette flexibilité d'utilisation est une force.

Note : Si vous vous demandez s'il existe d'autres fonctions géométriques que length comme : distance(), dot(), cross, normalize(), faceforward(), reflect() et refract(), la réponse est oui. GLSL expose également des méthodes pour comparer les vecteurs entres eux : lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() et notEqual().

Une fois que nous avons récupéré l'angle entre le centre et le fragment en cours, nous devons le normaliser. Ligne 27, atan(y,x) nous retourne un angle en radians compris entre -PI et PI (~-3.14 to ~3.14), pour le normaliser, nous devons diviser cet angle par 2 x PI, la macro TWO_PI en début de code nous permet de stocker cette valeur. En divisant l'angle par TWO_PI, nous obtenons un chiffre compris entre -0.5 (-PI / TWO_PI) et 0.5 (PI / TWO_PI) auquel il nous suffit d'ajouter 0.5 pour qu'il soit compris entre 0.0 et 1.0.

Le rayon (la distance du centre au fragment) retournera une valeur max de 0.5 en x et en y (parce que nous calculons la distance depuis le centre du canvas), nous devons donc doubler cette valeur (en la multipliant par 2) pour obtenir un rayon compris entre 0.0 et 1.0.

Vous voyez que tout est question de ramener les valeurs dans l'espace entre 0.0 et 1.0, un espace normalisé.

Essayez les exercices suivants :

• Modifiez l'exemple des coordonnées polaires pour faire tourner les couleurs.

• Utilisez les fonctions de formes avec les fonctions de conversion HSB vers RGB pour étendre une valeur de teinte spécifique et rétrécir le reste.

• Si vous regardez attentivement la roue des couleurs qu'utilisent les sélecteurs de couleurs (voir l'image ci-dessous), ils affichent un spectre différent basé sur du RYB. Par exemple, la couleur opposée au rouge devrait être le vert mais dans nos exemples, c'est le Cyan. Pouvez vous trouver un moyen d'arranger ça de manière à obtenir exactement le meme rendu que sur l'image ? Indice: c'est un bon moment pour vous servir des fonctions de formes.

• Lisez le livre de Josef Albers : L'Interaction des Couleurs et servez vous des exemples suivants pour vous entraîner à reproduire ses exemples.

A propos des fonctions et des arguments

Avant de passer au chapitre suivant, attardons nous un peu sur les fonctions du dernier exemple. Vous remarquerez un in avant les types des arguments. C'est ce qu'on appelle un qualifier et dans ce cas précis, cela signifie que la variable est en lecture seule. Dans les exemples suivants, nous verrons qu'il est également possible de donner les qualifiers out et inout aux variables passées aux fonctions. Cette dernière, inout, est équivalente à passer un argument par référence en C ; cela nous donne la possibilité de modifier la valeur de la variable passée en argument.

int newFunction(in vec4 aVec4,      // lecture seule
                out vec3 aVec3,     // écriture seule
                inout int aInt);    // lecture / écriture

Vous ne le savez pas encore et vous pourriez ne pas le croire mais nous avons à présent tout ce qu'il nous faut pour dessiner à peu près n'importe quoi. Au prochain chapitre, nous verrons comment combiner ces techniques pour mélanger l'espace. Oui... mélanger l'espace !