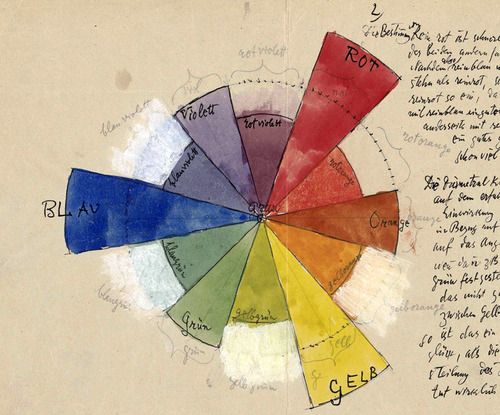
Warna

Kami tidak memiliki banyak kesempatan untuk membicarakan jenis vektor GLSL. Sebelum melangkah lebih jauh, penting untuk mempelajari lebih lanjut tentang variabel-variabel ini dan subjek warna adalah cara yang bagus untuk mengetahuinya lebih lanjut.

Jika Anda terbiasa dengan paradigma pemrograman berorientasi objek, Anda mungkin memperhatikan bahwa kami telah mengakses data di dalam vektor seperti struct biasa mirip-C.

vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

Mendefinisikan warna menggunakan notasi x, y dan z bisa membingungkan dan menyesatkan, bukan? Itulah mengapa ada cara lain untuk mengakses informasi yang sama ini, tetapi dengan nama yang berbeda. Nilai dari .x,.y dan .z juga bisa disebut.r, .g dan.b, dan .s,.t dan .p. (.s,.t dan .p biasanya digunakan untuk koordinat spasial suatu tekstur, yang akan kita lihat di bab selanjutnya.) Anda juga dapat mengakses data dalam vektor dengan menggunakan posisi indeks , [0], [1] dan [2].

Baris berikut menunjukkan semua cara untuk mengakses data yang sama:

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

Cara berbeda untuk menunjuk ke variabel di dalam vektor hanyalah tata nama yang dirancang untuk membantu Anda menulis kode yang jelas. Fleksibilitas yang tertanam dalam bahasa shading ini merupakan pintu bagi Anda untuk mulai berpikir secara bergantian tentang warna dan koordinat ruang.

Fitur hebat lainnya dari jenis vektor di GLSL adalah bahwa properti dapat digabungkan dalam urutan apa pun yang Anda inginkan, yang memudahkan untuk mentransmisikan dan mencampur nilai. Kemampuan ini disebut swizzle.

vec3 yellow, magenta, green;

// Making Yellow
yellow.rg = vec2(1.0);  // Assigning 1. to red and green channels
yellow[2] = 0.0;        // Assigning 0. to blue channel

// Making Magenta
magenta = yellow.rbg;   // Assign the channels with green and blue swapped

// Making Green
green.rgb = yellow.bgb; // Assign the blue channel of Yellow (0) to red and blue channels

Mencampur warna

Sekarang setelah Anda mengetahui bagaimana warna didefinisikan, sekarang saatnya untuk mengintegrasikannya dengan pengetahuan kita sebelumnya. Di GLSL ada fungsi yang sangat berguna, mix(), yang memungkinkan Anda mencampur dua nilai dalam persentase. Bisakah Anda menebak berapa kisaran persentasenya? Ya, nilai antara 0,0 dan 1,0! Yang sempurna untuk Anda, setelah berjam-jam berlatih gerakan karate Anda dengan pagar - sekarang saatnya menggunakannya!

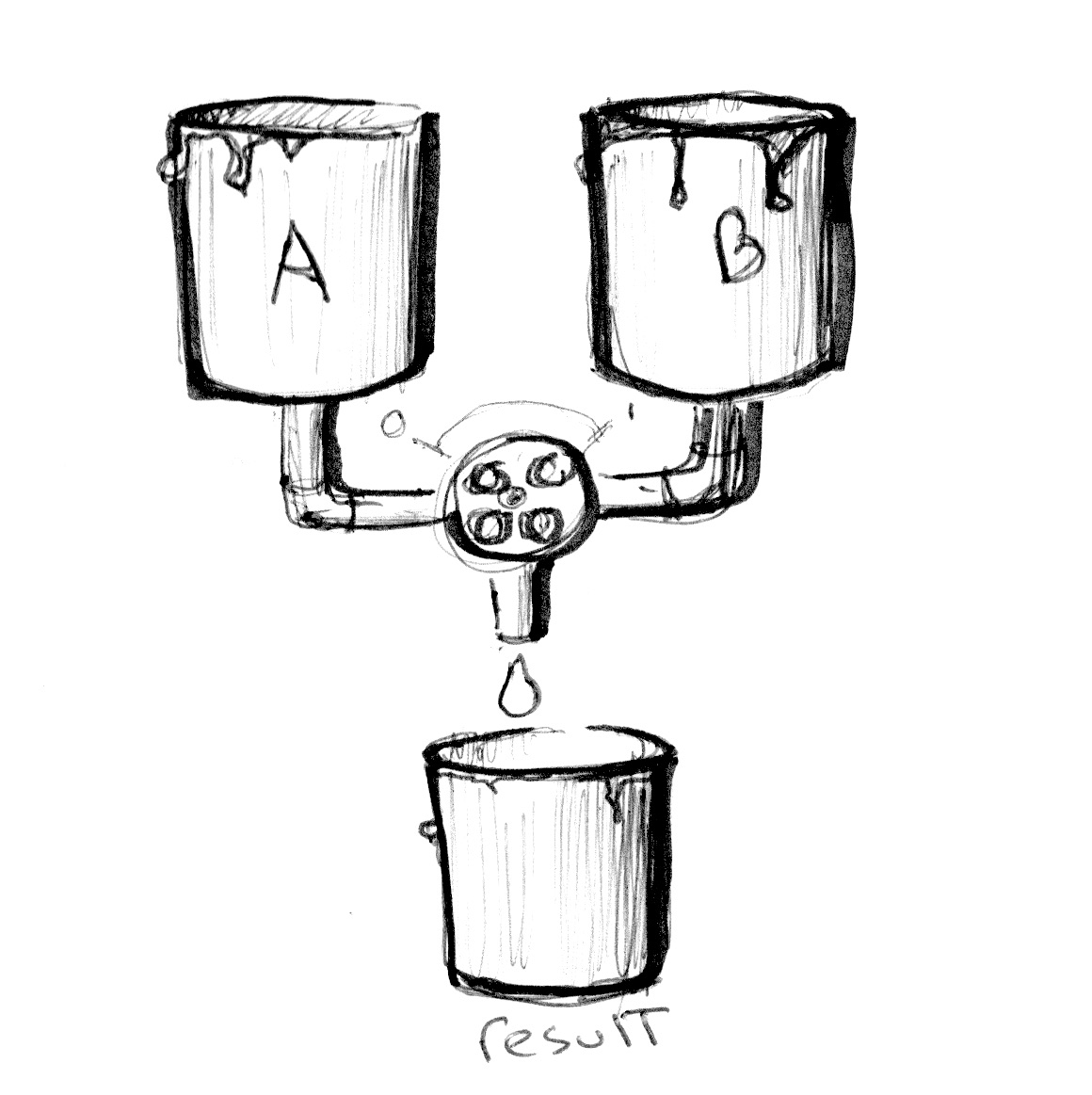
Periksa kode berikut pada baris 18 dan lihat bagaimana kita menggunakan nilai absolut gelombang sin dari waktu ke waktu untuk mencampur colorA dancolorB.

Pamerkan keahlian Anda dengan:

• Buat transisi ekspresif antar warna. Pikirkan emosi tertentu. Warna apa yang paling mewakili itu? Bagaimana tampilannya? Bagaimana cara memudar? Pikirkan emosi lain dan warna yang cocok untuknya. Ubah warna awal dan akhir kode di atas agar sesuai dengan emosi tersebut. Kemudian animasikan transisi menggunakan fungsi pembentuk. Robert Penner mengembangkan serangkaian fungsi pembentukan yang populer untuk animasi komputer yang dikenal sebagai fungsi pelonggaran, Anda dapat menggunakan contoh ini sebagai penelitian dan inspirasi tetapi hasil terbaik akan datang dari membuat transisi Anda sendiri.

Bermain dengan gradien

Fungsi mix () memiliki lebih banyak hal untuk ditawarkan. Alih-alih satu float, kita bisa meneruskan tipe variabel yang cocok dengan dua argumen pertama, dalam kasus kitavec3. Dengan melakukan itu kita mendapatkan kendali atas persentase pencampuran dari setiap saluran warna individual, r,g dan b.

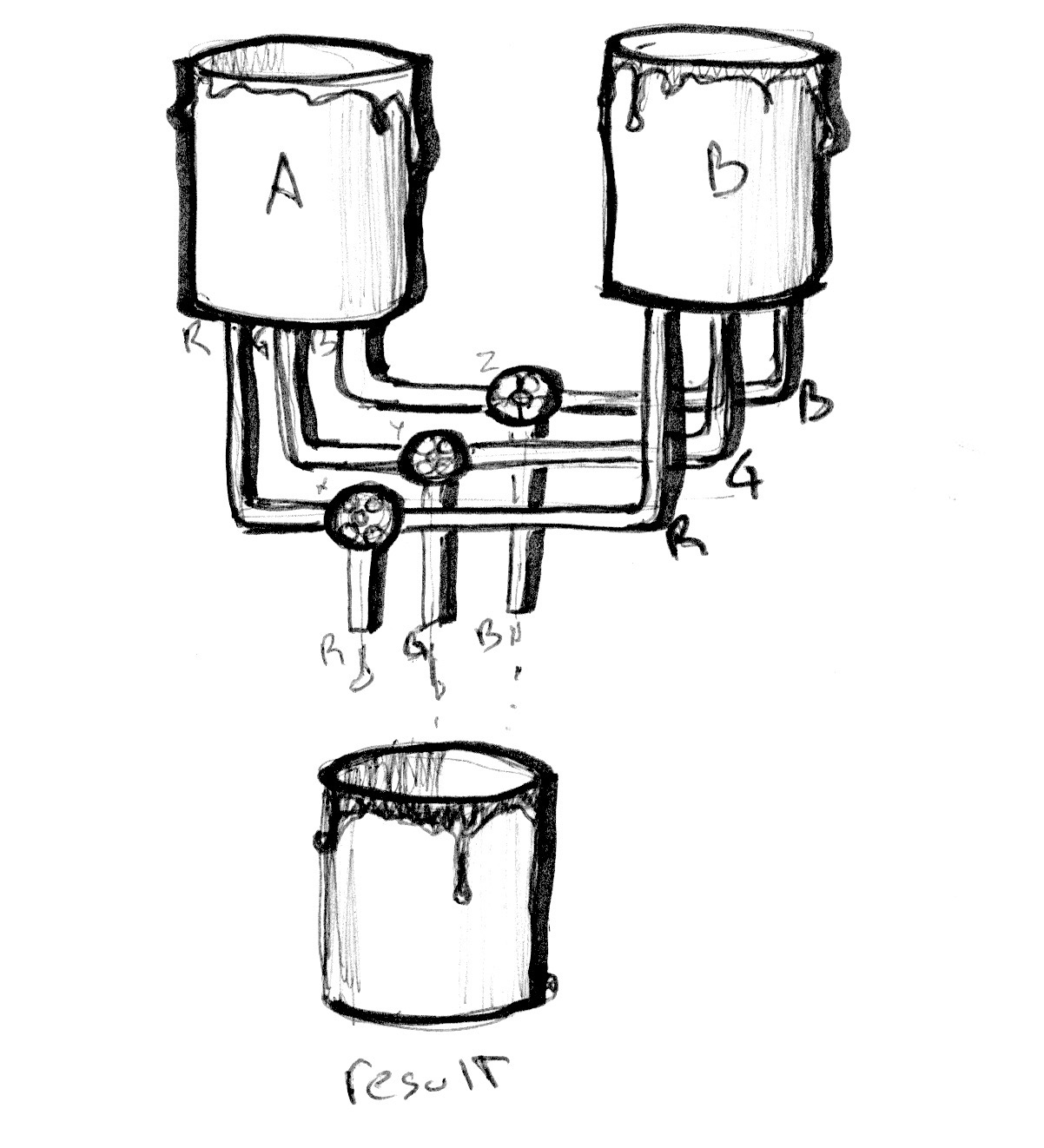
Lihat contoh berikut. Seperti contoh di bab sebelumnya, kami mengaitkan transisi ke koordinat x yang dinormalisasi dan memvisualisasikannya dengan garis. Saat ini semua saluran berada di jalur yang sama.

Sekarang, hapus komentar pada baris nomor 25 dan lihat apa yang terjadi. Kemudian coba hapus komentar pada baris 26 dan 27. Ingatlah bahwa baris memvisualisasikan jumlah colorA dancolorB yang akan digabungkan per saluran.

Anda mungkin mengenali tiga fungsi pembentuk yang kami gunakan pada baris 25 hingga 27. Mainkanlah dengan mereka! Saatnya bagi Anda untuk menjelajahi dan memamerkan keahlian Anda dari bab sebelumnya dan membuat gradien yang menarik. Coba latihan berikut:

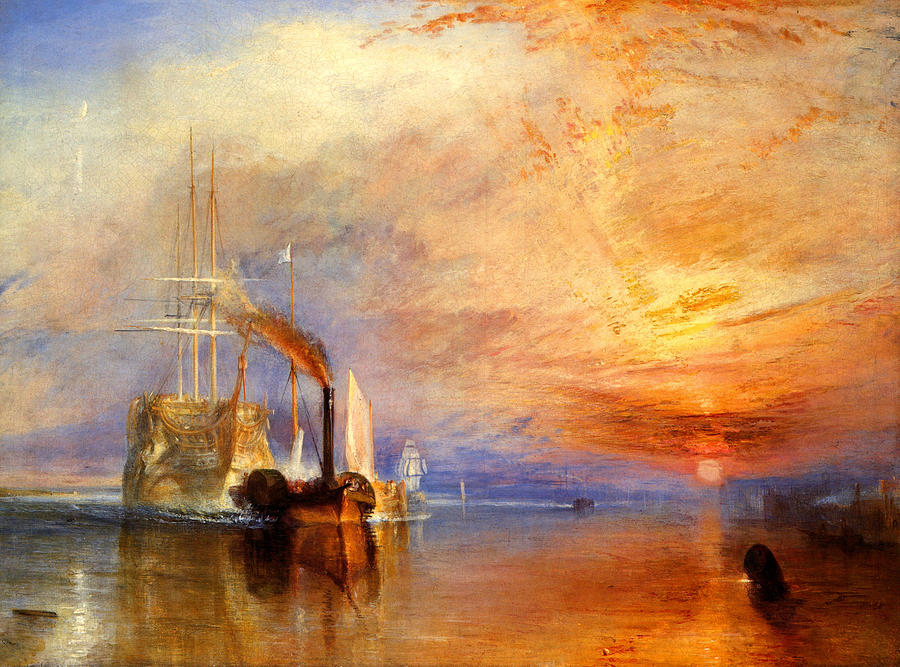
• Buat gradien yang menyerupai matahari terbenam William Turner

• Menganimasikan transisi antara matahari terbit dan terbenam menggunakan u_time.

• Bisakah Anda membuat pelangi menggunakan apa yang telah kita pelajari sejauh ini?

• Gunakan fungsi step() untuk membuat bendera warna-warni.

HSB

Kita tidak dapat berbicara tentang warna tanpa berbicara tentang ruang warna. Seperti yang mungkin Anda ketahui, ada beberapa cara berbeda untuk mengatur warna selain dengan saluran merah, hijau dan biru.

HSB adalah singkatan dari Hue, Saturation and Brightness (atau Value) dan merupakan organisasi warna yang lebih intuitif dan berguna. Luangkan waktu sejenak untuk membaca fungsi rgb2hsv() dan hsv2rgb() pada kode berikut.

Dengan memetakan posisi pada sumbu x ke Hue dan posisi pada sumbu y ke Brightness, kita mendapatkan spektrum warna yang terlihat bagus. Distribusi warna spasial ini bisa sangat berguna; lebih intuitif untuk memilih warna dengan HSB dibandingkan dengan RGB.

HSB dalam koordinat kutub

HSB awalnya dirancang untuk direpresentasikan dalam koordinat kutub (berdasarkan sudut dan jari-jari), bukan koordinat kartesius (berdasarkan x dan y). Untuk memetakan fungsi HSB kita ke koordinat kutub, kita perlu mendapatkan sudut dan jarak dari pusat billboard ke koordinat piksel. Untuk itu kita akan menggunakan fungsi length() dan atan(y, x) (yaitu versi GLSL dari atan2(y, x)) yang umum digunakan.

Saat menggunakan fungsi vektor dan trigonometri, vec2,vec3, dan vec4 dianggap sebagai vektor meskipun keduanya mewakili warna. Kami akan mulai memperlakukan warna dan vektor dengan cara yang sama, bahkan Anda akan menemukan fleksibilitas konseptual ini sangat memberdayakan.

Catatan: Jika Anda bertanya-tanya, ada lebih banyak fungsi geometris selain panjang seperti: distance(), dot(), cross, normalize(), faceforward(), reflect() and refract(). Also GLSL has special vector relational functions such as: lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() dan notEqual().

Setelah kita mendapatkan sudut dan panjang, kita perlu "menormalkan" nilainya ke kisaran antara 0,0 hingga 1,0. Pada baris 27, atan(y, x) akan mengembalikan sudut dalam radian antara -PI dan PI (-3.14 hingga 3.14), jadi kita perlu membagi angka ini oleh TWO_PI (didefinisikan di bagian atas kode) untuk mendapatkan nilai antara -0,5 hingga 0,5, yang dengan penambahan sederhana kita ubah ke kisaran yang diinginkan dari 0,0 hingga 1,0. Jari-jari akan mengembalikan maksimum 0,5 (karena kita menghitung jarak dari pusat viewport) jadi kita perlu menggandakan jarak ini (dengan mengalikan dua) untuk mendapatkan maksimum 1,0.

Seperti yang Anda lihat, permainan kami di sini adalah tentang mengubah dan memetakan rentang ke 0,0 hingga 1,0 yang kami sukai.

Coba latihan berikut:

• Ubah contoh kutub untuk mendapatkan roda warna yang berputar, seperti ikon mouse menunggu.

• Gunakan fungsi pembentukan bersama dengan fungsi konversi dari HSB ke RGB untuk memperluas nilai rona tertentu dan mengecilkan sisanya.

• Jika Anda melihat lebih dekat pada roda warna yang digunakan pada pemilih warna (lihat gambar di bawah), mereka menggunakan spektrum yang berbeda sesuai dengan ruang warna RYB. Misalnya, warna kebalikan dari merah harus hijau, tetapi dalam contoh kita itu adalah cyan. Dapatkah Anda menemukan cara untuk memperbaikinya agar terlihat persis seperti gambar berikut? [Petunjuk: ini adalah momen yang tepat untuk menggunakan fungsi pembentukan.]

• Baca buku Josef Albers 'Interaction of Color dan gunakan contoh shader berikut sebagai latihan.

Catatan tentang fungsi dan argumen

Sebelum melompat ke bab berikutnya, mari kita berhenti dan mundur. Kembali dan lihat fungsi di contoh sebelumnya. Anda akan melihat in sebelum jenis argumen. Ini adalah qualifier ​​dan dalam hal ini menetapkan bahwa variabel hanya-baca. Dalam contoh mendatang kita akan melihat bahwa dimungkinkan juga untuk mendefinisikan argumen sebagai out atauinout. Yang terakhir ini, inout, secara konseptual mirip dengan meneruskan argumen dengan referensi yang akan diberikan kami kemungkinan untuk memodifikasi variabel yang dilewatkan.

int newFunction(in vec4 aVec4,      // read-only
                out vec3 aVec3,     // write-only
                inout int aInt);    // read-write

Anda mungkin tidak percaya, tetapi sekarang kami memiliki semua elemen untuk membuat gambar yang keren. Pada bab selanjutnya kita akan belajar bagaimana menggabungkan semua trik kita untuk membuat bentuk geometris dengan memadukan ruang. Ya ... memadukan ruang.