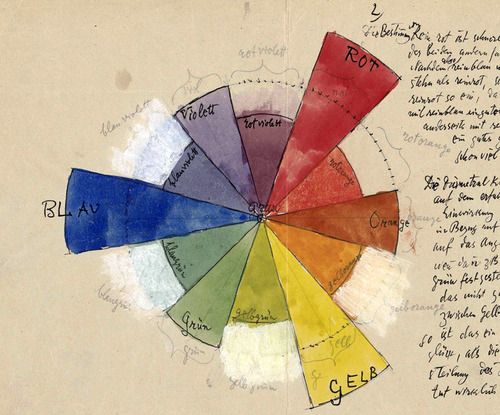
Màu sắc

Ta chưa đề cập nhiều lắm về các loại vector trong GLSL. Trước khi đi tiếp thì việc hiểu các kiểu dữ liệu này rất quan trọng và màu sắc là chủ đề phù hợp tuyệt vời để giải thích cho các khái niệm đó.

Nếu bạn đã quen với mô hình lập trình hướng đối tượng thì có thể bạn đã chú ý tới việc ta có thể truy cập dữ liệu bên trong các vector như cách mà struct của ngôn ngữ C làm việc.

vec3 red = vec3(1.0,0.0,0.0);
red.x = 1.0;
red.y = 0.0;
red.z = 0.0;

Định nghĩa một màu sử dụng các ký hiệu x, y và z có thể hơi khó hiểu nhỉ? Đó cũng chính là lý do mà ta sẽ có nhiều cách khác để truy cập dữ liệu trong vector. Các ký hiệu x, y và z có thể thay thế bằng .r, .g, .b, hoặc .s, .t, .p. (.s, .t và .p sẽ được sử dụng ở các chương sau để truy cập các toạ độ trong không gian của texture). Ngoài ra bạn cũng có thể truy cập các giá trị trong vector bằng vị trí trong array ([0], [1] và [2]).

Mỗi dòng code dưới đây đều truy cập một giá trị giống nhau trong vector:

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

Những cách truy cập khác nhau vào cùng 1 giá trị trong vector này sẽ giúp bạn viết code rõ ràng và dễ dàng hơn. Và sự linh hoạt này cũng sẽ khiến bạn dần dần xoá nhoà khoảng cách giữa không gian màu sắc và không gian vật lý, do chúng có cùng một cách lưu trữ dữ liệu.

Một tính năng khác cũng tuyệt vời không kém của vector trong GLSL là các giá trị bên trong có thể được tráo đổi (swizzle) vị trí theo bất kỳ trật tự nào bạn muốn, khiến cho việc xử lý chúng dễ dàng hơn bao giờ hết.

vec3 yellow, magenta, green;

// Tạo màu vàng (1., 1., 0.)
yellow.rg = vec2(1.0);  // Gán giá trị 1. cho kênh R và G
yellow[2] = 0.0;        // Gán giá trị 0. cho kênh B

// Tạo màu hồng (1., 0., 1.)
magenta = yellow.rbg;   // Đảo vị trí của 2 kênh G và B

// Tạo màu xanh lá (0., 1., 0.)
green.rgb = yellow.bgb; // Lấy giá trị ở kênh B của màu vàng để gán đồng thời cho cả kênh R và B của màu xanh lá

Trộn màu

Bạn đã biết cách định nghĩa các màu sắc rồi, giờ thì kết hợp nó với kiến thức đã có từ các chương trước nào. Trong GLSL có 1 hàm rất hữu ích, đó là mix(), giúp bạn trộn 2 màu với nhau theo 1 tỉ lệ nhất định. Và tỉ lệ đó cũng nằm trong khoảng [0.0, 1.0]. Hoàn hảo, đó chính là những gì mà ta đã học và luyện tập ở chương trước với việc sơn hàng rào, giờ thì lôi ra áp dụng thôi!

Hãy xem đoạn code dưới đây và chú ý vào dòng 18 vì tôi sẽ sử dụng giá trị tuyệt đối của đồ thị sóng hình sin làm tỉ lệ trộn 2 màu colorA và colorB.

Thử xem bạn thuần thục môn võ karate-shader đến đâu rồi nào:

• Hãy tạo một vùng chuyển tiếp mượt mà giữa 2 màu xem sao. Hãy sử dụng nó để diễn tả một cảm giác nào đó nhé. Màu gì thì diễn tả cảm giác đó tốt nhất? Nó xuất hiện rồi biến mất như thế nào? Rồi lại thử với một cảm giác khác. Sửa code để đổi 2 màu được chọn để trộn phía trên xem sao.
• Thay vì dùng hàm sin, hãy thử các hàm khác mà ta đã học ở chương trước xem sao
• Robert Penner đã phát triển một series các hàm số dùng trong animation rất nổi tiếng, chúng được gọi là các easing functions, bạn có thể sử dụng ví dụ này để tham khảo và lấy cảm hứng nhưng tốt nhất là bạn tự tạo ra dải màu gradient của riêng mình.

Gradient

Hàm mix() còn nhiều vũ khí bí mật khác nữa. Thay vì truyền vào 1 số thực float để chỉ định tỉ lệ trộn 2 màu, bạn có thay nó bằng một vec3 (hoặc vec4 tuỳ vào định dạng của 2 màu gốc) để chỉ định tỉ lệ trộn màu cho từng kênh r, g, b (và cả a) riêng biệt.

Hãy xem đoạn code ví dụ dưới đây. Cũng tương tự như ở chương trước, tôi sẽ vẽ đồ thị của hàm số được dùng để chỉ định tỉ lệ trộn màu. Hiện tại thì tất cả các kênh đều dùng chung 1 hàm số nên sẽ có đồ thị giống nhau.

Bạn hãy thử uncomment dòng số 25 xem điều gì xảy ra. Rồi lần lượt cả dòng 26 và 27 nữa. Bạn sẽ thấy mỗi kênh của 2 màu colorA và colorB lại được trộn với nhau theo một tỉ lệ riêng.

Chắc hẳn bạn chưa quên 3 hàm số tôi dùng ở các dòng từ 25 tới 27 đâu nhỉ. Hãy thí nghiệm thoải mái với chúng đi. Kiến thức từ chương trước sẽ giúp bạn tạo nên rất nhiều dải màu gradient thú vị đó. Hãy thử:

• Tạo dải màu gradient mô phỏng cảnh hoàng hôn của William Turner

• Chuyển qua lại giữa màu bình minh và hoàng hôn bằng cách dùng biến u_time.

• Tạo dải màu 7 sắc cầu vồng

• Sử dụng hàm step() để tạo nên những lá cờ sặc sỡ

HSB

Ta không thể học về màu sắc mà không đề cập tới không gian màu được. Có thể bạn đã biết, chúng ta có nhiều cách khác nhau để lưu trữ màu ngoài cách dùng 3 kênh đỏ, xanh lá, xanh dương.

HSB là viết tắt của Hue (sắc độ), Saturation (độ bão hoà màu) và Brightness (hoặc Value, độ sáng), là một cách định dạng màu khác, vốn có tổ chức và dễ hiểu hơn nhiều. Hãy dành vài phút để đọc hiểu 2 hàm rgb2hsv() và hsv2rgb() trong đoạn code dưới đây.

Bằng cách ánh xạ vị trí trên trục X với Hue, vị trí trên trục Y với Brightness, ta có được dải phổ của những màu sắc có thể quan sát được bằng mắt thường. Cách phân bố màu trên không gian kiểu này của HSB giúp cho việc chọn màu dễ hơn cách dùng RGB nhiều.

HSB trong hệ toạ độ cực

HSB ban đầu được thiết kế để biểu diễn bằng hệ toạ độ cực (vị trí mỗi điểm được xác định bằng khoảng cách tới gốc toạ độ và góc phương vị - góc so với 1 trục toạ độ duy nhất), thay vì hệ toạ độ Đề-các. Giả sử toàn bộ canvas sẽ được dùng để biểu diễn hệ toạ độ cực. Để chuyển đổi màu ở định dạng HSB từ hệ toạ độ Đề-các sang hệ toạ độ cực thì ta cần xác định được khoảng cách từ 1 điểm ảnh trên canvas tới điểm chính giữa của canvas (chính là gốc toạ độ cực), rồi tính góc nghiêng của vector từ tâm tới điểm ảnh đó với trục hoành. Để làm được điều này thì ta cần dùng tới các hàm length() và atan(y,x) (ở các ngôn ngữ shader khác thì người ta hay dùng hàm atan2(y,x) còn trong GLSL thì đó chính là hàm atan này, nhờ có overload).

Khi sử dụng các hàm vector và lượng giác, vec2, vec3 và vec4 sẽ chẳng khác gì vector thông thường, kể cả bạn có dùng nó để biểu diễn màu đi chăng nữa. Vì vậy ta sẽ coi như màu sắc và vector tương đương nhau, thực tế cho thấy lối suy nghĩ linh hoạt này sẽ rất hữu dụng.

Chú ý: Các hàm hình học, ngoài length ra thì còn rất nhiều: distance(), dot(), cross, normalize(), faceforward(), reflect() và refract(). GLSL cũng có nhiều hàm đặc biệt dành riêng cho vector như: lessThan(), lessThanEqual(), greaterThan(), greaterThanEqual(), equal() và notEqual().

Khi ta đã có góc và khoảng cách trong hệ toạ độ cực rồi, ta cần "chuẩn hoá" (normalize) các giá trị đó sao cho chúng nằm trong khoảng [0.0, 1.0]. Ở dòng 27, hàm atan(y,x) sẽ cho kết quả là góc tính bằng đơn vị radian, nằm trong khoảng [-PI, PI] tương đương với [-3.14, 3.14]. Vậy để chuẩn hoá về khoảng [0.0, 1.0], ta sẽ "remap" góc đó bằng cách chia cho 2 PI (dùng hằng số TWO_PI được định nghĩa trên đầu) rồi cộng kết quả thu được với 0.5. Còn với khoảng cách thì dễ rồi, giá trị lớn nhất mà nó có thể đạt được trong canvas là 0.5, cũng chính là bán kính đường tròn ngoại tiếp của canvas. Vậy nên để "remap" khoảng cách về khoảng [0.0, 1.0] thì ta chỉ cần x2.

Và đó cũng chính là phần chủ đạo trong đoạn code dưới đây.

Hãy thử sửa code sao cho:

• Dải màu HSB quay vòng vòng như bánh xe màu.

• Sử dụng các hàm số cơ bản kết hợp với các hàm chuyển đổi định dạng HSB sang RGB để co giãn 1 dải Hue nhất định nào đó.

• Nếu quan sát kỹ bánh xe màu được dùng để chọn màu (như hình dưới), bạn sẽ thấy các dải phổ của nó hơi khác một chút vì nó dùng không gian màu RYB. Ví dụ, màu ở vị trí đối diện với đỏ trên bánh xe là màu xanh lá, còn ở ví dụ trên thì ta lại thấy đó là màu xanh da trời (cyan). Bạn có thể sửa code để tạo ra bánh xe màu giống như hình này không? (Gợi ý: hàm số)

• Hãy đọc quyển 'Interaction of Color' của Josef Albers và dùng các shader dưới đây để thực hành.

Chú ý về hàm và tham số

Trước khi sang chương tiếp theo hãy cùng nhìn lại một chút bằng cách quan sát các hàm số đã dùng. Bạn sẽ thấy có từ khoá in được đặt trước kiểu dữ liệu của mỗi tham số. Từ khoá này là một trong những qualifier của GLSL và trong trường hợp này thì nó cho ta / GPU biết rằng mọi thay đổi trong hàm này sẽ không làm thay đổi giá trị của biến bên ngoài được truyền vào làm tham số. Ta sẽ còn thấy thêm các qualifier khác ở các chương tiếp theo như out và inout. Qualifier inout, đại khái là sẽ khiến cho biến đó được truyền vào hàm với dạng tham chiếu (reference), nên mọi thay đổi trong hàm này đối với biến đó sẽ được giữ nguyên khi ra khỏi hàm.

int newFunction(in vec4 aVec4,      // read-only
                out vec3 aVec3,     // write-only
                inout int aInt);    // read-write

Ở chương tiếp theo ta sẽ dùng tất cả kiến thức đã học được trước đó để tạo nên các hình khối bằng cách pha trộn (blend) các không gian lại với nhau. Bạn không đọc nhầm đâu, ... pha trộn các không gian đó.