Kształty

Nareszcie! Czekaliśmy na ten moment! Poznałeś większość podstaw GLSL, jego typów i funkcji. Ćwiczyłeś również wykorzystanie shaping functions. Teraz nadszedł czas, aby połączyć to wszystko w całość. Jesteś w stanie sprostać temu wyzwaniu! W tym rozdziale dowiesz się, jak procedrualnie i równolegle rysować proste kształty.

Prostokąt

Wyobraźmy sobie, że mamy papier w kratkę, taki jaki używaliśmy na lekcjach matematyki i naszym zadaniem domowym jest narysowanie kwadratu. Kartka papieru jest w wymiarach 10x10, a kwadrat w 8x8. Co zrobisz?

Zamalowałbyś wszystko poza pierwszym i ostatnim rzędem oraz pierwszą i ostatnią kolumną, tak?

Jak to się ma do shaderów? Każdy mały kwadracik naszej kartki papieru to wątek (piksel). Każdy mały kwadrat zna swoje położenie, podobne do współrzędnych na szachownicy. W poprzednich rozdziałach zmapowaliśmy x i y na kanały kolorów czerwony i zielony oraz nauczyliśmy się korzystać z ciasnego dwuwymiarowego terytorium pomiędzy 0.0 a 1.0. Jak możemy tę wiedzę wykorzystać, aby narysować wyśrodkowany kwadrat na środku naszej kanwy?

Zacznijmy od naszkicowania pseudokodu, który używa ifów na współrzędnych kanwy. Idea jest podobna jak w przypadku z papieram w kratke.

if ( (X WIĘKSZE NIŻ 1) ORAZ (Y WIĘKSZE NIŻ 1) )
    pomaluj na biało
else
    pomaluj na czarno

Teraz, gdy mamy lepsze wyobrażenie o tym, jak to będzie działać, zastąpimy ifa funkcją step(), a zamiast używać siatki 10x10 użyjmy znormalizowanych odpowiedników pomiędzy 0.0 a 1.0:

uniform vec2 u_resolution;

void main(){
    vec2 st = gl_FragCoord.xy/u_resolution.xy;
    vec3 color = vec3(0.0);

    // Obie linijki zwracają 1.0 (biały) lub 0.0 (czarny).
    float left = step(0.1,st.x);   // Równoważnie: (X WIĘKSZE NIŻ 0.1)
    float bottom = step(0.1,st.y); // Równoważnie: (Y WIĘKSZE NIŻ 0.1)

    // Mnożenie left*bottom jest podobne do logicznego AND.
    color = vec3( left * bottom );

    gl_FragColor = vec4(color,1.0);
}

Funkcja step() "pomaluje" każdy piksel poniżej 0.1 na czarno (vec3(0.0)) a resztę na biało (vec3(1.0)). Mnożenie pomiędzy left i bottom działa jak logiczna operacja AND, gdzie obie muszą być 1.0 aby zwrócić 1.0, a gdy przynajmniej jedna jest 0.0, to obie są 0.0. W efekcie otrzymujemy dwie czarne linie, jedną na dole, a drugą po lewej stronie kanwy.

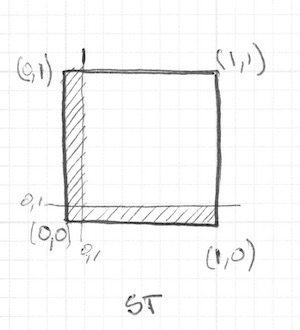
W poprzednim kodzie powtarzamy funkcję step() dla każdej osi (lewej i dolnej). Możemy zaoszczędzić kilka linii kodu, przekazując obie wartości razem zamiast pojedynczo. Wygląda to następująco:

vec2 borders = step(vec2(0.1),st);
float pct = borders.x * borders.y;

Do tej pory narysowaliśmy tylko dwie krawędzie (dolna-lewa) naszego prostokąta. Dorysujmy teraz dwie pozostałe (górna-prawa). Sprawdź następujący kod:

Odkomentuj linijki 21-22 i zobacz jak odwracamy współrzędne st - w ten sposób vec2(0,0,0) znajdzie się w prawym górnym rogu. Otrzymaliśmy odbicie lustrzane. Teraz wystarczy przekazać te odwrócone współrzędne do step().

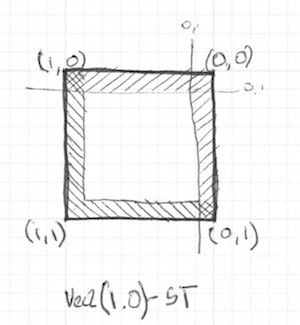
Zwróć uwagę, że w linijkach 18 i 22 wszystkie boki są mnożone przez siebie. Jest to równoznaczne z napisaniem:

vec2 bl = step(vec2(0.1),st);       // bottom-left
vec2 tr = step(vec2(0.1),1.0-st);   // top-right
color = vec3(bl.x * bl.y * tr.x * tr.y);

Ciekawe, prawda? W tej technice chodzi o wykorzystanie step(), odwracania (ang. "flip") współrzędnych oraz mnożenia (jako operację logiczną AND).

Zanim przejdziesz dalej, spróbuj wykonać następujące ćwiczenia:

• Zmień rozmiar i proporcje prostokąta.

• Użyj smoothstep() zamiast step(). Zauważ, że zmieniając wartości, możesz przejść od rozmytych krawędzi do eleganckich gładkich granic.

• Zaimplementuj to samo, ale za pomocą floor() (+ mnożenie i dzielenie).

• Wybierz implementację, którą najbardziej lubisz i zrób z niej funkcję, którą możesz ponownie wykorzystać w przyszłości. Spraw, aby twoja funkcja była elastyczna i wydajna.

• Zrób inną funkcję, która po prostu rysuje kontur prostokąta.

• Jak myślisz, jak można narysować różne prostokąty na tej samej kanwie? Jeśli wymyślisz jak, pochwal się swoimi umiejętnościami, tworząc kompozycję z prostokątów i kolorów, która przypomina obraz Pieta Mondriana.

Koła

Łatwo jest rysować kwadraty na papierze w kratkę i prostokąty na współrzędnych kartezjańskich, ale okręgi wymagają innego podejścia, zwłaszcza że potrzebujemy algorytmu działającego na każdym pikselu z osobna. Jednym z rozwiązań jest zmapowanie współrzędnych tak, abyśmy mogli użyć funkcji step() do narysowania okręgu.

Jak to zrobić? Przypomnijmy sobie lekcje matematyki, gdzie rozpościeraliśmy ramiona cyrkla na długość promienia okręgu, wciskaliśmy jedno ramię cyrkla w środek okręgu, a następnie obrysowywaliśmy krawędź okręgu obracając drugie ramię.

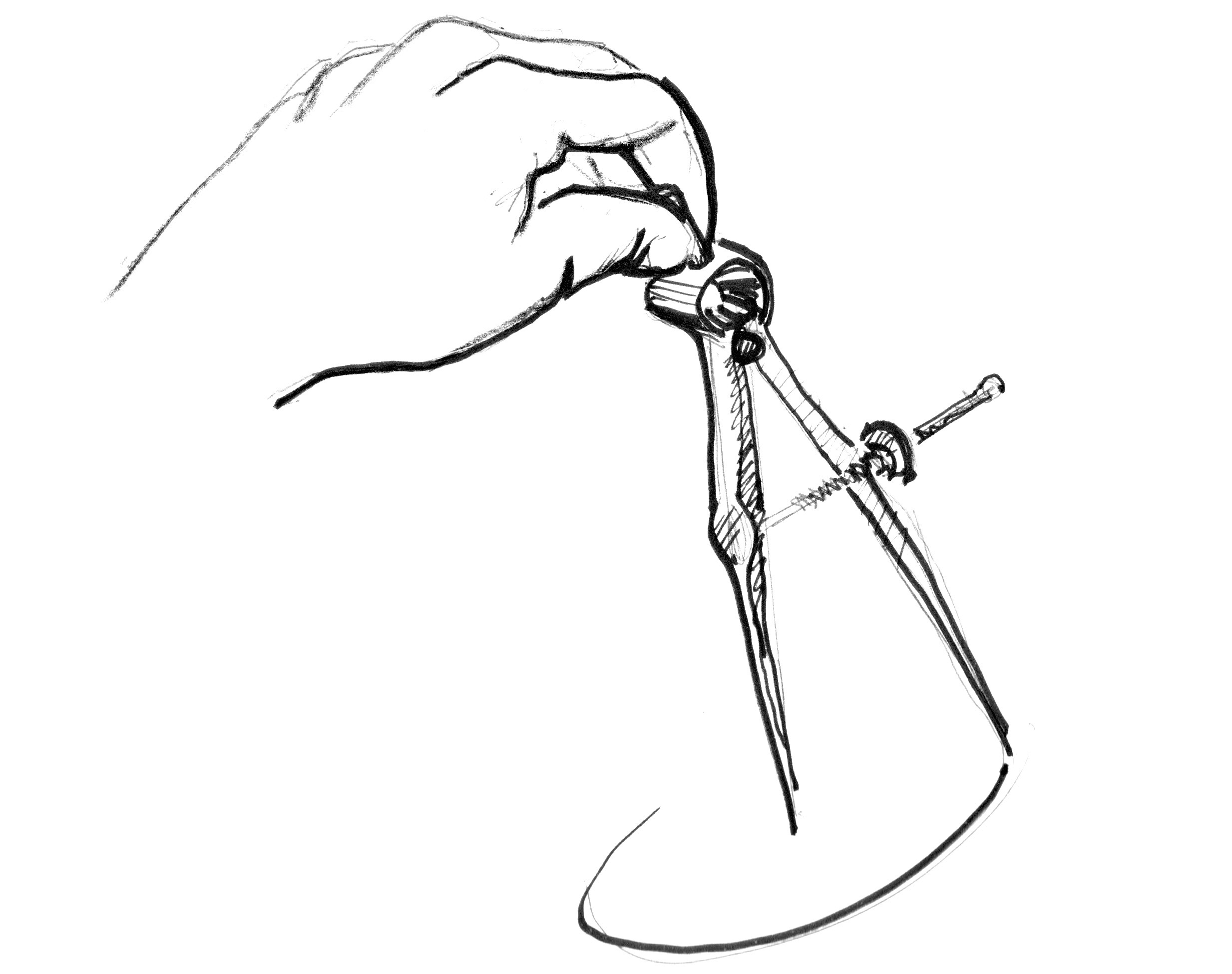
Przełożenie tego na shader, w którym każdy piksel jast jak kratka na papierze, implikuje zadawanie każdemu pikselowi (wątkowi) pytania, czy znajduje się wewnątrz obszaru koła. Robimy to poprzez obliczenie odległości od danego piksela do środka okręgu.

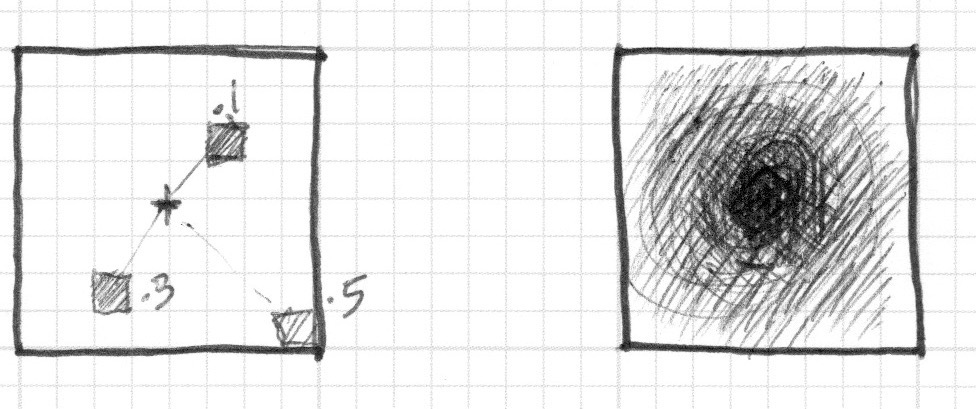
Istnieje kilka sposobów na obliczenie tej odległości. Najprostszy z nich wykorzystuje funkcję distance(), która oblicza length() różnicy pomiędzy dwoma punktami (w naszym przypadku współrzędną piksela i środkiem kanwy). Funkcja length() to nic innego jak przekształcone twierdzenie Pitagorasa:

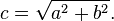
Możesz użyć distance(), length() lub sqrt() aby obliczyć odległość do centrum kanwy. Poniższy kod zawiera te trzy funkcje i nie zaskakuje fakt, że każda z nich zwraca dokładnie taki sam wynik.

Zakomentuj i odkomentuj linijki, aby wypróbować różne sposoby uzyskania tego samego wyniku.

W powyższym przykładzie mapujemy odległość do centrum kanwy na jasność piksela. Im bliżej centrum znajduje się piksel, tym niższą (ciemniejszą) ma wartość. Zauważ, że wartości nie są zbyt wysokie, ponieważ od centrum ( vec2(0.5, 0.5) ) maksymalna odległość ledwo przekracza 0.5. Pokontempluj nad dokonanym mapowaniem i pomyśl:

• Co można z niego wywnioskować?

• Jak możemy je użyć do narysowania koła?

• Zmodyfikuj powyższy kod, aby zawrzeć cały gradient wewnątrz kanwy. (Wskazówka: użyj mnożenia)

Pole odległości

Możemy również myśleć o powyższym przykładzie jako o mapie wysokości, gdzie im ciemniej tym wyżej. Gradient pokazuje nam coś podobnego do wzoru tworzonego przez stożek. Wyobraź sobie, że jesteś na szczycie tego stożka. Pozioma odległość do krawędzi stożka wynosi 0.5. Będzie ona stała we wszystkich kierunkach. Wybierając miejsce "przecięcia" stożka otrzymamy większą lub mniejszą powierzchnię kołową.

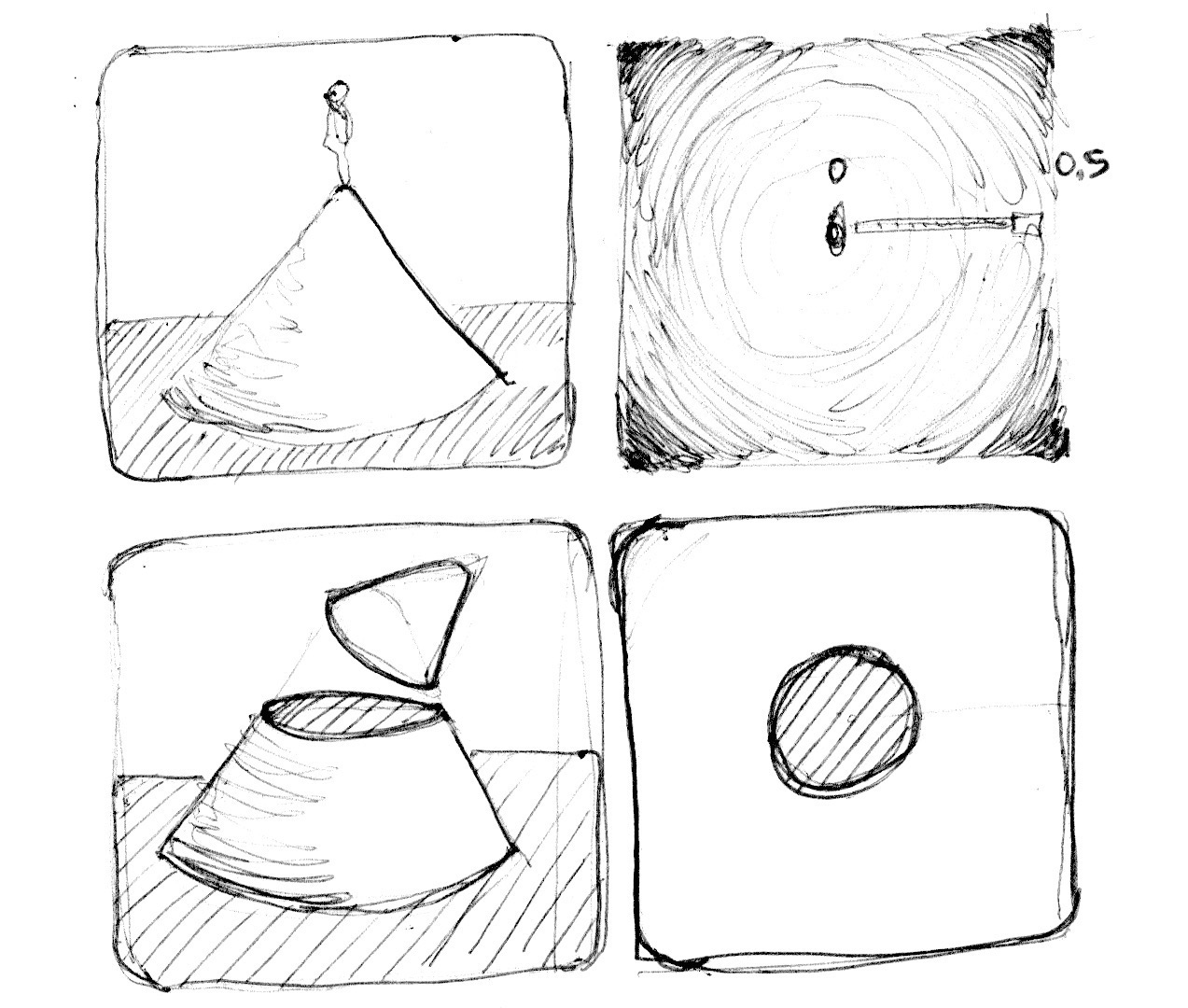
Zasadniczo używamy reinterpretacji przestrzeni (w oparciu o odległość do centrum), aby tworzyć kształty. Ta technika jest znana jako "pole odległości" (ang "distance field") i jest używana na różne sposoby, od konturów czcionek do grafiki 3D.

Spróbuj następujących ćwiczeń:

• Użyj step(), aby zamienić wszystko powyżej 0.5 na białe, a wszystko poniżej na czarne.

• Odwróć kolory tła i pierwszego planu.

• Używając smoothstep(), poeksperymentuj z różnymi wartościami, aby uzyskać ładne, gładkie granice na swoim okręgu.

• Gdy już będziesz zadowolony ze swojej implementacji, stwórz z niej funkcję, którą będziesz mógł ponownie wykorzystać w przyszłości.

• Dodaj kolor do koła.

• Czy możesz zanimować swój krąg, aby rosnął i kurczył się, symulując bijące serce? (Możesz zaczerpnąć inspirację z animacji w poprzednim rozdziale).

• A co z przesuwaniem tego okręgu? Czy możesz go przesuwać i umieszczać różne okręgi na jednej kanwie?

• Co się stanie, jeśli połączysz pola odległości razem, używając różnych funkcji i operacji?

pct = distance(st,vec2(0.4)) + distance(st,vec2(0.6));
pct = distance(st,vec2(0.4)) * distance(st,vec2(0.6));
pct = min(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = max(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = pow(distance(st,vec2(0.4)),distance(st,vec2(0.6)));

• Zrób trzy kompozycje z wykorzystaniem tej techniki. Jeśli są one animowane, jeszcze lepiej!

Twoja skrzynka z narzędziami

Pod względem mocy obliczeniowej funkcja sqrt() - i wszystkie funkcje, które od niej zależą - mogą być kosztowne. Oto inny sposób tworzenia okrągłego pola odległości za pomocą produktu skalarnego dot():

Przydatne własności pól odległości

Pola odległości mogą być używane do rysowania prawie wszystkiego. Oczywiście im bardziej złożony jest kształt, tym bardziej skomplikowane będzie jego równanie, ale gdy już masz formułę do tworzenia pól odległości danego kształtu, bardzo łatwo jest połączyć i/lub zastosować do niego efekty, takie jak gładkie krawędzie i wiele konturów. Z tego powodu, pola odległości są popularne w renderowaniu czcionek, takich jak Mapbox GL Labels, Matt DesLauriers Material Design Fonts i jak to jest opisane w rozdziale 7 iPhone 3D Programming, O'Reilly.

Przyjrzyj się następującemu kodowi.

Zaczynamy od przeniesienia układu współrzędnych na środek i skurczenia go o połowę, mapując wartości pozycji pomiędzy -1 a 1. W linijce 24 wizualizujemy wartości pola odległości za pomocą funkcji fract() ułatwiając dostrzeżenie tworzonego przez nie wzoru. Wzór pola odległości powtarza się jak pierścienie w ogrodzie Zen.

Przyjrzyjmy się wzorowi pola odległości w linijce 19. Obliczamy tam odległość do współrzędnej (.3,.3) lub vec3(.3) we wszystkich czterech kwadrantach (właśnie po to jest tam abs()).

Jeśli odkomentujesz linijkę 20, zauważysz, że łączymy odległości do tych czterech punktów za pomocą min() do zera. W rezultacie otrzymujemy nowy interesujący wzór.

Spróbuj teraz odkomentować linijkę 21; robimy to samo, ale używamy funkcji max(). Rezultatem jest prostokąt z zaokrąglonymi rogami. Zauważ, jak pierścienie pola odległości stają się gładsze, im bardziej oddalają się od środka.

Dokończ odkomentowywanie linijek 27 do 29 jedna po drugiej, aby zrozumieć różne zastosowania pól odległości.

Krzywe biegunowe

W rozdziale o kolorze mapujemy współrzędne kartezjańskie na współrzędne biegunowe, obliczając promień i kąt każdego piksela za pomocą następującego wzoru:

vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0;
float a = atan(pos.y,pos.x);

Część tego wzoru wykorzystaliśmy na początku rozdziału do narysowania okręgu. Odległość do środka obliczyliśmy za pomocą length(). Teraz, gdy wiemy już o polach odległości, możemy poznać inny sposób rysowania kształtów za pomocą współrzędnych biegunowych.

Technika ta jest nieco restrykcyjna, ale bardzo prosta. Polega ona na zmianie promienia okręgu w zależności od kąta, aby uzyskać różne kształty. Jak dokonuje się ta zmiana? Z użyciem shaping functions!

Poniżej znajdziesz dwa interaktywne przykłady, w których te same funkcje występują we współrzędnych kartezjańskich i w biegunowych (pomiędzy linijkami 21 i 25). Odkomentuj te funkcje jedna za drugą, zwracając uwagę na zależności między jednym układem współrzędnych a drugim.

Spróbuj:

• Zanimować te kształty
• Połącz różne shaping functions by zrobić dziury w kształtach, aby powstały kwiaty, płatki śniegu i zębatki.
• Użyj funkcji plot() z rodziału Shaping functions i narysuj sam kontur (bez wypełnienia)

Łącząc siły

Teraz gdy wiemy, jak zmieniać promień koła w zależności od kąta z użyciem atan(), możemy spróbować połączyć atan() z polami odległości.

Trik polega na wykorzystaniu liczby krawędzi wielokąta, by skonstruować pole odległości z użyciem współrzędnych polarnych. Sprawdź następujący kod od Andrew Baldwin.

• Korzystając z tego przykładu, stwórz funkcję, która przyjmuje położenie i liczbę kątów pożądanego wielokąta, a zwraca wartość pola odległości.

• Połącz pola odległości ze sobą z użyciem min() i max().

• Zreplikuj dowolne logo z użyciem pól odległości

Gratulacje! Udało ci się przebrnąć przez bardzo trudny materiał! Choć rysowanie prostych kształtów w Processing jest proste, to tutaj już nie. W świecie shaderów rysowanie kształtów jest zawiłe; przestawienie się na ten nowy sposób programowania może być męczące.

Na dole strony znajdziesz link do PixelSpirit Deck. Jest to talia kart, która pomoże ci nauczyć się nowych funkcji SDF (ang. "Signed distance field" - pole odległości z uwzględnieniem wartości ujemnych), które wykorzystasz w swoich pracach i shaderach. Poziom trudności jest progresywny, więc praca nad jedną kartą dziennie zapewni ci wyzwania na kolejne miesiące.

Wiedząc jak rysować kształty, z pewnością przyjdą ci do głowy nowe pomysły. W następnym rozdziale nauczysz się przesuwać, obracać i skalować kształty. Pozwoli ci to tworzyć kompozycje!