Formas

Finalmente! A gente vem construindo habilidades para este momento! Você aprendeu a maioria das fundações, tipo s funções GLSL. Você praticou suas equações de formas várias vezes. Agora é a hora de juntar tudo. Você está pronto para este desafio! Neste capítulo, vai aprender como desenhar formas simples, de forma procedural paralela.

Retângulo

Imagine que tenhamos um papel quadriculado como os que usamos nas aulas e exercícios de casa de matemática, e queremos desenhar um quadrado. O tamanho do papel é 10x10 e o quadrado deveria ser 8x8. O que você vai fazer?

Você pintaria tudo, menos a primeira linha e a última, e a primeira coluna e a última, certo?

E como isso se relaciona com os shaders? Cada quadradinho de nosso papel é uma thread (um pixel). Cada quadradinho sabe sua posição, como as coordenadas de um tabuleiro de xadrez. Em capítulos anteriores, nós mapeamos x e y para os canais de cores vermelho e verde, e aprendemos como usar o estreito território bidimensional entre 0.0 e 1.0. Como podemos usar isso para desenhar um quadrado centralizado no meio da nossa tela?

Vamos começar rascunhando um pseudocódigo que usa vários if no campo espacial. Os princípios para fazer isso são notavelmente similares ao modo que pensamos no cenário do papel quadriculado.

if ( (X MAIOR QUE 1) AND (Y MAIOR QUE 1) )
    pinta de branco
else
    pinta de preto

Agora que temos uma ideia melhor de como isos vai funcionar, vamos substituir os if com step(), e, em vez de usar 10x10, vamos usar valores normalizados entre 0.0 e 1.0:

uniform vec2 u_resolution;

void main(){
    vec2 st = gl_FragCoord.xy/u_resolution.xy;
    vec3 color = vec3(0.0);

    // Cada resultado retorna  1.0 (branco) ou 0.0 (preto).
    float left = step(0.1,st.x);   // Similar a ( X maior que 0.1 )
    float bottom = step(0.1,st.y); // Similar a ( Y maior que 0.1 )

    // A multiplicação left*bottom vai ser similar ao AND lógico.
    color = vec3( left * bottom );

    gl_FragColor = vec4(color,1.0);
}

A função step() vai tornar cada pixel abaixo de 0.1 preto (vec3(0.0)) e o resto branco (vec3(1.0)) . A multiplicação entre left e bottom funciona como um AND lógico, onde os dois devem estar 1.0 para retornar 1.0. Isso desenha duas linhas pretas, uma no fundo, e outra na lado esquerdo do canvas.

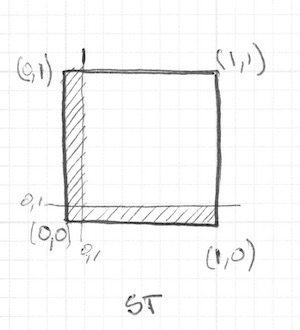
No código anterior, repetimos a estrutura para cada eixo (esquerdo e fundo). Podemos economizar algumas linhas de código, passando 2 vaores diretamente para step() ao invés de apenas um. Seria algo assim:

vec2 borders = step(vec2(0.1),st);
float pct = borders.x * borders.y;

Até agora, só desenhamos duas bordar (fundo-esquerda) de nosso retângulo. Vamos desenhar as outras duas (topo-direita). Veja esse código:

Descomente as linhas 21-22 e veja como invertemos as coordenadas st e repetimos a mesma função step(). Desse jeito, o vec2(0.0,0.0) vai estar no canto superior direito. Isso é o equivalente digital a girar a página e repetir o mesmo procedimento.

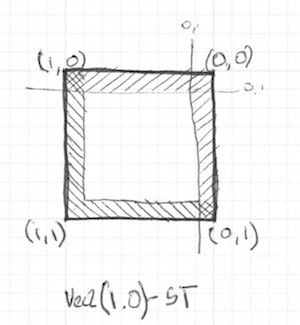
Note que nas linhas 18 e 22, todos os lados estão sendo multiplicados juntos. É o mesmo que escrever:

vec2 bl = step(vec2(0.1),st);       // bottom-left
vec2 tr = step(vec2(0.1),1.0-st);   // top-right
color = vec3(bl.x * bl.y * tr.x * tr.y);

Interessante, certo? Essa técnica é, basicamente, usar step() e multiplicação para operações lógicas, e flipar as coordenadas.

Antes de prosseguir, tente os exercícios a seguir:

• Mude o tamanho e as proporções do retângulo.

• Experimente com o mesmo código, mas usando smoothstep() no lugar de step(). Note que, ao mudar os valores, você pode ir de beiradas embaçadas até elegantes bordas suaves.

• Faça uma outra implementação que use floor().

• Escolha a implementação de que gostar mais, e faça uma função dela, que você possa reutilizar no futuro. Deixe sua função flexível e eficiente.

• Faça outra função que apenas desenhe o contorno do retângulo.

• Como você acha que poderia mover e colocar retângulos diferentes na mesma tela? Se descobrir como, mostre suas habilidades fazendo uma composição de retângulos e cores que se pareça com uma pintura de Piet Mondrian.

Círculos

É fácil desenhar quadrados em um papel quadriculado, e retângulos em coordenadas cartesianas, mas círculos requerem outra abordagem, especialmente porque precisamos de um algoritmo "por pixel". Uma solução é remapear as coordenadas espaciais de modo que possamos usar uma função step() para desenhar um círculo.

Como? Vamos começar, voltando um pouco às aulas de matemática e o papel quadriculado, onde nós abríamos um compasso até o raio do círculo, apertamos uma das pontas do compasso no centro do círculo, e então tracejamos o contorno do círculo com uma rodada do compasso.

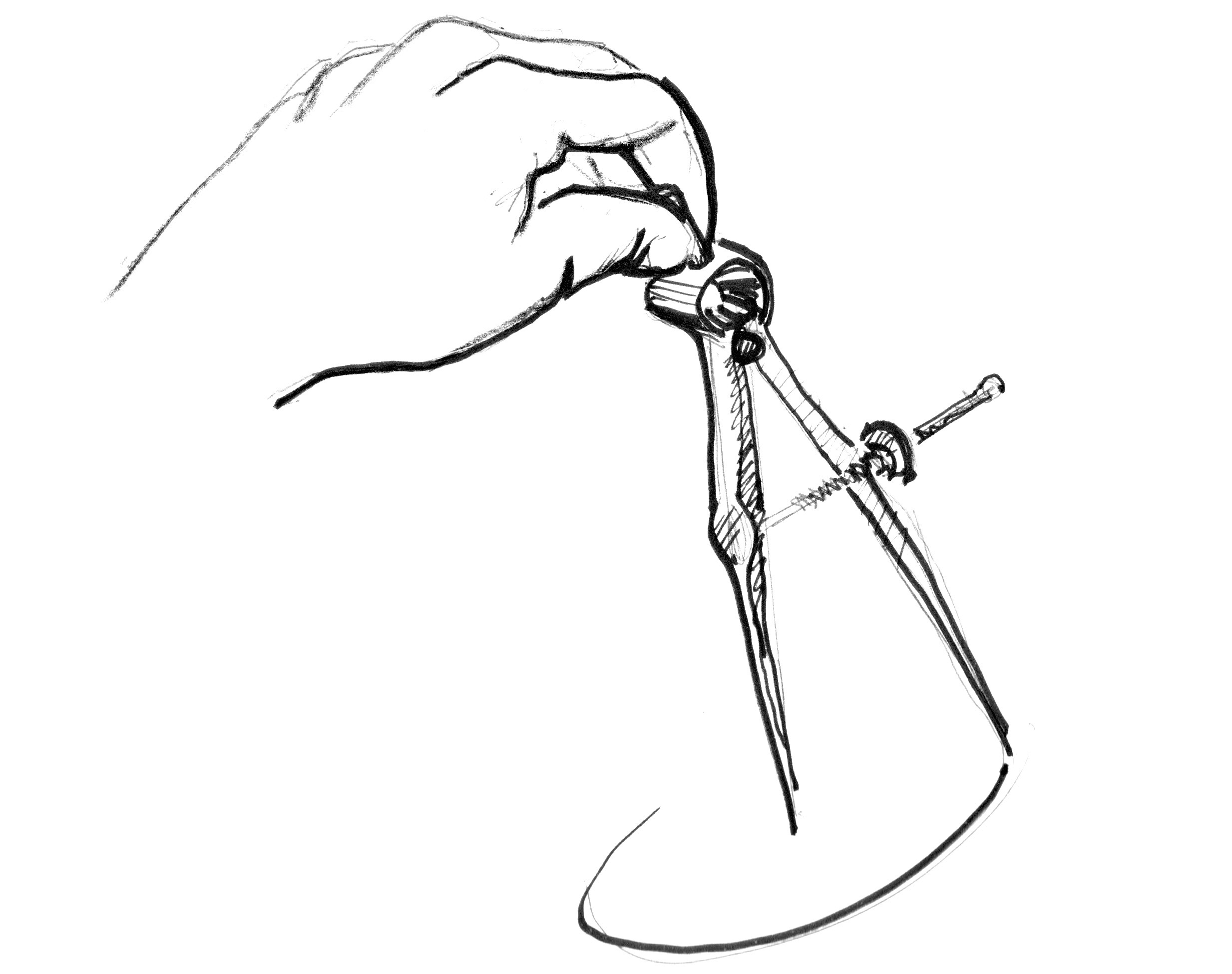
Traduzindo isso para um shader, onde cada quadrado no papel é um pixel, implica em perguntar a cada pixel (ou thread) se ele está dentro da área do círculo. Fazemos isso calculando a distância do pixel até o centro do círculo.

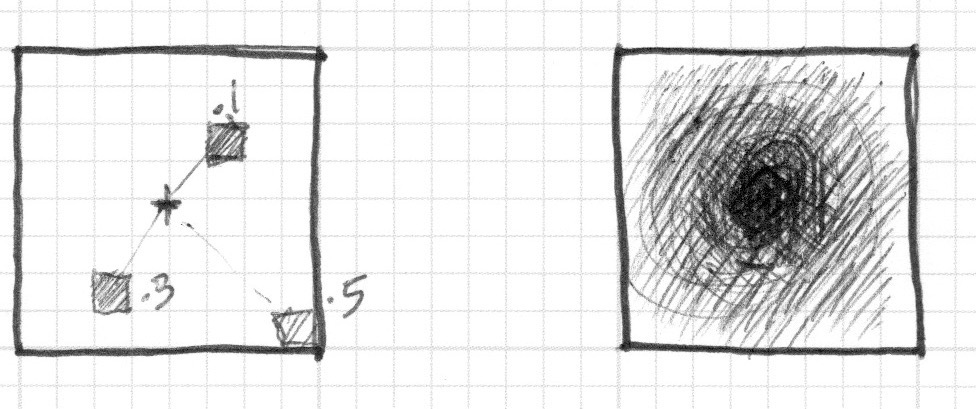
Existem várias formas de se calcular essa distância. A mais fácil usa a função distance(), que, internamente, calcula o length() (comprimento) da diferença entre dois pontos (em nosso caso, a coordenada do pixel, e o centro da tela). A função length() nada mais é que um atalho para a equação de hipotenusa que usa raiz quadrada (sqrt()) internamente.

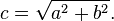
Você pode usar distance(), length() ou sqrt() para calcular a distância até o centro da tela. O código a seguir contém essas três funções e o fato não-surpreendente de que retornam o mesmo resultado.

• Comente e descomente as linhas para testar as diferentes formar de obter o mesmo resultado.

No exemplo anterior, nós mapeamos a distância até o centro para o brilho da cor de cada pixel. Quanto mais ao centro está um pixel, mais escuro ele é (menor valor de cor). Note que os valores não ficam muito altos porque a partir do centro ( vec2(0.5, 0.5) ) a distância máxima mal passa de 0.5. Contemple esse mapa e pense:

• O que você pode inferir disso?

• Como podemos usar isso para desen um círculo?

• Modifique o código acima, de modo a conter o gradiente circular inteiro dentro do canvas.

Campo de distância

Também podemos pensar no exemplo acima como um mapa de altitude, onde áreas mais escuras implicam em maior altura. O gradiente nos mostra algo similar ao padrão feito por um cone. Imagine-se no topo desse cone. A distância horizontal até a borda do cone é 0.5. Isso será constante em todas as direções. Escolhendo onde "cortar" o cone, vai te dar uma superfície circular maior ou menor.

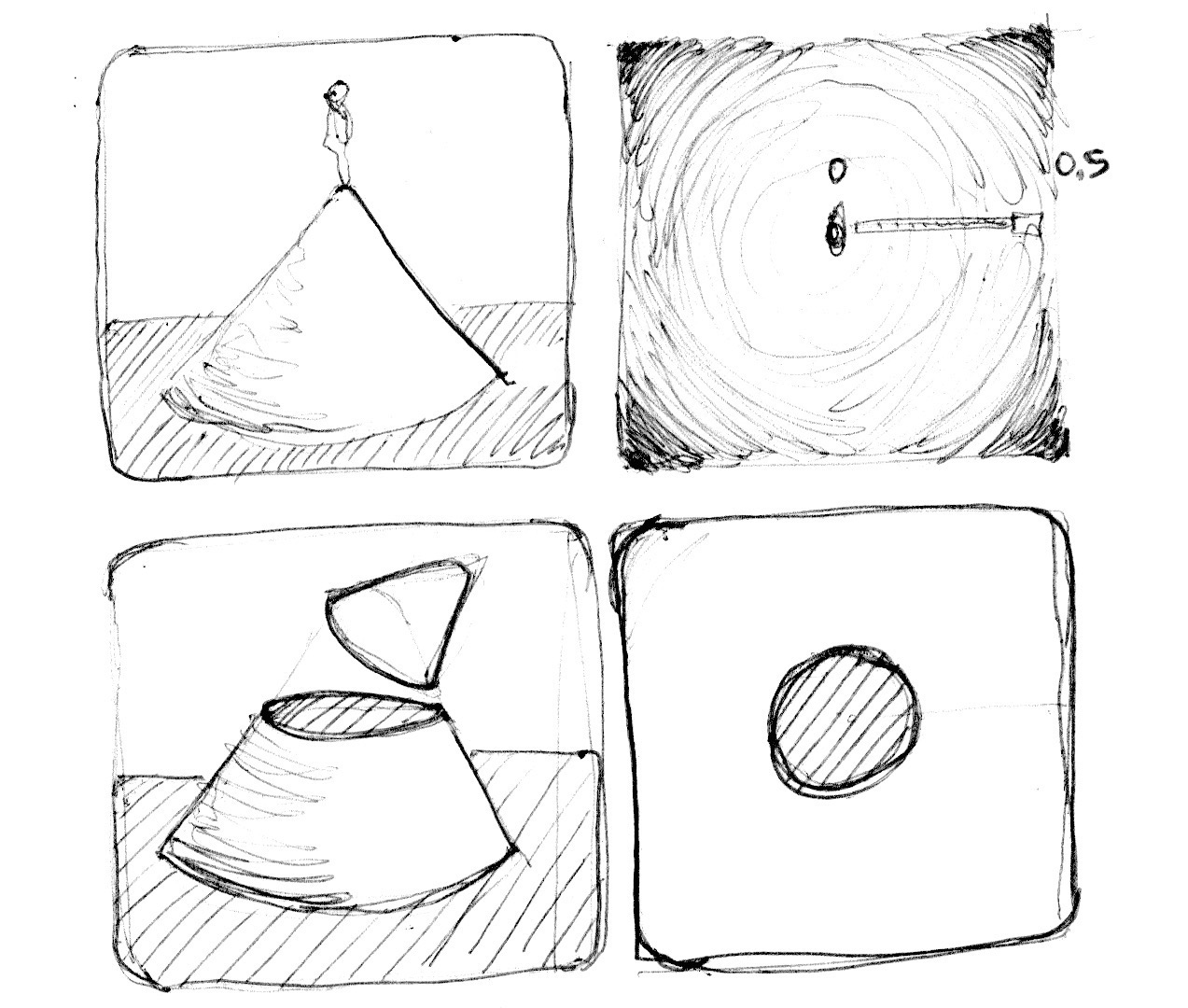
Basicamente, estamos usando uma reinterpretação do espaço (baseado na distância até o centro) para fazer formas. Essa técnica é conhecida como "campo de distância" e é usada e diferentes modos, desde outlines de fontes até gráficos 3D.

Tente os seguintes exercícios:

• Use o step() para tornar tudo acima de 0.5 em branco e tudo abaixo para 0.0.

• Inverta as cores do fundo e do primeiro plano.

• Usando smoothstep(), faça experiências com valores diferentes para conseguir uma borda suave no seu círculo.

• Uma vez que esteja feliz com uma implementação, faça uma função com ela, para reutilizar no futuro.

• Adicione cor ao círculo.

• Você pode animar seu círculo, para crescer e encolher, simulando a batida de um coração? (Você pode ter alguma inspiração, da animação do capítulo anterior)

• Que tal mover esse círculo? Você consegue movê-lo para lugares diferentes na tela?

• O que acontece se você combinar campos de distância usando diferentes funções e operações?

pct = distance(st,vec2(0.4)) + distance(st,vec2(0.6));
pct = distance(st,vec2(0.4)) * distance(st,vec2(0.6));
pct = min(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = max(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = pow(distance(st,vec2(0.4)),distance(st,vec2(0.6)));

• Faça três composições usando essa técnica. Se forem animadas, melhor ainda!

Para sua caixa de ferramentas

Em termos de poder computacional, a função sqrt() - e todas as que dependem dela - pode ser bem cara. Aqui vai outra forma de criar um campo de distância usando dot() (produto escalar).

Propriedades úteis de um Campo de Distância

Campos de Distância podem ser usados para desenhar quase tudo. Obviamente, quanto mais complexa for uma forma, mais complicada vai ser a equação, mas uma vez que você tenha a fórmula para fazer um campo de distância de uma forma específica, é muito fácil combinar e/ou aplicar efeitos a ela, como bordas suaves, e múltiplos outlines. Por causa disso, os campos de distância são populares para rendereizar fontes, como Mapbox GL Labels, Matt DesLauriers Material Design Fonts e como descrito no capítulo 7 do livro iPhone 3D Programming, O’Reilly.

Dê uma olhada no código a seguir.

Começamos movendo o sistema de coordenadas para o centro e encolhendo-o pela metade, para remapear os valores de posição entre -1 e 1. Também, na linha 24, estamos visualizando os valores do campo de distância usando uma função fract() para facilitar que você veja o padrão que eles criam. O padrão do campo de distância se repete o tempo todo, como anéis num jardim Zen.

Vamos dar uma olhada na fórmula do campo, na linha 19. Ali, estamos calculando a distância até a posição (.3,.3) ou vec3(.3) em todos os nossos quatro quadrantes (é isso o que o abs() está fazendo aqui).

Se você descomentar a linha 20, vai notar que estamos combinando as distâncias para esses quatro pontos usando o min() para zero. O resultado produz um novo padrão bem interessante.

Agora, tente descomentar a linha 21; estamos fazendo o mesmo, mas usando a função max(). O rsultado é um retângulo com cantos arredondados. Note como os anéis do cmapo ditância ficam mais suaves quanto mais disntantes do centro.

Termine de descomentar as linhas 27 a 29 uma a uma, para entender os diferentes usos de um padrão de campo de distância.

Formas Polares

No capítulo sobre sores, nós mapeamos as coordenadas cartesianas para coordenadas polares, calculando o raio e os ângulos de cada pixel com essa fórmula:

vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0;
float a = atan(pos.y,pos.x);

Usamos parte desta fórmula no começo do capítulo para desenhar um círculo. Nós calculamos a distância até o centro usando length(). Agora que sabemos sobre os os campos de distância, podemos aprender outra forma de desenhar formar, usando coordenadas polares.

Esta técnica é um pouco restritiva, mas bem simples. Ela consiste em mudar o raio de um círculo dependendo do ângulo, para obter formas diferentes. Como a modulação funciona? Sim, usando funções de formas!

Abaixo, você vai encontrar as mesmas funções do gráfico cartesiano e em um exemplo shader de coordenadas polares (entre as linhas 21 e 25). Descomente as funções uma a uma, prestando atenção na relação entre um sistema de coordenadas e o outro.

Tente:

• Animar essas formas.
• Combinar funções de formas diferentes para cortar buracos na forma, para fazer flores, flocos de neve e engrenagens.
• Use a função plot() que usamos no capítulo sobre Funções de Formas para desenhar só o contorno.

Combinando forças

Agora que aprendemos como modular o raio de um círculo de acordo com o ângulo, usando atan() para desenhar formas diferentes, podemos aprender a usar atan() com campos de distância e aplicar todos os truques e efeitos possíveis com campos de distância.

O truque vai usar o número de lados de um polígono para construir o campo de distância, usando coordenadas polares. Veja o seguinte código do Andrew Baldwin.

• Usando este exemplo, faça uma função que tem como entrada a posição e o número de lados de uma forma desejada, e retorna um valor de campo de distância.

• Misture campos de distância usando min() e max().

• Escolha um logo geométrico para replicar, usando campos de distância.

Parabéns! Você já passou pela parte mais dura! Dê uma pausa e deixe os conceitos assentarem - desenhar formas simples no Processing é fácil, mas não aqui. Na terra dos shaders, desenhar formas é difícil, e pode ser cansativo se adaptar a esse novo paradigma de programação.

Agora que você já sabe como desenhar formas, tenho certeza de que novas ideias vão pular na sua mente. No capítulo a seguir, você vai aprender como mover, rotacionar e mudar a escala das formas. Isso vai te permitir a fazer composições!