Hình dáng

Cuối cùng thì cũng tới phần này! Ta đã trang bị biết bao kiến thức chỉ để chờ giây phút này thôi đấy! Hầu hết những kiến thức nền tảng của GLSL đều đã được giới thiệu ở các chương trước. Giờ là lúc để kết hợp tất cả những kiến thức đó lại. Ở chương này ta sẽ học cách vẽ những hình khối cơ bản nhất, bằng code, chạy song song trên các bộ vi xử lý của GPU.

Hình chữ nhật

Cứ tưởng tượng rằng ta có một tờ giấy kẻ ô sẵn vẫn hay dùng trong môn Toán và ta phải làm bài tập về nhà là vẽ một hình vuông lên đó. Kích thước của tờ giấy là 10x10 còn hình vuông sẽ cỡ 8x8. Làm thế nào nhỉ ?

Bạn sẽ tô màu tất cả các ô của tờ giấy trừ những ô ở dòng trên cùng và dưới cùng, và cả cột đầu tiên lẫn cột cuối cùng nữa, phải không ?

Điều này thì có liên quan gì tới shader ? Mỗi ô vuông nhỏ trên tờ giấy đó có thể coi như một điểm ảnh hay một thread. Ta biết vị trí của từng ô vuông đó, giống như bàn cờ vua ấy mà. Ở các chương trước ta đã ánh xạ toạ độ x và y vào các kênh màu đỏ và xanh lá, và ta cũng đã biết cách để đưa các toạ độ đó về trong khoảng [0.0, 1.0] mà vẫn giữ nguyên tỉ lệ. Áp dụng những điều đó như thế nào để vẽ được hình vuông ở chính giữa canvas bây giờ ?

Hãy bắt đầu bằng đoạn code giả dưới đây có sử dụng lệnh if để kiểm tra từng ô một. Cách làm này cũng giống hệt như cách mà ta chọn các ô sẽ tô màu trên giấy.

if ( (X > 1) AND (Y > 1) )
    tô màu trắng
else
    tô màu đen

Nhưng ta biết có một cách khác, tốt hơn, đó là dùng hàm step(), và thay vì dùng kích thước 10x10 thì ta sẽ dùng các toạ độ đã được chuẩn hoá trong khoảng [0.0, 1.0]

uniform vec2 u_resolution;

void main(){
    vec2 st = gl_FragCoord.xy/u_resolution.xy;
    vec3 color = vec3(0.0);

    // Mỗi dòng dưới đây sẽ cho kết quả 1.0 hoặc 0.0
    float left = step(0.1,st.x);   // Tương đương với ( X > 0.1 )
    float bottom = step(0.1,st.y); // Tương đương với ( Y > 0.1 )

    // Phép nhân left*bottom tương đương với điều kiện logic AND
    color = vec3( left * bottom );

    gl_FragColor = vec4(color,1.0);
}

Hàm step() sẽ chọn màu đen (vec3(0.0)) cho tất cả các điểm ảnh có toạ độ dưới 0.1, và màu trắng (vec3(1.0)) cho tất cả các điểm ảnh còn lại. Phép nhân giữa left và bottom cũng tương đương với lệnh điều kiện logic AND tức là cả 2 giá trị phải bằng 1.0 thì kết quả của phép nhân mới bằng 1.0 được, các trường hợp khác đều cho kết quả 0.0. Đoạn code phía trên sẽ vẽ 2 đường thẳng màu đen, một đường ở phía dưới cùng của canvas, và đường còn lại nằm ở mép trái của canvas.

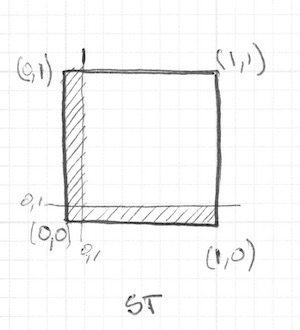
Trong đoạn code phía trên, ta phải sử dụng hàm step() hai lần, mỗi lần cho một trục. Để rút gọn hơn, ta có thể truyền cả 2 toạ độ vào hàm đó cùng lúc như sau:

vec2 borders = step(vec2(0.1),st);
float pct = borders.x * borders.y;

Cho tới lúc này, ta mới chỉ vẽ được 2 đường viền ở dưới cùng và bên trái của hình vuông. Hãy vẽ nốt 2 đường viền còn lại ở phía trên và bên phải nào:

Hãy uncomment dòng 21-22, bạn sẽ thấy tôi đã đảo ngược giá trị của toạ độ st rồi áp dụng y nguyên hàm step() như code cũ. Bằng phép đảo ngược này thì điểm vec2(0.0,0.0) sẽ đại diện cho góc trên cùng bên phải. Hay nói cách khác, tôi đã sử dụng phép chiếu đối xứng.

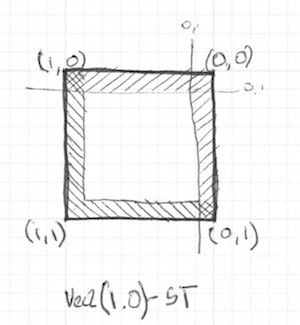
Chú ý: Ở dòng 18 và 22 tất cả kết quả thu được từ 2 hàm step() được nhân với nhau. Đoạn code dưới đây cũng sẽ có tác dụng tương tự:

vec2 bl = step(vec2(0.1),st);       //  Tô màu các ô ở đường viền dưới cùng và bên trái
vec2 tr = step(vec2(0.1),1.0-st);   //  Tô màu các ô ở đường viền trên cùng và bên phải
color = vec3(bl.x * bl.y * tr.x * tr.y);

Ô hay nhỉ ? Toàn bộ bài này chỉ dùng mỗi hàm step() rồi nhân kết quả lại với nhau, kèm theo phép chiếu đối xứng qua tâm.

Trước khi sang phần tiếp theo, hãy thử:

• Thay đổi kích thước của hình vuông / chữ nhật màu trắng

• Thử dùng hàm smoothstep() thay vì step(). Chú ý là khi thay đổi giá trị, ta sẽ thấy các cạnh của hình chữ nhật sẽ thay đổi từ rõ nét sang mờ dần.

• Thử dùng cách khác để vẽ, ví dụ như hàm floor().

• Chọn một cách vẽ bạn thích nhất và biến nó thành 1 hàm mà bạn có thể sử dụng lại trong tương lai. Cố gắng giữ cho hàm đó thật linh hoạt và hiệu quả nhé.

• Tạo một hàm khác chỉ vẽ mỗi đường viền thôi

• Nghĩ xem làm cách nào để đặt nhiều hình chữ nhật có màu sắc và kích thước khác nhau cùng vào trong một canvas nhé ? Nếu bạn nghĩ được cách rồi thì thử dựng lại bức tranh nổi tiếng của Piet Mondrian nhé.

Hình tròn

Vẽ hình vuông trên tờ giấy kẻ ô sẵn hay vẽ hình chữ nhật trong hệ toạ độ Đề-các rất dễ, nhưng để vẽ hình tròn thì ta phải tìm cách khác, đặc biệt là phải chú ý tới từng điểm ảnh một. Một trong những giải pháp được đưa ra là remap toạ độ không gian về một hệ quy chiếu nào đó dựa trên khoảng cách tới tâm rồi dùng hàm step() để loại bỏ các điểm ảnh nằm quá xa tâm.

Quay lại với môn Toán nào, ta sẽ cần 1 tờ giấy có kẻ ô sẵn và 1 chiếc compa. Chỉ cần xoay 1 vòng compa là ta có ngay 1 đường tròn, giờ thì chỉ việc tô màu bên trong đường tròn là được.

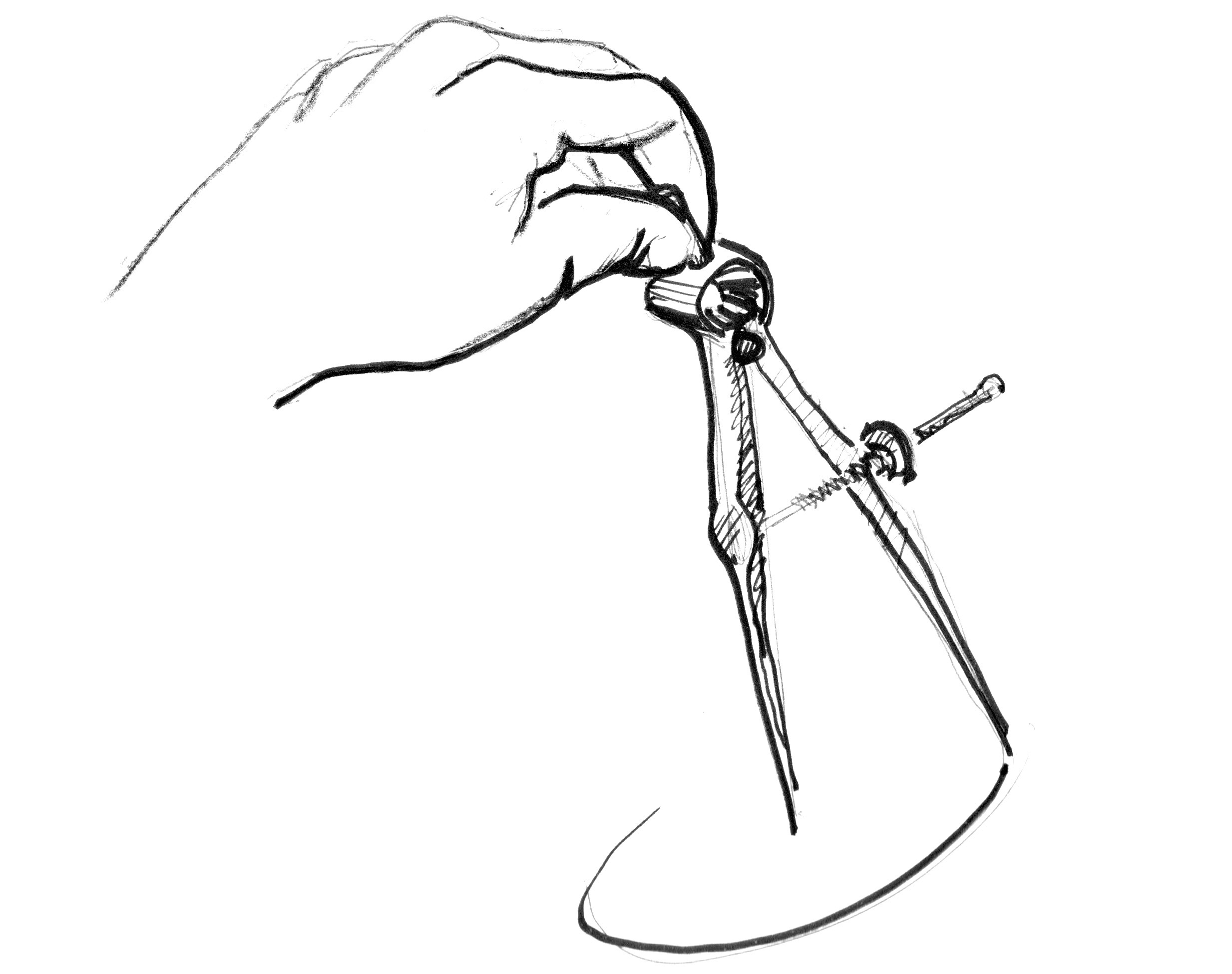
Nếu coi mỗi ô vuông kẻ sẵn trên giấy là 1 điểm ảnh trên canvas, thì để áp dụng cách vẽ tương tự như trên vào trong shader, thực tế ta sẽ phải kiểm tra từng ô một xem nó có nằm bên trong chu vi đường tròn không. Ta có thể biết được điều này bằng cách tính khoảng cách của điểm ảnh đó tới tâm đường tròn.

Có vài cách để tính khoảng cách và cách dễ nhất là dùng hàm distance(), mà bên trong nó sẽ dùng hàm length() để tính độ dài đoạn thẳng nối giữa mỗi điểm ảnh với tâm hình tròn. Để tính độ dài 1 đoạn thẳng, hàm length() sẽ coi đoạn thẳng đó là cạnh huyền của một tam giác rồi áp dụng định lý Pythagores là xong, và công thức đó cần tới hàm căn bậc 2 (sqrt()).

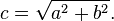
Bạn có thể dùng hàm distance(), length() hay sqrt() tuỳ ý để tính khoảng cách của từng điểm ảnh tới tâm canvas. Đoạn code dưới đây dùng cả 3 hàm trên và không có gì ngạc nhiên là kết quả của chúng đều giống nhau.

• Hãy comment và uncomment từng cách tính để kiểm tra xem có đúng là chúng cho ra cùng 1 kết quả không nhé

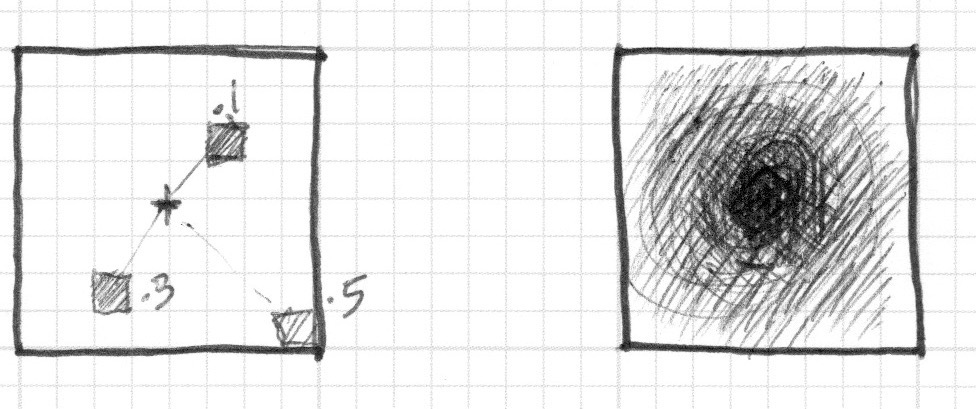
Đoạn code trên minh hoạ khoảng cách từ mỗi điểm ảnh tới tâm canvas bằng màu sắc. Càng gần tâm thì màu càng tối. Ngay cả những điểm xa nhất thì cũng không sáng quá, vì giá trị tối đa chỉ có thể là vec2(0.5, 0.5). Hãy quan sát hình minh hoạ đó và tự hỏi:

• Mình có thể suy luận những gì từ hình này ?

• Làm thế nào để biến nó thành hình tròn ?

• Sửa đoạn code trên để toàn bộ dải màu đen trắng nằm trong canvas thay vì chỉ có nửa tối như hiện tại

Distance field

Nếu coi hình minh hoạ từ ví dụ trên là 1 bản đồ địa hình đo chiều cao, và vùng tối màu là vùng cao hơn, thì ta có thể tưởng tượng ra địa hình đó giống như hình nón. Ở mặt đất thì khoảng cách từ tâm tới mọi điểm khác cùng mặt phẳng đều là 0.5. Vậy nếu ta bổ ngang hình nón tại một độ cao nào đó, thì ta sẽ có 1 lát cắt hình tròn có bán kính tương ứng với độ cao. Càng gần mặt đất thì lát cắt càng lớn. Và ở chiều ngược lại, nếu ta chồng rất nhiều lát cắt hình tròn lên nhau theo thứ tự của bán kính thì ta cũng sẽ thu được 1 hình nón.

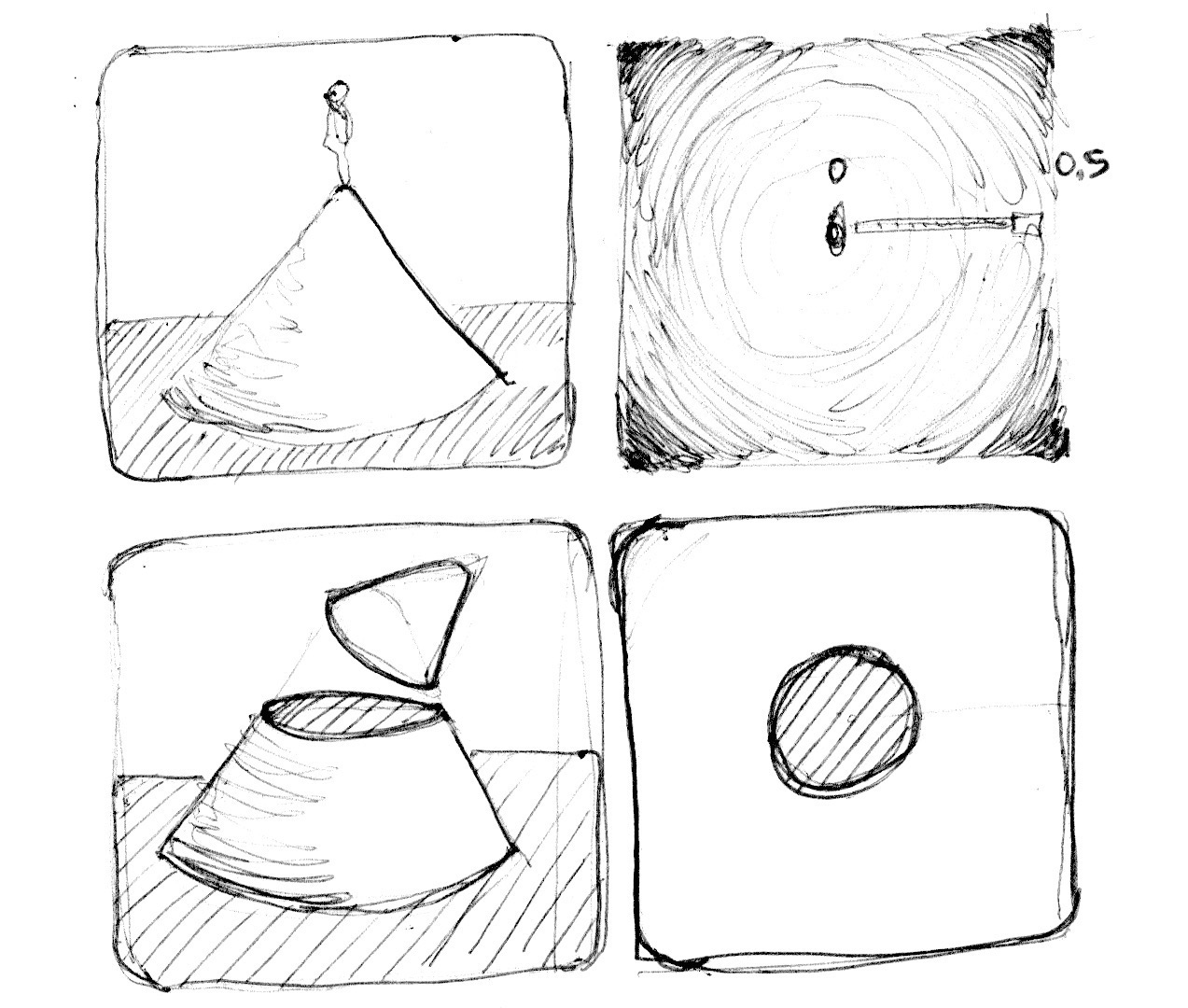
Kỹ thuật này được gọi là "distance field" (trường khoảng cách), và được ứng dụng rất nhiều, từ việc vẽ viền cho các phông chữ cho tới đồ hoạ 3 chiều.

Hãy thử:

• Dùng hàm step() tô màu trắng cho tất cả các điểm xa tâm hơn 0.5 đơn vị, các điểm ảnh còn lại thì màu đen.

• Đảo ngược màu của 2 vùng kể trên.

• Dùng hàm smoothstep(), và điều chỉnh tham số sao cho thu được 1 đường viền có độ mờ mong muốn.

• Biến nó thành 1 hàm mà bạn có thể sử dụng lại trong tương lai. Cố gắng giữ cho hàm đó thật linh hoạt và hiệu quả nhé.

• Tô màu khác cho hình tròn.

• Bạn có thể làm cho hình tròn to ra rồi nhỏ lại theo nhịp tim không ? (Hãy lấy cảm hứng từ chuyển động của chương trước nhé).

• Vậy nếu muốn đặt hình tròn ở các vị trí khác nhau thay vì chỉ ở chính giữa thì sao ?

• Điều gì sẽ xảy ra nếu ta có nhiều hơn 1 distance field và kết hợp chúng lại bằng các hàm toán học cơ bản như dưới đây ?

pct = distance(st,vec2(0.4)) + distance(st,vec2(0.6));
pct = distance(st,vec2(0.4)) * distance(st,vec2(0.6));
pct = min(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = max(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = pow(distance(st,vec2(0.4)),distance(st,vec2(0.6)));

• Hãy tạo ra ba hình cấu tạo từ các phép toán kể trên. Nếu nó chuyển động được thì càng tốt.

Tiện ích

Thực ra thì hàm sqrt() và các hàm gián tiếp sử dụng nó nữa, khá là chậm. Đây là 1 cách khác để tính khoảng cách tới tâm của đường tròn bằng cách tính tích vô hướng của vector dựa vào hàm dot().

Các thuộc tính hữu ích của Distance Field

Các distance field có thể được kết hợp lại với nhau để vẽ hầu như tất cả mọi thứ. Rõ ràng là hình vẽ càng phức tạp thì phương pháp kết hợp chúng sẽ càng rối rắm, nhưng nếu bạn có 1 công thức để tính 1 distance field cho 1 khối hình học cơ bản nào đó rồi, thì việc tạo thêm hiệu ứng cho nó lại rất dễ, uốn cong các cạnh hay vẽ nhiều đường viền cùng lúc chẳng hạn. Chình vì điều này mà distance field là kỹ thuật rất phổ biến khi cần vẽ các ký tự của các phông chữ khác nhau, ví dụ như các phần mềm Mapbox GL Labels, Matt DesLauriers Material Design Fonts và được mô tả chi tiết trong chương 7 của quyển sách iPhone 3D Programming của nhà xuất bản O’Reilly.

Hãy xem đoạn code sau:

Đầu tiên tôi đặt gốc của trục toạ độ ở tâm của canvas rồi remap toạ độ lại để chúng nằm trong khoảng [-1, 1]. Ở dòng 24 tôi có minh hoạ giá trị của các distance field bằng hàm fract() để bạn nhìn rõ tâm của các distance field và tạo nên nhiều đường tròn lồng nhau giống như những cái vòng trên cát trong một khu vườn Thiền vậy.

Hãy nhìn công thức tính distance field ở dòng 19. Tôi tính khoảng cách từ mỗi điểm tới vị trí (.3,.3) viết tắt là vec3(.3), cho mỗi góc phần tư riêng biệt (hàm abs() đã giúp tôi tách riêng 4 góc phần tư ra).

Nếu bạn uncomment dòng 20, bạn sẽ nhận thấy bằng cách dùng hàm min() tôi đã tạo ra hoa văn mới.

Hãy uncomment tiếp dòng 21; tôi dùng hàm max() thay cho hàm min() ở trên. Kết quả là thu được một hình chữ nhật có 4 góc được bo tròn. Hơn thế nữa, càng xa tâm thì 4 góc ngày càng được bo tròn hơn.

Cuối cùng, hãy lần lượt uncomment từng dòng từ 27 tới 29 để thấy các phương pháp vẽ hoa văn khác nhau từ distance field.

Polar shapes - Các hình được tạo ra từ hệ toạ độ cực

Ở chương về màu sắc ta đã chuyển hệ quy chiếu từ hệ toạ độ Đề-các sang hệ toạ độ cực bằng cách tính khoảng cách và góc của mỗi điểm ảnh tới tâm bằng công thức sau:

vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0;
float a = atan(pos.y,pos.x);

Ta cũng đã dùng một phần của công thức này để vẽ hình tròn, cụ thể là dùng hàm length() để tính khoảng cách tới tâm hình tròn. Với kiến thức về distance field, ta có thể áp dụng để vẽ nhiều hình khác trên hệ toạ độ cực.

Kỹ thuật này rất đơn giản, chỉ cần thay đổi khoảng cách tới tâm dựa vào góc nghiêng, là ta sẽ có các hình khác nhau. Nhưng từ góc nghiêng làm thế nào để tính ra khoảng cách mong muốn nhỉ ? Đương nhiên phải dùng hàm số rồi.

Dưới đây là đồ thị của các hàm số được vẽ trên hệ toạ độ Đề-các, còn ở đoạn code sau đó là vẽ trên hệ toạ độ cực (từ dòng 21 tới 25). Hãy uncomment từng hàm số một và chú ý tìm xem mỗi điểm ở hệ toạ độ này nằm ở đâu trong hệ toạ độ kia.

Hãy thử:

• Làm những hình này chuyển động.
• Kết hợp thêm vaì hàm số nữa để đục lỗ những hình trên, có thể sẽ tạo ra hình bông hoa, bông tuyết hay bánh răng.
• Sử dụng hàm plot() từ Chương Các hàm số cơ bản để chỉ vẽ mỗi đường viền thôi thay vì tô màu đặc.

Kết hợp các kiến thức đã học

Ta đã học cách ánh xạ góc nghiêng của hệ toạ độ cực sang khoảng cách để vẽ các hình thú vị, giờ hãy thử áp dụng tất cả những gì đã học với hàm atan() xem sao. Mẹo ở đây là ta sẽ dựng các distance field dựa vào số đỉnh của đa giác. Hãy xem đoạn code này của Andrew Baldwin.

• Dựa vào ví dụ trên đây, hãy tạo một hàm nhận tham số đầu vào là vị trí của tâm và số đỉnh của đa giác để tính distance field nhằm dựng nên đa giác đó.

• Kết hợp các distance field bằng hàm min() và max().

• Vẽ lại một logo hình học nào đó bằng distance field

Xin chúc mừng! Bạn đã vượt qua được phần khó nhằn này rồi ! Hãy tạm nghỉ để suy ngẫm dần các khái niệm này. Vẽ các hình này bằng shader rất thú vị nhưng cũng rất loằng ngoằng.

Đây là URL tới PixelSpirit Deck. Một bộ bài có các biểu tượng được tạo ra bởi các hàm SDF (Signed Distance Field). Bạn hãy thử vẽ lại các biểu tượng đó bằng shader nhé. Các hình vẽ sẽ khó dần lên đấy, thế nên cứ từ từ, mỗi ngày vẽ một hình cũng đủ để mài dũa kỹ năng của bạn về Distance Field ngày càng điêu luyện hơn rồi.

Ở chương tới, chúng ta sẽ học cách di chuyển, quay và thay đổi kích thước của các hình. Từ đó bạn có thể ghép chúng lại thành những hình phức tạp hơn.