Фігури

Нарешті! Ми розвивали попередні навички саме для цього моменту! Ви вивчили більшість основ GLSL мови, її типи та функції. Ви знову й знову практикували свої навички у формотворчих функціях та рівняннях. Настав час зібрати все разом. Ви вже готові прийняти цей виклик! У цьому розділі ви дізнаєтесь, як малювати прості фігури за допомогою паралельних обчислень.

Прямокутник

Уявіть, що ми маємо листок паперу у клітинку, як на уроках математики, і наше домашнє завдання — намалювати квадрат. Розмір паперу 10х10, а квадрат має бути 8х8. Що ви будете робити?

Мабуть, ви б розфарбували все, окрім першого й останнього рядків та першого й останнього стовпців, чи не так?

Як це пов'язано з шейдерами? Кожен маленький квадрат нашої сітки — це один потік (піксель). Кожен квадратик знає своє положення, наче координати на шаховій дошці. У попередніх розділах ми масштабували координати x та y у канали червоного та зеленого кольорів й навчилися використовувати вузьку двовимірну територію масштабовану між 0.0 та 1.0. Як за допомогою цього ми можемо намалювати квадрат відцентрований посередині нашого полотна?

Почнімо з псевдокоду та використання if-операторів для просторових координат. Ці принципи надзвичайно схожі на випадок з паперовим варіантом.

if ((X GREATER THAN 1) AND (Y GREATER THAN 1)) // якщо (x більше 1) та (y більше 1)
    paint white // фарбуємо білим
else // інакше 
    paint black // фарбуємо чорним

Тепер, коли ми маємо краще уявлення про потрібну роботу, замінімо оператор if на step(), а замість використання листка 10x10 використаємо нормалізовані значення між 0.0 і 1.0:

uniform vec2 u_resolution;

void main(){
    vec2 st = gl_FragCoord.xy / u_resolution.xy;
    vec3 color = vec3(0.0);

    // кожен результат поверне 1.0 (білий) або 0.0 (чорний).
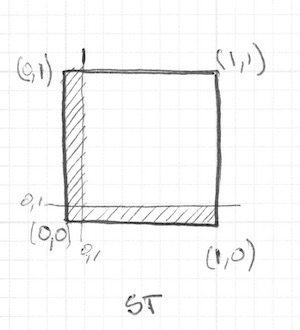
    float left = step(0.1, st.x);   // подібно до (X більше 0.1)
    float bottom = step(0.1, st.y); // подібно до (Y більше 0.1)

    // множення left на bottom спрацює як логічний оператор AND.
    color = vec3(left * bottom);

    gl_FragColor = vec4(color, 1.0);
}

Функція step() перетворить кожен піксель нижче 0.1 на чорний колір (vec3(0.0)), а решту — на білий (vec3(1.0)). Множення між left і bottom працює як логічна операція AND, де обидва значення мають бути рівні 1.0, щоб повернути 1.0. Цей код намалює дві чорні лінії: знизу та зліва.

У попередньому коді ми повторюємо одну і ту ж саму дію для обох сторін: лівої та нижньої. Ми можемо зекономити кілька рядків коду, передавши у step() одразу два значення, у вигляді вектору, замість одного:

vec2 borders = step(vec2(0.1), st);
float pct = borders.x * borders.y;

Поки що ми намалювали лише дві межі нашого прямокутника: нижню та ліву. Зробімо інші дві: верхню та праву. Розгляньте наступний код:

Розкомментуйте рядки 21-22 і подивіться, як ми інвертуємо там координати st і повторюємо ту саму функцію step(). Таким чином vec2(0.0, 0.0) буде у верхньому правому куті. Це цифровий еквівалент перевороту сторінки з повторенням попередньої процедури.

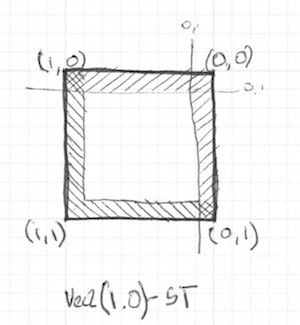
Зверніть увагу, що в рядках 18 і 22 всі сторони перемножуються разом. Це еквівалентно наступному написанню:

vec2 bl = step(vec2(0.1), st);         // нижній-лівий
vec2 tr = step(vec2(0.1), 1.0 - st);   // верхніх-правий
color = vec3(bl.x * bl.y * tr.x * tr.y);

Цікаво правда? Ця техніка базується на використанні step(), множенні у якості логічної операції та перевороті координат.

Перш ніж продовжити, спробуйте виконати такі вправи:

• Змініть розмір і пропорції прямокутника.

• Поекспериментуйте з тим самим кодом, використовуючи smoothstep() замість step(). Зауважте, що змінюючи значення, ви можете переходити від розмитих меж до елегантно згладжених країв.

• Виконайте іншу реалізацію, з використанням floor().

• Виберіть реалізацію, яка вам найбільше до вподоби, та створіть для неї функцію, яку ви зможете повторно використовувати в майбутньому. Зробіть свою функцію гнучкою та ефективною.

• Створіть іншу функцію, яка малюватиме просто контур прямокутника.

• Як можна було б пересувати та розміщувати різні прямокутники на одному полотні? Якщо зрозумієте як це зробити, продемонструйте свої вміння, створивши композицію з прямокутників і кольорів, що нагадує картину Piet Mondrian.

Кола

Легко намалювати квадрати на папері в клітинку та прямокутники за декартовими координатами, але кола вимагають іншого підходу, особливо тому, що нам потрібен "по-піксельний" алгоритм. Одне з рішень полягає в перетворенні просторових координат таким чином, щоб ми змогли використовувати функцію step() для малювання кола.

Як? Почнімо з того, що повернемося до уроку математики та паперу у клітинку. Розкриємо циркуль на радіус кола, поставимо його голку в центрі кола, а потім окреслимо окружність кола простим обертанням.

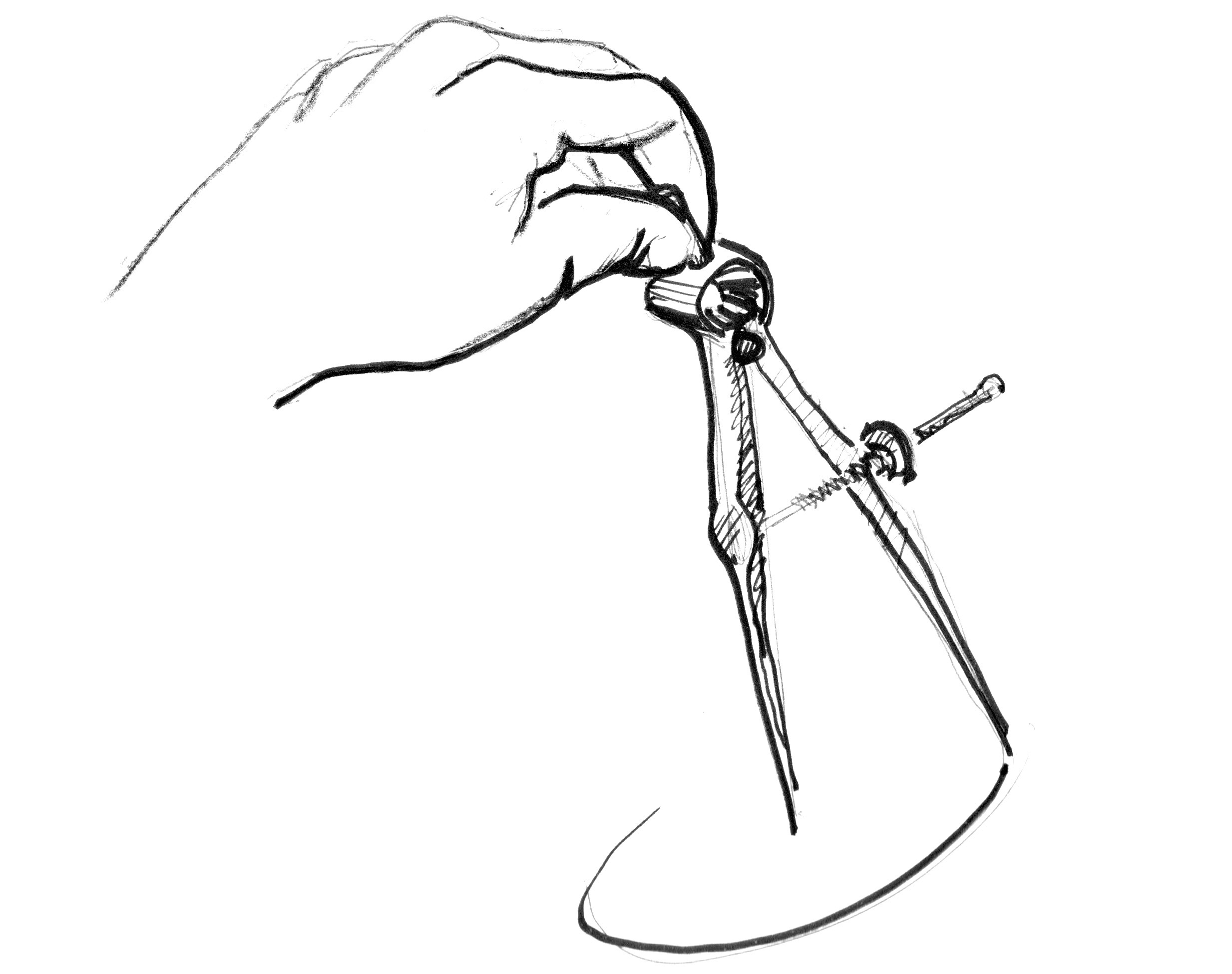
Перекладаючи це на мову шейдера, де кожен квадрат на папері є пікселем, ми маємо спитати кожен піксель (або потік), чи знаходиться він усередині кола. Ми робимо це, обчислюючи відстань від пікселя до центру кола.

Є кілька способів розрахувати цю відстань. Найпростіший використовує функцію distance(), яка всередині обчислює length()-різниці між двома точками. У нашому випадку між координатою пікселя та центром полотна. По своїй суті функція length() — це не що інше, як скорочення для рівняння визначення довжини гіпотенузи, яке використовує квадратний корінь (sqrt()).

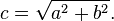
Щоб обчислити відстань до центру полотна ви можете використовувати distance(), length() або sqrt(). Наступний код містить ці три функції та той недивний факт, що кожна з них повертає точно такий самий результат.

• Закоментуйте та розкоментуйте рядки, щоб спробувати різними способами отримати той самий результат.

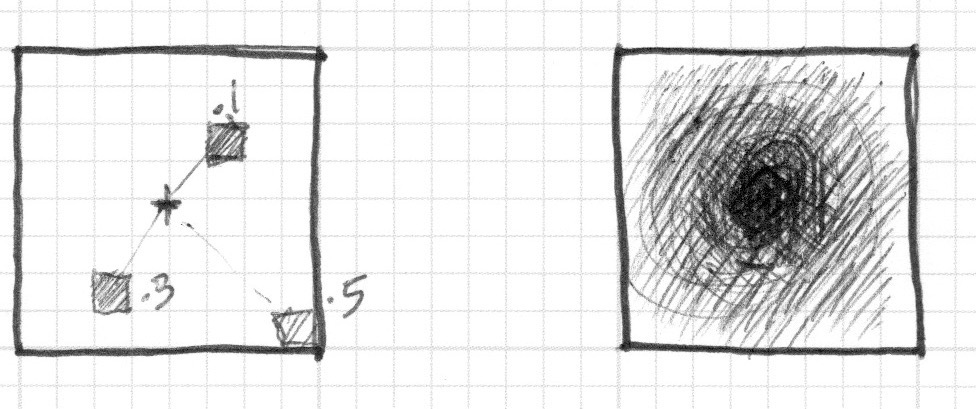
У попередньому прикладі ми переводимо відстань від центру полотна у яскравість кольору пікселя. Чим ближче піксель до центру, тим менше (темніше) значення він має. Зауважте, що значення не стають надто високими, оскільки максимальна відстань від центру (vec2(0.5, 0.5)) ледве перевищує значення 0.5. Подивіться на зображення і подумайте:

• Який висновок ви можете з цього зробити?

• Як ми можемо використати це, щоб намалювати коло?

• Змініть наведений вище код, щоб вмістити весь круговий градієнт всередині полотна.

Поле відстаней

Наведений вище приклад можна розглянути як карту висот, де темніший колір означає вищу позицію. В такому разі цей круговий градієнт буде картою конуса. Уявіть себе на вершині цього конуса. Відстань по горизонталі до краю конуса, в будь-якому напрямку, дорівнює 0.5. Вибираючи, на якій висоті "зрізати" конус, ви отримаєте більший чи менший діаметр кругової поверхні.

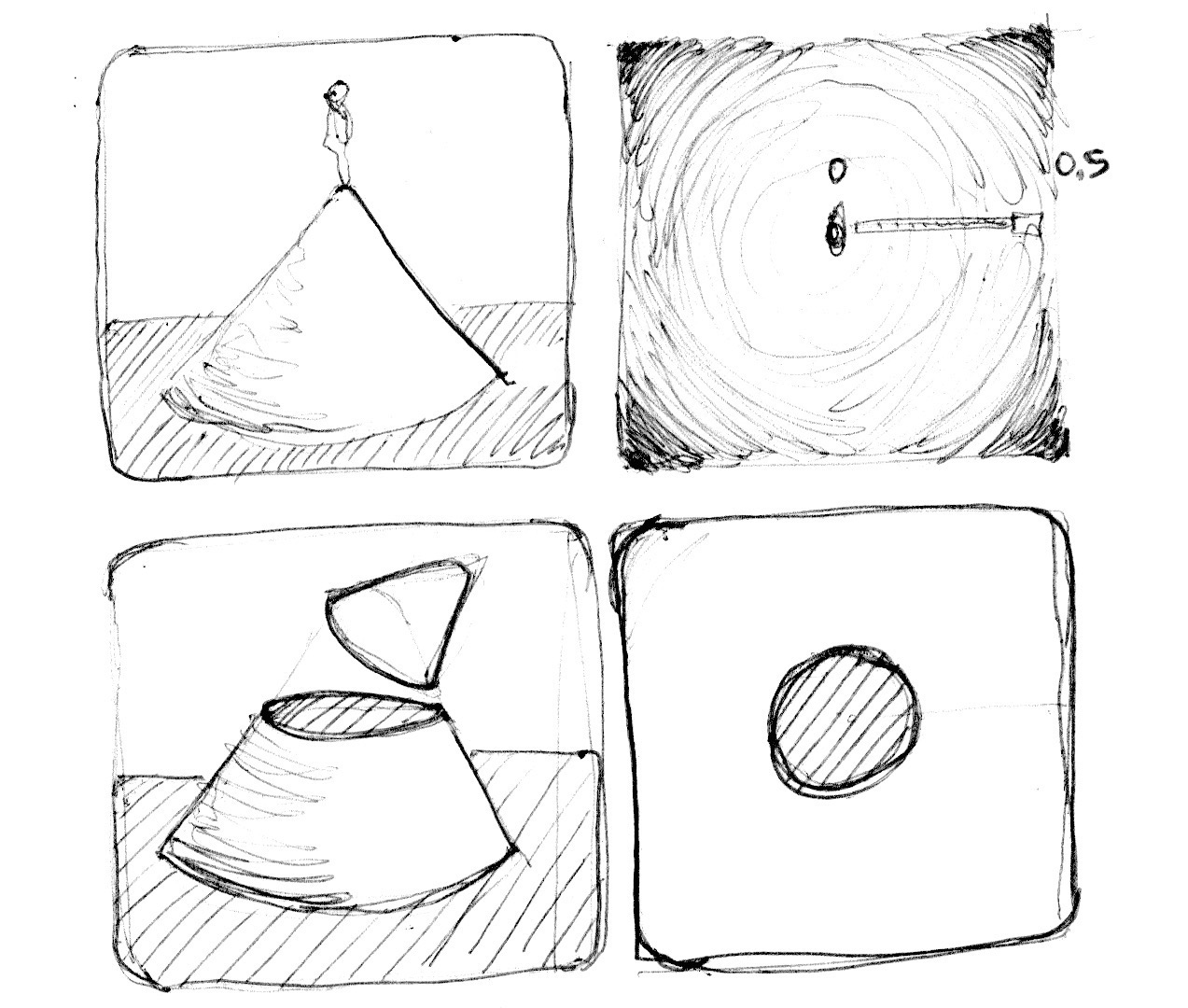
По суті ми інтерпретуємо простір на основі його відстані до центру для того, щоб робити таким чином фігури. Ця техніка відома як "поле відстаней" і використовується різними шляхами, від контурів шрифтів до 3D-графіки.

Спробуйте наступні вправи:

• Використовуйте step(), щоб перетворити значення більші за 0.5 у білий колір, а все, що менше 0.0 — у чорний.

• Змініть місцями кольори фону та переднього плану.

• Використовуючи smoothstep() та експериментуючи з різними значеннями, отримайте гарний плавний край для вашого кола.

• Для найбільш вдалої вашої реалізації створіть функцію, яку ви зможете повторно використовувати в майбутньому.

• Додайте колу колір.

• Чи зможете ви анімувати своє коло, щоб воно збільшувалося та зменшувалося, імітуючи серцебиття? Ви можете отримати натхнення з анімації у попередньому розділі.

• А як щодо переміщення кола? Чи зможете ви перемістити та розташувати на полотні кілька різних кіл?

• Що станеться, якщо скомбінувати поля відстаней за допомогою різних функцій та операцій?

pct = distance(st, vec2(0.4)) + distance(st, vec2(0.6));
pct = distance(st, vec2(0.4)) * distance(st, vec2(0.6));
pct = min(distance(st, vec2(0.4)),distance(st, vec2(0.6)));
pct = max(distance(st, vec2(0.4)),distance(st, vec2(0.6)));
pct = pow(distance(st, vec2(0.4)),distance(st, vec2(0.6)));

• Створіть три композиції за допомоги цієї техніки. Ще краще, якщо вони будуть анімовані!

Для вашого інструментарію

З точки зору обчислювальної потужності, функція sqrt() і всі функції, які від неї залежать, можуть бути досить ресурсовитратними. Ось ще один спосіб для створення кругового поля відстаней за допомогою функції dot().

Корисні властивості поля відстаней

Поля відстаней можна використовувати для малювання майже всього. Очевидно, що чим складнішою є форма, тим складнішим буде її рівняння. Але як тільки у вас є формула для створення поля відстаней певної форми, її дуже легко комбінувати та/або застосовувати до неї ефекти. Наприклад, згладження країв або численні контури. Через це поля відстаней популярні у цифровому зображенні шрифтів, наприклад Mapbox GL Labels, Material Design Fonts (автор: Matt DesLauriers) та iPhone 3D Programming, O’Reilly (див. розділ 7).

Розгляньте наступний код:

Ми починаємо з переміщення відліку системи координат у центр. Звужуємо її вдвічі, щоб вона вміщувала в себе значення позиції між -1.0 та 1.0. Також у рядку 24 ми візуалізуємо значення поля відстаней за допомогою функції fract(), що покаже малюнок форми, який воно створює. Контур поля відстаней повторюється знову і знову, як кільця в саду дзен.

Подивімось на формулу поля відстаней у рядку 19. Тут ми обчислюємо відстань до позиції у точці (.3, .3) (або vec3(.3)) в усіх чотирьох квадрантах (саме для цього було використано abs()).

Якщо ви розкоментуєте рядок 20, то помітите, що ми об'єднуємо відстані до цих чотирьох точок за допомогою функції min() до нуля. У результаті виходить новий цікавий візерунок.

Тепер спробуйте розкоментувати рядок 21. Тут ми робимо те саме, але використовуємо функцію max(). В результаті вийде прямокутник із закругленими кутами. Зверніть увагу, що кільця поля відстаней стають більш гладкими, чим далі вони віддаляються від центру.

Нарешті, по черзі розкоментуйте рядки з 27 по 29, щоб побачити та зрозуміти різні варіанти шаблонів використання поля відстаней.

Фігури у полярних координатах

У розділі про колір ми зіставляли декартові координати з полярними координатами, обчислюючи радіус і кут кожного пікселя за такою формулою:

vec2 pos = vec2(0.5) - st;
float r = length(pos) * 2.0;
float a = atan(pos.y, pos.x);

На початку розділу ми використали частину цієї формули, щоб намалювати коло. Ми обчислили відстань до центру за допомогою функції length(). Тепер, знаючи про поля відстаней, ми можемо навчитися малювати фігури за допомогою полярних координат іншим способом.

Ця техніка трохи обмежена, але дуже проста. Вона полягає в отримання різних форм, змінюючи радіус кола залежно від кута. Як це працює? Звісно ж за допомогою функцій формування!

Нижче ви знайдете функції для отримання значень у декартовій системі координат та зображення їх на графіку. А ще нижче інший приклад з тими ж самими функціями, але вже для полярних координат (між рядками 21 і 25). Розкоментуйте ці функції одну за одною та звертайте увагу на співвідношення між обома системами координат.

Спробуйте:

• Анімувати ці форми.
• Комбінувати різні формотворчі функції, щоб вирізати отвори у формі й зробити подобу квітів, сніжинок та шестерень.
• Використати функцію plot() з розділу Формотворчих функцій, щоб намалювати лише контур.

Сила комбінацій

Ми навчилися модулювати радіус кола відповідно до кута за допомогою функції atan() для малювання різних фігур. Тепер ми можемо навчитися використовувати atan() з полями відстаней та застосувати всі трюки та ефекти, можливі з цими полями.

Наступний трюк використовує кількість ребер багатокутника для побудови поля відстаней за допомогою полярних координат. Перегляньте цей код від Andrew Baldwin.

• Використовуючи цей приклад, створіть функцію, яка приймає положення та кількість кутів потрібного багатокутника й повертає значення поля відстаней.

• Змішайте поля відстаней за допомогою функції min() та max().

• Виберіть геометричний логотип і відтворіть його за допомогою полей відстані.

Щиро вітаю! Ви пройшли через складну частину! Зробіть перерву й дайте цим концепціям засвоїтись. Так, малювати прості фігури десь у Processing легко, але не тут. У світі шейдерів малювання фігур хитромудра справа, і адаптація до цієї нової парадигми кодування може бути виснажливою.

У кінці цього розділу ви знайдете посилання на Колоду PixelSpirit. Ця колода карт допоможе вам вивчити нові функції SDF, скомпонувати їх та використати у ваших шейдерах. Колода має прогресивну криву навчання. Можете брати по одній карті на день й опрацьовувати її, щоб підштовхнути та випробувати свої навички.

Тепер, коли ви знаєте, як малювати фігури, я впевнений, що у вас у голові з’являться нові ідеї. У наступному розділі ви дізнаєтесь, як переміщувати, обертати та масштабувати фігури. Це дозволить вам складати композиції!