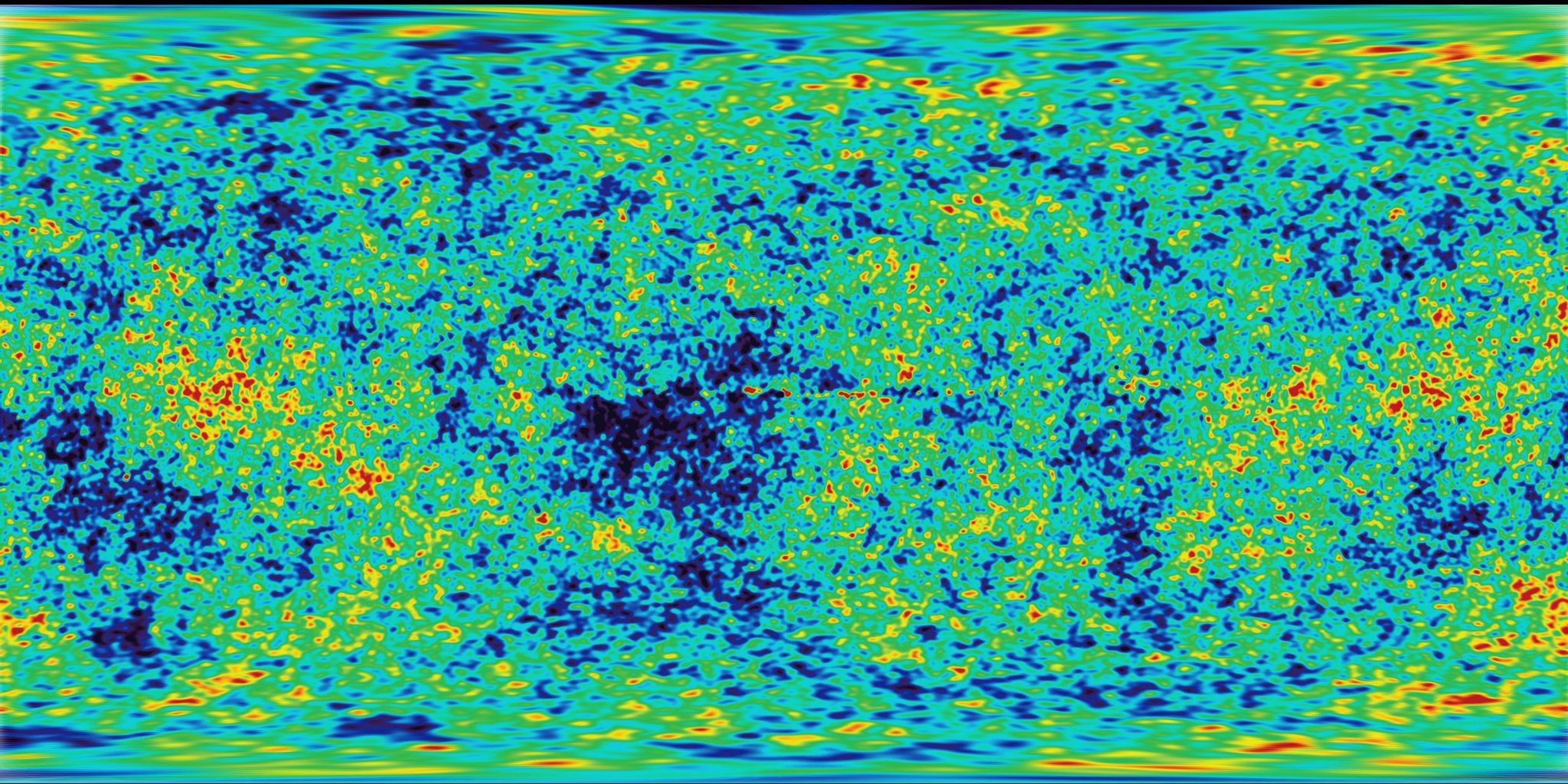
Noise

Waktunya istirahat! kita telah bermain dengan fungsi acak yang terlihat seperti derau putih TV, kepala kita masih berputar memikirkan shader, dan mata kita lelah. Waktunya jalan-jalan keluar!

kita merasakan udara di kulit kita, matahari di wajah kita. Dunia adalah tempat yang hidup dan kaya. Warna, tekstur, suara. Saat kita berjalan kita tidak dapat menghindari memperhatikan permukaan jalan, bebatuan, pepohonan dan awan.

Ketidakpastian tekstur ini bisa disebut "acak", tetapi tidak terlihat seperti acak yang kita mainkan sebelumnya. “Dunia nyata” adalah tempat yang kaya dan kompleks! Bagaimana kita bisa memperkirakan variasi ini secara komputasi?

Ini adalah pertanyaan yang coba dipecahkan oleh Ken Perlin pada awal 1980-an ketika dia ditugaskan untuk menghasilkan tekstur yang lebih realistis untuk film "Tron". Menanggapi itu, dia datang dengan algoritma suara pemenang Oscar yang elegan. (Bukan masalah besar.)

Berikut ini bukanlah algoritma derau Perlin klasik, tetapi ini adalah titik awal yang baik untuk memahami cara menghasilkan derau.

Dalam baris ini kita melakukan sesuatu yang mirip dengan apa yang kita lakukan di bab sebelumnya. kita membagi bilangan mengambang kontinu (x) menjadi komponen bilangan bulat (i) dan pecahan (f). kita menggunakan floor() untuk mendapatkan i dan fract() untuk mendapatkan f. Kemudian kita menerapkan rand() ke bagian integer dari x, yang memberikan nilai acak unik untuk setiap integer.

Setelah itu Anda melihat dua baris yang diberi komentar. Yang pertama menginterpolasi setiap nilai acak secara linier.

y = mix(rand(i), rand(i + 1.0), f);

Lanjutkan dan hapus komentar pada baris ini untuk melihat tampilannya. kita menggunakan penyimpanan nilai `fract()` di f hingga mix() dua nilai acak.

Pada poin di buku ini, kita telah belajar bahwa kita bisa melakukan lebih baik daripada interpolasi linier, bukan? Sekarang coba hapus komentar pada baris berikut, yang menggunakan interpolasi smoothstep() alih-alih yang linier.

y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f));

Setelah menghapus komentar, perhatikan bagaimana transisi antara puncak menjadi mulus. Dalam beberapa implementasi noise, Anda akan menemukan bahwa programmer lebih suka membuat kode kurva kubik mereka sendiri (seperti rumus berikut) daripada menggunakan smoothstep().

float u = f * f * (3.0 - 2.0 * f ); // custom cubic curve
y = mix(rand(i), rand(i + 1.0), u); // using it in the interpolation

Keacakan halus ini adalah pengubah permainan untuk insinyur atau seniman grafis - ini memberikan kemampuan untuk menghasilkan gambar dan geometri dengan perasaan organik. Algoritma noise Perlin telah diterapkan berulang kali dalam berbagai bahasa dan dimensi untuk membuat karya yang memukau untuk semua jenis penggunaan kreatif.

Sekarang giliran Anda:

• Buat fungsi float noise(float x) Anda sendiri.

• Gunakan fungsi noise Anda untuk menganimasikan bentuk dengan memindahkannya, memutarnya, atau menskalakannya.

• Buat komposisi animasi dari beberapa bentuk 'menari' bersama menggunakan noise.

• Bangun bentuk "yang terlihat organik" menggunakan fungsi noise.

• Setelah Anda memiliki "makhluk" Anda, cobalah untuk mengembangkannya lebih jauh menjadi karakter dengan memberinya gerakan tertentu.

Noise 2D

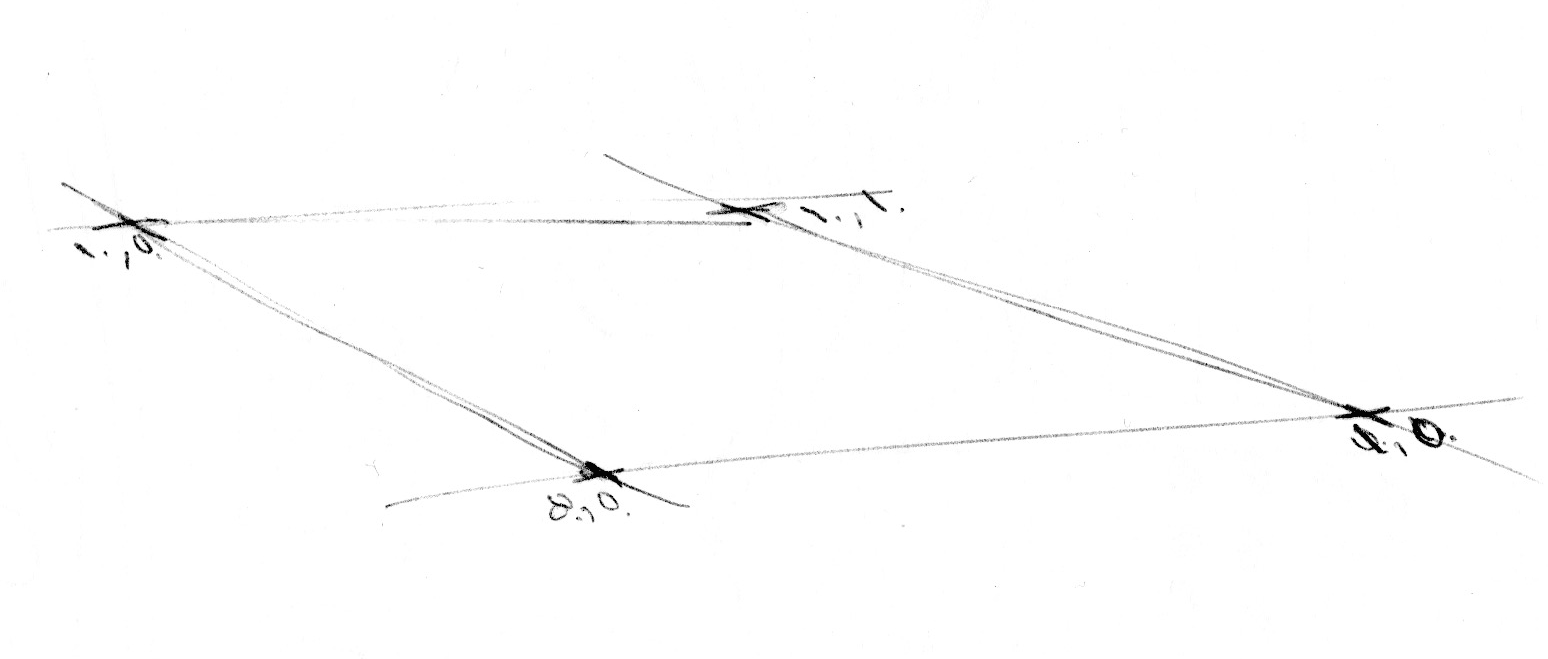
Sekarang kita tahu bagaimana melakukan noise dalam 1D, sekarang saatnya beralih ke 2D. Dalam 2D, alih-alih melakukan interpolasi antara dua titik garis (fract(x) dan fract(x)+1.0), kita akan melakukan interpolasi di antara empat sudut persegi luas bidang (fract(st), fract(st)+vec2(1.,0.), fract(st)+vec2(0.,1.) dan fract(st)+vec2(1.,1.)).

Demikian pula, jika kita ingin mendapatkan noise 3D, kita perlu melakukan interpolasi antara delapan sudut kubus. Teknik ini adalah tentang interpolasi nilai acak, itulah sebabnya disebut noise nilai.

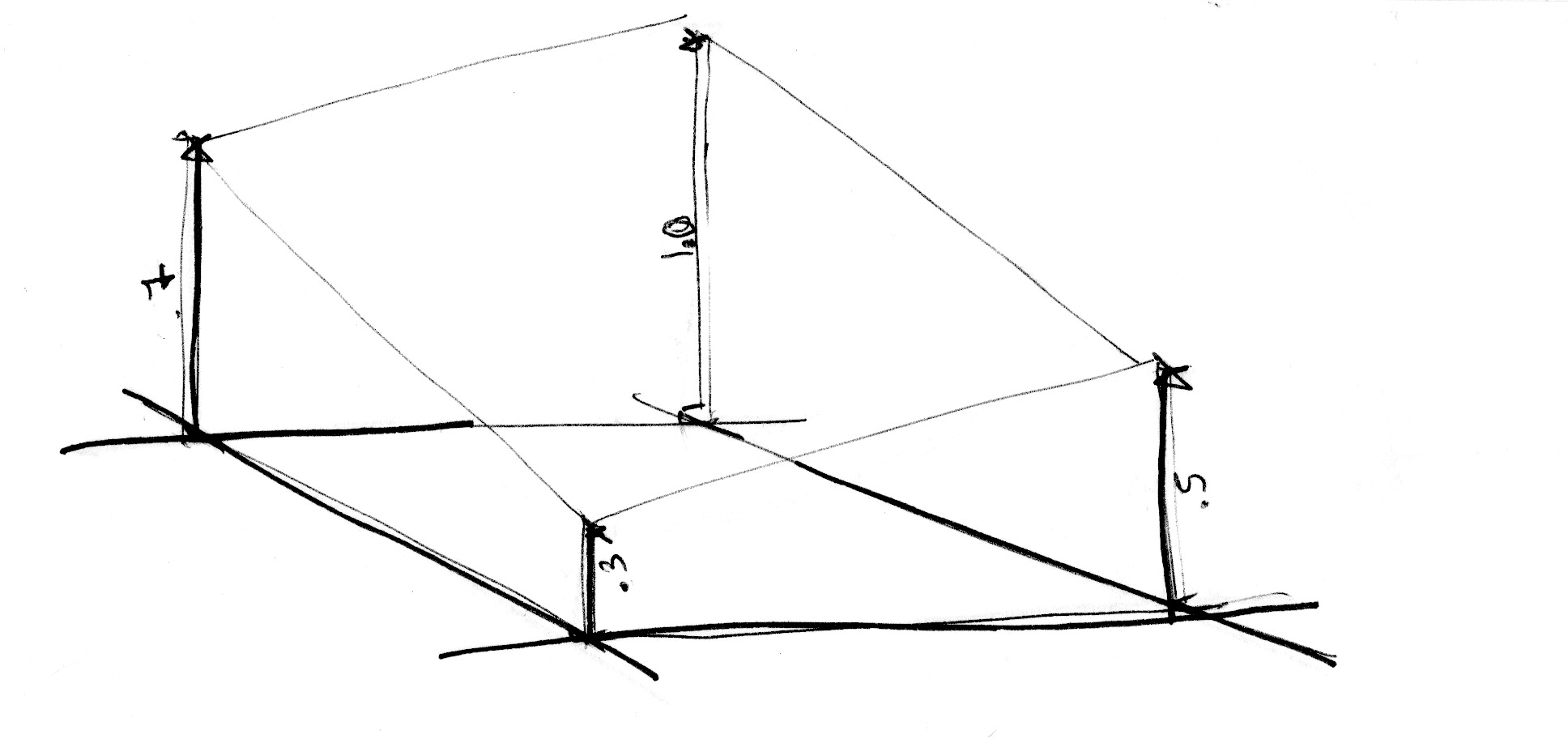
Seperti contoh 1D, interpolasi ini tidak linier tetapi kubik, yang dengan mulus menginterpolasi setiap titik di dalam kisi persegi kita.

Perhatikan fungsi noise berikut.

Kita mulai dengan menskalakan ruang dengan 5 (baris 45) untuk melihat interpolasi antara kotak dari kisi. Kemudian di dalam fungsi noise kita membagi ruang menjadi sel. kita menyimpan posisi integer sel bersama dengan posisi pecahan di dalamn sel. kita menggunakan posisi integer untuk menghitung koordinat empat penjuru dan mendapatkan nilai acak untuk masing-masing (baris 23-26). Akhirnya, pada baris 35 kita melakukan interpolasi antara 4 nilai acak dari sudut menggunakan posisi pecahan yang kita simpan sebelumnya.

Sekarang giliranmu. Coba latihan berikut:

• Ubah pengali baris 45. Cobalah untuk menghidupkannya.

• Pada tingkat zoom berapa noise mulai terlihat seperti acak lagi?

• Pada tingkat zoom apakah noise tidak terlihat?

• Cobalah untuk menghubungkan fungsi noise ini ke koordinat mouse.

• Bagaimana jika kita memperlakukan gradien noise sebagai bidang jarak? Buatlah sesuatu yang menarik dengannya.

• Sekarang setelah Anda mencapai kendali atas keteraturan dan kekacauan, inilah saatnya untuk menggunakan pengetahuan itu. Buat komposisi persegi panjang, warna, dan derau yang menyerupai kerumitan lukisan Mark Rothko.

Menggunakan Noise dalam Desain Generatif

Algoritme noise pada awalnya dirancang untuk memberikan je ne sais quoi alami pada tekstur digital. Implementasi 1D dan 2D yang telah kita lihat sejauh ini adalah interpolasi antara nilai acak, itulah sebabnya disebut Noise Nilai, tetapi ada lebih banyak cara untuk mendapatkan noise ...

Seperti yang Anda temukan di latihan sebelumnya, noise nilai cenderung terlihat "kotak-kotak". Untuk mengurangi efek blok ini, pada tahun 1985 Ken Perlin mengembangkan implementasi lain dari algoritme yang disebut Gradient Noise. Ken menemukan cara menginterpolasi gradien acak daripada nilai. Gradien ini adalah hasil dari fungsi acak 2D yang mengembalikan arah (diwakili oleh vec2), bukan nilai tunggal (float). Klik pada gambar berikut untuk melihat kode dan cara kerjanya.

Luangkan waktu sejenak untuk melihat kedua contoh oleh Inigo Quilez dan perhatikan perbedaan antara [value noise](https://www.shadertoy.com/view/ lsf3WH) dan noise gradien.

Seperti seorang pelukis yang memahami cara kerja pigmen pada catnya, semakin banyak yang kita ketahui tentang penerapan noise, semakin baik kita dapat menggunakannya. Misalnya, jika kita menggunakan implementasi noise dua dimensi untuk memutar ruang tempat garis lurus dirender, kita dapat menghasilkan efek swirly berikut yang terlihat seperti kayu. Sekali lagi Anda dapat mengklik gambar untuk melihat seperti apa kodenya.

    color += smoothstep(.15,.2,noise(st*10.)); // Black splatter
    color -= smoothstep(.35,.4,noise(st*10.)); // Holes on splatter

Cara lain untuk mendapatkan pola menarik dari noise adalah dengan memperlakukannya seperti bidang jarak dan menerapkan beberapa trik yang dijelaskan dalam bab Bentuk.

    color += smoothstep(.15,.2,noise(st*10.)); // Black splatter
    color -= smoothstep(.35,.4,noise(st*10.)); // Holes on splatter

Cara ketiga menggunakan fungsi derau adalah memodulasi bentuk. Ini juga membutuhkan beberapa teknik yang kita pelajari di [bab tentang bentuk] (../ 07 /).

Untuk Anda berlatih:

• Pola generatif lain apa yang dapat Anda buat? Bagaimana dengan granit? marmer? magma? air? Temukan tiga gambar tekstur yang Anda minati dan terapkan secara algoritme menggunakan noise.
• Gunakan noise untuk memodulasi bentuk.
• Bagaimana dengan menggunakan noise untuk gerakan? Kembali ke [bab Matrix] (../08/). Gunakan contoh terjemahan yang menggerakkan "+", dan terapkan beberapa gerakan acak dan gangguan padanya.
• Buat Jackson Pollock generatif.

Peningkatan Noise

Peningkatan oleh Perlin ke noise non-simpleks aslinya noise Simpleks, adalah penggantian kurva Hermite kubik ( f(x) = 3x^2-2x^3, yang identik dengan fungsi smoothstep()) dengan kurva interpolasi kuintik ( f(x) = 6x^5-15x^4+10x^3 ). Hal ini membuat kedua ujung kurva lebih "rata" sehingga setiap tepi jahitan dengan anggun dengan ujung berikutnya. Dengan kata lain, Anda mendapatkan transisi yang lebih berkelanjutan antar sel. Anda dapat melihatnya dengan menghapus komentar rumus kedua pada contoh grafik berikut (atau lihat [dua persamaan berdampingan di sini] (https://www.desmos.com/calculator/2xvlk5xp8b)).

Perhatikan bagaimana ujung kurva berubah. Anda dapat membaca lebih lanjut tentang ini di Ken's own words

Noise Simpleks

Bagi Ken Perlin, keberhasilan algoritmanya tidak cukup. Dia pikir itu bisa bekerja lebih baik. Di Siggraph 2001 dia mempresentasikan "gangguan simpleks" di mana dia mencapai peningkatan berikut dari algoritme sebelumnya:

• Algoritme dengan kompleksitas komputasi yang lebih rendah dan perkalian yang lebih sedikit.
• noise yang berskala ke dimensi yang lebih tinggi dengan biaya komputasi yang lebih sedikit.
• Suara tanpa artefak arah.
• noise dengan gradien yang terdefinisi dengan baik dan berkelanjutan yang dapat dihitung dengan cukup murah.
• Algoritme yang mudah diterapkan di perangkat keras.

Saya tahu apa yang Anda pikirkan ... "Siapa pria ini?" Ya, karyanya luar biasa! Tapi serius, bagaimana dia meningkatkan algoritme? Nah, kita melihat bagaimana untuk dua dimensi dia menginterpolasi 4 titik (sudut persegi); jadi kita bisa menebak dengan benar bahwa untuk tiga (lihat implementasinya di sini) dan empat dimensi kita perlu menginterpolasi 8 dan 16 poin. Baik? Dengan kata lain untuk dimensi N Anda perlu menginterpolasi 2 ke titik N(2^N) dengan mulus. Tetapi Ken dengan cerdas memperhatikan bahwa meskipun pilihan yang jelas untuk bentuk pengisi ruang adalah persegi, bentuk paling sederhana dalam 2D ​​adalah segitiga sama sisi. Jadi dia mulai dengan mengganti kisi kuadrat (kita baru saja belajar cara menggunakannya) untuk kisi simpleks segitiga sama sisi.

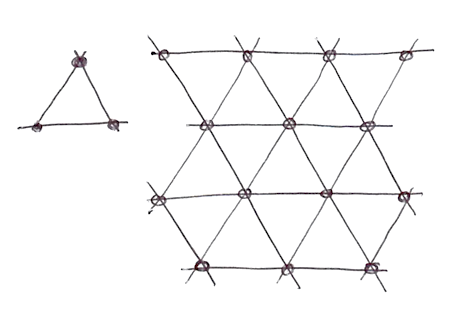
Bentuk simpleks untuk dimensi N adalah bentuk dengan sudut N + 1. Dengan kata lain, satu sudut lebih sedikit untuk dihitung dalam 2D, 4 sudut lebih sedikit dalam 3D dan 11 sudut lebih sedikit dalam 4D! Itu peningkatan yang sangat besar!

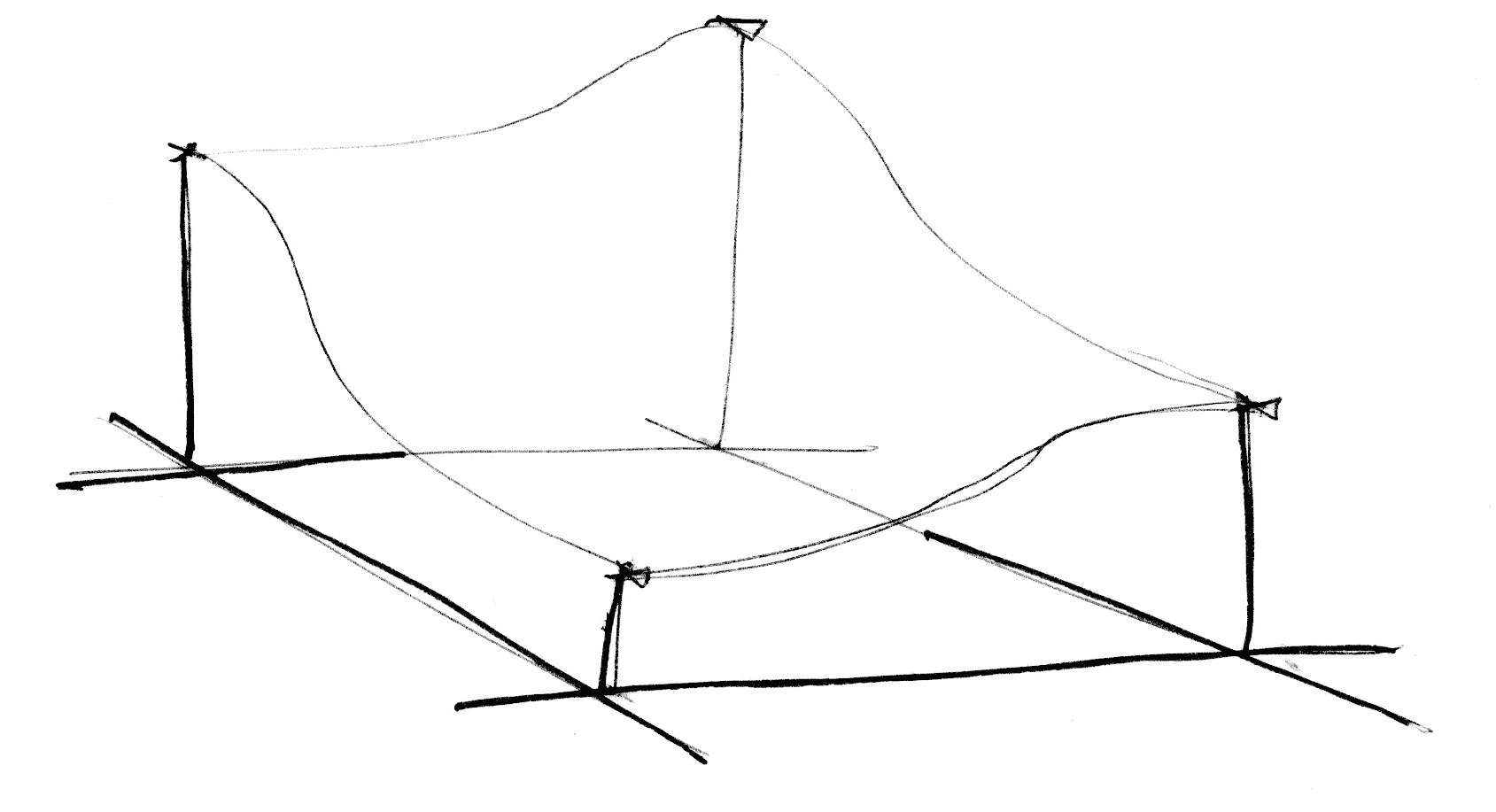
Dalam dua dimensi, interpolasi terjadi serupa dengan noise biasa, dengan menginterpolasi nilai sudut suatu bagian. Namun dalam hal ini, dengan menggunakan grid simpleks, kita hanya perlu melakukan interpolasi dari jumlah 3 sudut saja.

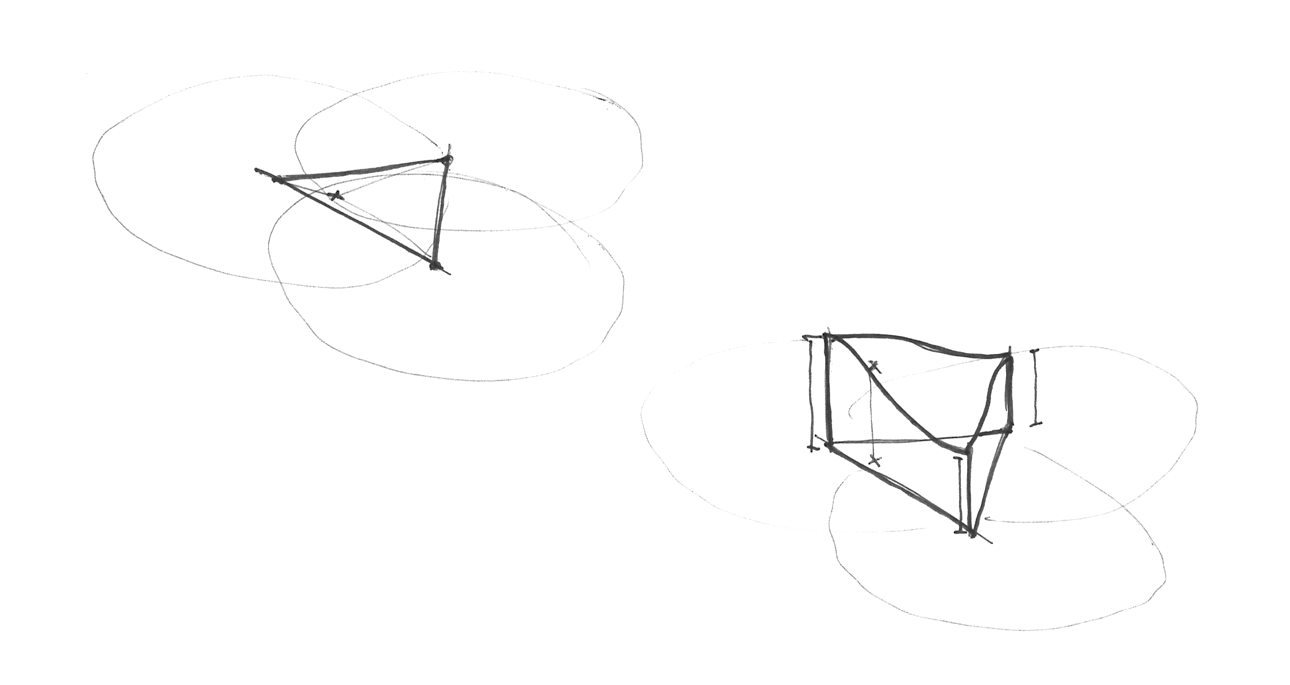
Bagaimana jaringan simpleks dibuat? Dalam langkah brilian dan elegan lainnya, kisi simpleks dapat diperoleh dengan membagi sel-sel dari kisi bersudut 4 biasa menjadi dua segitiga sama kaki dan kemudian memiringkannya hingga setiap segitiga sama sisi.

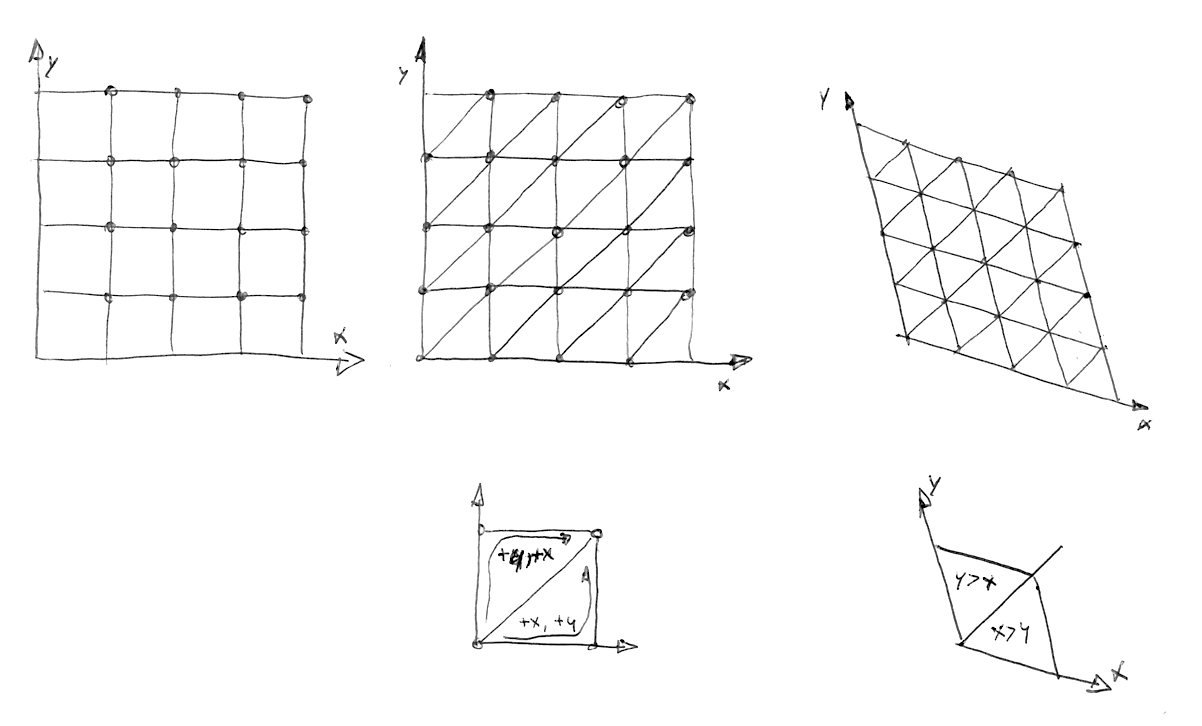
Kemudian, seperti yang Stefan Gustavson gambarkan dalam makalah ini: "... dengan melihat bagian bilangan bulat dari koordinat yang ditransformasikan (x, y) untuk titik yang ingin kita evaluasi, kita dapat dengan cepat menentukan sel mana dari dua sederhana yang berisi titik. Dengan juga membandingkan besaran x dan y, kita dapat menentukan apakah titik tersebut ada di simplex atas atau bawah , dan melintasi tiga titik sudut yang benar. "

Dalam kode berikut, Anda dapat menghapus komentar baris 44 untuk melihat bagaimana kisi miring, dan kemudian menghapus komentar baris 47 untuk melihat bagaimana kisi simpleks dapat dibangun. Perhatikan bagaimana pada baris 22 kita membagi persegi miring menjadi dua segitiga sama sisi hanya dengan mendeteksi jika x > y (segitiga "bawah ") atau`y > x (segitiga "atas").

Semua peningkatan ini menghasilkan mahakarya algoritmik yang dikenal sebagai Simplex Noise. Berikut ini adalah implementasi GLSL dari algoritma ini yang dibuat oleh Ian McEwan dan Stefan Gustavson (dan disajikan dalam makalah ini) yang terlalu rumit untuk tujuan pendidikan, tetapi Anda akan dengan senang hati mengekliknya dan melihat bahwa itu kurang samar dari yang Anda harapkan, dan kodenya pendek dan cepat.

Yah... cukup teknis, inilah saatnya Anda menggunakan sumber daya ini dengan cara ekspresif Anda sendiri:

• Renungkan bagaimana setiap implementasi noise terlihat. Bayangkan mereka sebagai bahan mentah, seperti batu marmer untuk pematung. Apa yang dapat Anda katakan tentang "perasaan" yang dimiliki masing-masing? Tutup mata Anda untuk memicu imajinasi Anda, seperti saat Anda ingin menemukan bentuk di awan. Apa yang kamu lihat? Anda diingatkan tentang apa? Menurut Anda, setiap implementasi noise dapat dibuat menjadi apa? Ikuti nyali Anda dan cobalah untuk mewujudkannya dalam kode.

• Buat shader yang memproyeksikan ilusi aliran. Seperti lampu lava, tetesan tinta, air, dll.

• Gunakan Simplex Noise untuk menambahkan tekstur pada karya yang telah Anda buat.

Dalam bab ini kita telah memperkenalkan beberapa kendali atas kekacauan. Itu bukanlah pekerjaan yang mudah! Menjadi ahli penyok noise membutuhkan waktu dan usaha.

Dalam bab-bab berikut, kita akan melihat beberapa teknik terkenal untuk menyempurnakan keterampilan Anda dan memaksimalkan noise Anda untuk merancang konten generatif berkualitas dengan shader. Sampai saat itu nikmati waktu di luar sambil merenungkan alam dan polanya yang rumit. Kemampuan Anda untuk mengamati membutuhkan dedikasi yang sama (atau mungkin lebih) daripada keterampilan membuat Anda. Pergilah keluar dan nikmati sisa hari ini!

"Bicaralah dengan pohon, bertemanlah dengannya." Bob Ross