Noise (pol. "szum")

Czas na przerwę! Bawiliśmy się losowymi funkcjami, które wyglądają jak szum telewizyjny (tzw. "szum biały", ang. "white noise"), w głowie wciąż się kręci od myślenia o shaderach, a oczy są po prostu zmęczone. Czas wyjść na spacer!

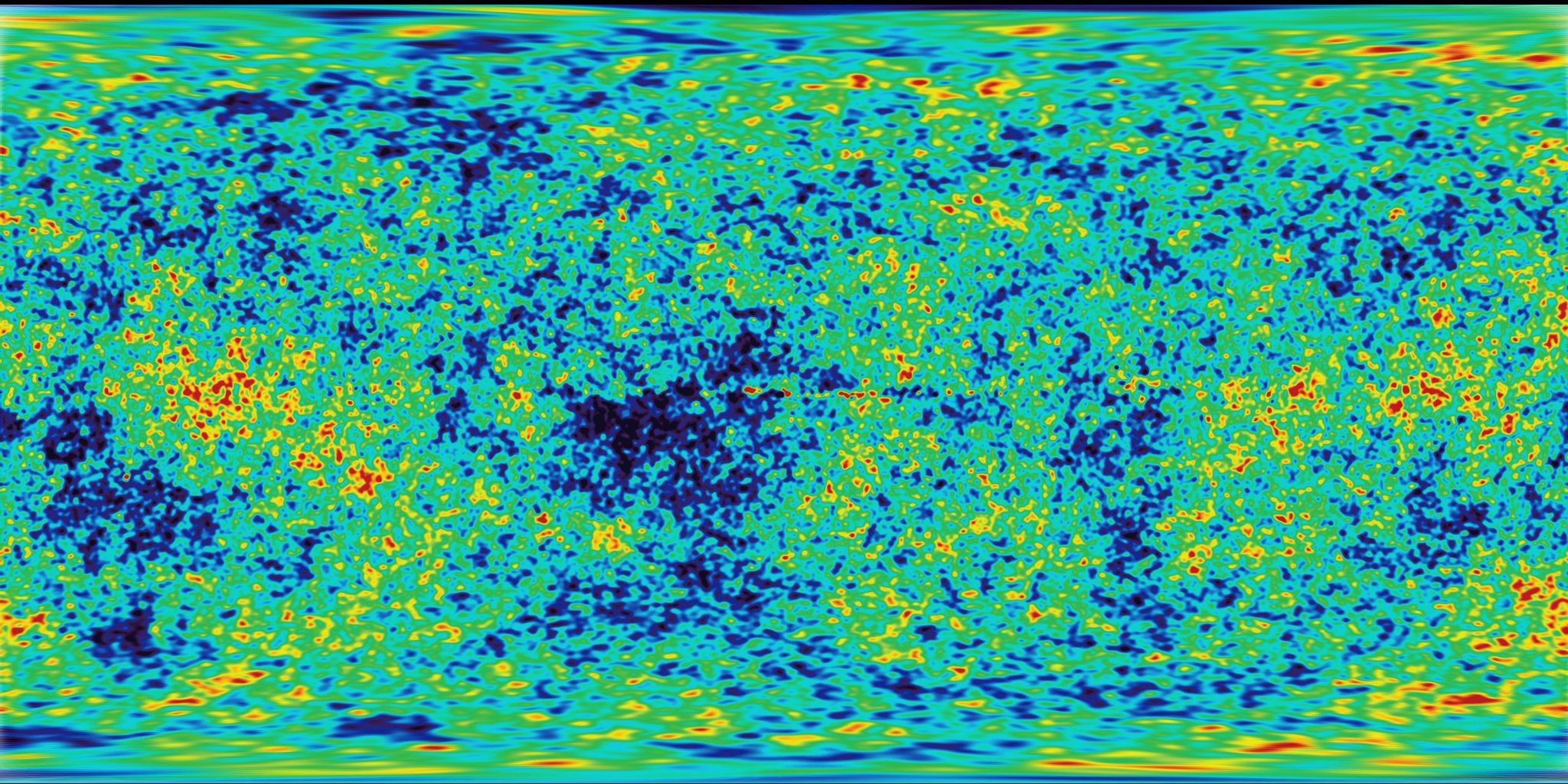
Czujemy powietrze na skórze, słońce na twarzy. Świat jest tak żywym i bogatym miejscem. Kolory, tekstury, dźwięki. Podczas spaceru widzimy powierzchnię dróg, skał, drzew i chmur.

Nieprzewidywalność tych tekstur można by nazwać "losową", ale nie przypominają one losowości, z którą bawiliśmy się wcześniej. "Prawdziwy świat" jest tak bogatym i złożonym miejscem! Jak możemy zamodelować tę różnorodność obliczeniowo?

To było pytanie, które Ken Perlin próbował rozwiązać we wczesnych latach 80-tych, kiedy otrzymał zlecenie wygenerowania bardziej realistycznych tekstur do filmu "Tron". W odpowiedzi na to wymyślił elegancki algorytm szumu, za który później otrzymał Oskara.

Poniższy kod nie jest klasycznym algorytmem szumu Perlina, ale jest dobrym punktem wyjścia do zrozumienia sposobu generowania szumu.

W tych liniach robimy coś podobnego do tego, co robiliśmy w poprzednim rozdziale. Dzielimy ciągłą liczbę zmiennoprzecinkową (x) na jej składowe całkowitą (i) i ułamkową (f). Używamy floor() aby uzyskać i oraz fract() aby uzyskać f. Następnie stosujemy rand() do części całkowitej x, co daje unikalną wartość losową dla każdej liczby całkowitej.

Spójrz na dwie skomentowane linie. Pierwsza z nich interpoluje liniowo każdą wartość losową.

y = mix(rand(i), rand(i + 1.0), f);

Odkomentuj tę linię, aby zobaczyć jak to wygląda. Używamy f do interpolacji liniowej dwóch sąsiadujących wartości losowych za pomocą funkcji mix().

Nauczyliśmy się, że możemy zrobić coś lepszego niż interpolacja liniowa, prawda? Spróbuj teraz odkomentować kolejną drugą linię, która używa interpolacji smoothstep() zamiast liniowej.

y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f));

Po odkomentowaniu zauważ, jak przejście między szczytami staje się gładkie. W niektórych implementacjach szumu można zauważyć, że programiści wolą kodować własne krzywe sześcienne (ang. "cubic curves") (jak w kodzie poniżej) zamiast używać smoothstep().

float u = f * f * (3.0 - 2.0 * f ); // spersonalizowana funkcja sześcienna
y = mix(rand(i), rand(i + 1.0), u); // interpolacja z jej pomocą

Ta płynna losowość jest przełomem dla programistów grafiki i artystów - daje możliwość generowania organicznych obrazów i geometrii. Algorytm Szumu Perlina był wielokrotnie implementowany w różnych językach i wymiarach, aby móc tworzyć hipnotyzujące dzieła w celach kreatywnych.

Teraz twoja kolej:

• Stwórz własną funkcję float noise(float x).

• Użyj swojej funkcji szumu do animowania kształtu poprzez przesuwanie go, obracanie lub skalowanie.

• Zrób animowaną kompozycję kilku kształtów "tańczących" razem przy użyciu szumu.

• Skonstruuj "organicznie wyglądające" kształty używając funkcji noise.

Szum 2D

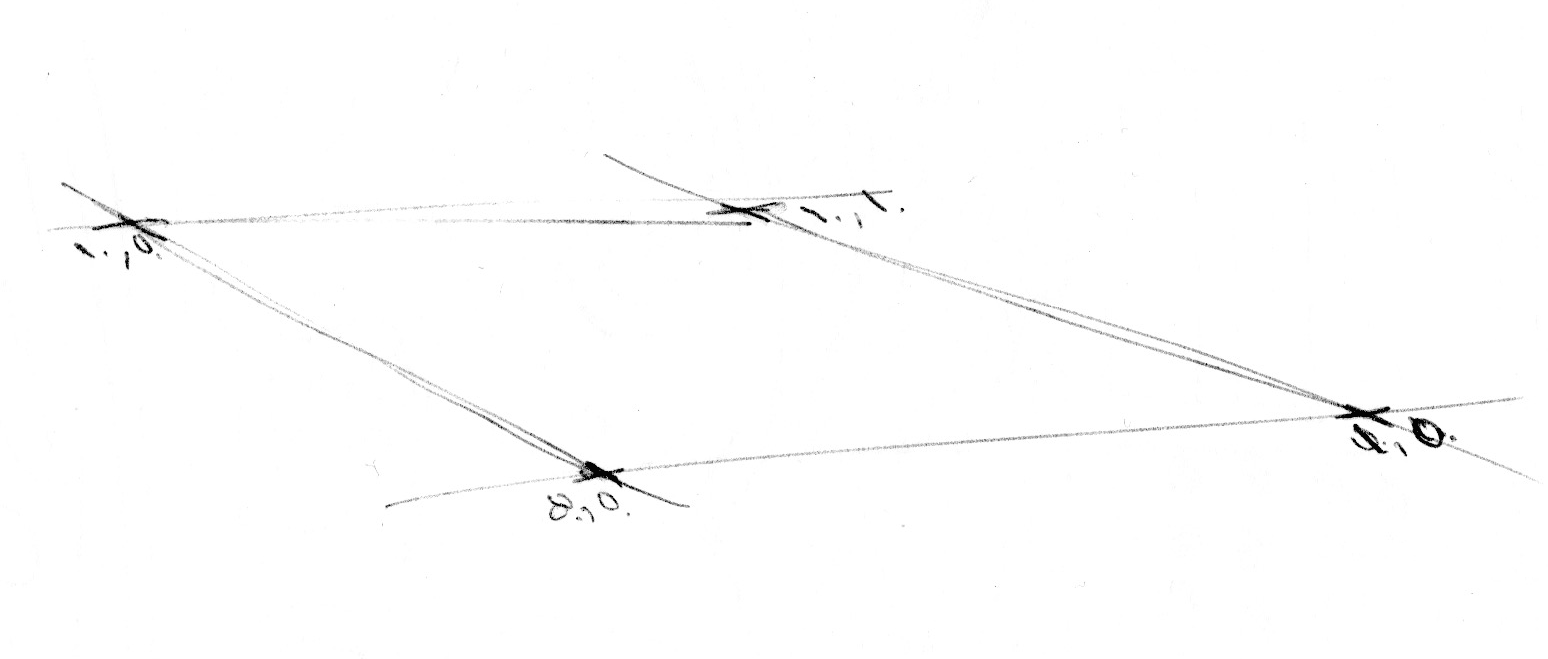
Teraz, gdy wiemy jak zrobić szum w 1D, czas przejść do 2D. W 2D zamiast interpolować między dwoma punktami linii (rand(x) i rand(x)+1.0), będziemy interpolować pomiędzy czterema narożnikami kwadratowego obszaru płaszczyzny (rand(st), rand(st)+vec2(1.,0.), rand(st)+vec2(0.,1.) oraz rand(st)+vec2(1.,1.)).

Podobnie, jeśli chcemy uzyskać szum 3D musimy interpolować pomiędzy ośmioma rogami sześcianu. W tej technice chodzi o interpolację losowych wartości ang. (ang. "random values"), dlatego nazywa się ją value noise.

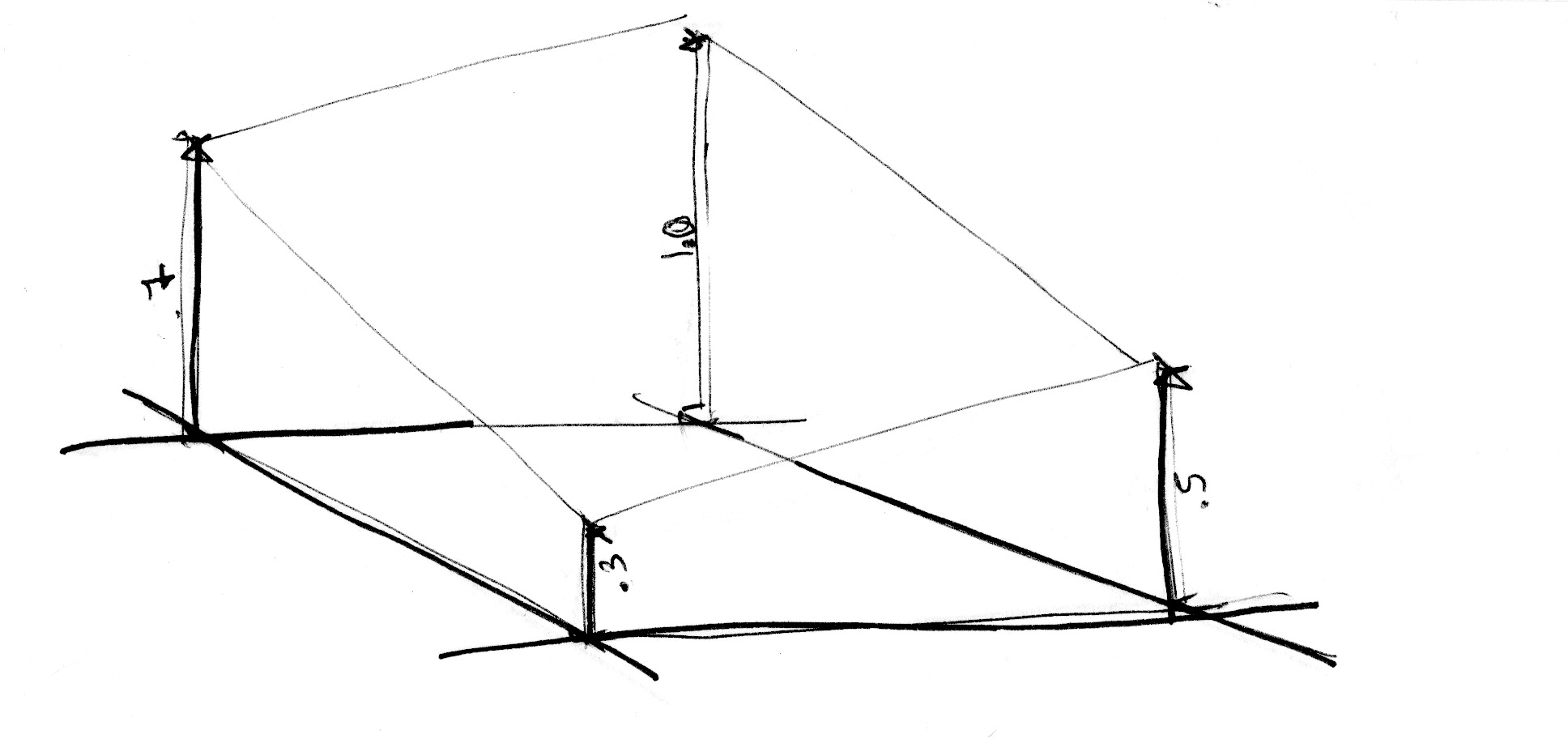
Podobnie jak w przykładzie 1D, interpolacja ta nie jest liniowa, ale sześcienna, więc płynnie interpoluje wszelkie punkty wewnątrz naszego kwadratowego obszaru.

Przyjrzyj się następującej funkcji szumu.

Zaczynamy od przeskalowania przestrzeni o 5 (linia 45). Następnie wewnątrz funkcji szumu dzielimy przestrzeń na kafellki. Przechowujemy pozycję kafelka jako cześć całkowitą oraz pozycje wewnątrz kafelka jako część ułamkową. Używamy części całkowitej do obliczenia współrzędnych czterech narożników, otrzymując losową wartość dla każdego z nich (linie 23-26). Na koniec, w linii 35 interpolujemy pomiędzy 4 losowymi wartościami narożników używając części ułamkowej.

Teraz twoja kolej. Spróbuj wykonać następujące ćwiczenia:

• Zmień mnożnik w linii 45. Spróbuj go zanimować.

• Przy jakim poziomie powiększenia szum zaczyna znowu wyglądać kompletnie losowo (jak, wspomniany na początku rozdziału, biały szum)?

• Przy jakim poziomie powiększenia szum jest niezauważalny?

• Spróbuj podpiąć tę funkcję szumu do współrzędnych myszy.

• A gdyby tak potraktować gradient szumu jako pole odległości? Zrób z tym coś ciekawego.

• Teraz, gdy osiągnąłeś już pewną kontrolę nad porządkiem i chaosem, czas wykorzystać tę wiedzę. Stwórz kompozycję z prostokątów, kolorów i szumu, która przypomina nieco złożoność obrazu Marka Rothko.

Szum a design generatywny

Algorytmy szumu zostały pierwotnie zaprojektowane w celu nadania naturalnego je ne sais quoi cyfrowym teksturom. Implementacje 1D i 2D, które widzieliśmy do tej pory, były interpolacjami pomiędzy losowymi wartościami, dlatego nazywane są Value Noise, ale istnieje więcej sposobów na uzyskanie szumu...

Jak odkryłeś w poprzednich ćwiczeniach, value noise ma tendencję do wyglądania "blokowo". Aby zmniejszyć ten blokowy efekt, w 1985 roku Ken Perlin opracował inną implementację algorytmu o nazwie Gradient Noise. Ken wymyślił jak interpolować losowe gradienty zamiast wartości. Gradienty te były wynikiem funkcji losowej 2D, która zwraca kierunki (reprezentowane przez vec2) zamiast pojedynczych wartości (float). Kliknij na poniższy obrazek, aby zobaczyć kod i sposób jego działania.

Poświęć chwilę na przyjrzenie się tym dwóm przykładom autorstwa Inigo Quilez i zwróć uwagę na różnice pomiędzy value noise a gradient noise.

Podobnie jak malarz, który rozumie, jak działają pigmenty jego farb, im więcej wiemy o implementacjach szumu, tym lepiej będziemy mogli z nich korzystać. Na przykład, jeśli użyjemy dwuwymiarowej implementacji szumu do obrócenia przestrzeni, w której renderowane są linie proste, możemy uzyskać następujący drewno-podobny efekt. Ponownie możesz kliknąć na obrazek, aby zobaczyć, jak wygląda kod.

    pos = rotate2d( noise(pos) ) * pos; // obracanie przestrzeni
    pattern = lines(pos,.5); // rysowanie linii

Innym sposobem na uzyskanie ciekawych wzorów z szumu jest potraktowanie go jak pola odległości i zastosowanie niektórych sztuczek opisanych w rozdziale Kształty.

    color += smoothstep(.15,.2,noise(st*10.)); // Czarny rozprysk
    color -= smoothstep(.35,.4,noise(st*10.)); // Dziury w rozprysku

Trzecim sposobem wykorzystania funkcji szumu jest modulowanie kształtu. To również wymaga pewnych technik, które poznaliśmy w rozdziale o kształtach.

Do poćwiczenia:

• Jaki inny wzór generatywny możesz stworzyć? Co z granitem? marmurem? magmą? wodą? Znajdź trzy zdjęcia interesujących Cię tekstur i zaimplementuj je algorytmicznie za pomocą szumu.
• Użyj szumu do modulacji kształtu.
• A co z wykorzystaniem szumu do ruchu? Wróć do rozdziału Macierze. Użyj przykładu z translacją kształtu "+" i zastosuj do niego kilka losowych i szumowych ruchów.
• Zrób generatywnego Jacksona Pollocka.

Lepszy szum

Ulepszenie oryginalnego szumu Perlina, zwane Simplex Noise, polega na zastąpieniu sześciennej krzywej Hermite'a ( f(x) = 3x^2-2x^3 , która jest identyczna z funkcją smoothstep()) kwintową krzywą interpolacyjną ( f(x) = 6x^5-15x^4+10x^3 ). Dzięki temu oba końce krzywej są bardziej "płaskie", więc każda granica z wdziękiem zszywa się z następną. Innymi słowy, otrzymujesz bardziej ciągłe przejście między komórkami. Możesz to zobaczyć, odkomentowując drugą formułę w poniższym przykładzie wykresu (lub zobacz dwa równania obok siebie tutaj).

Zauważ, jak zmieniają się końce krzywej. Więcej na ten temat możesz usłyszeć z ust Kena Perlina.

Simplex Noise

Dla Kena Perlina sukces jego algorytmu nie był wystarczający. Uważał, że może on działać lepiej. Na Siggraph 2001 zaprezentował "simplex noise", w którym osiągnął następujące ulepszenia w stosunku do poprzedniego algorytmu:

• Algorytm o mniejszej złożoności obliczeniowej i mniejszej liczbie mnożeń.
• Szum, który skaluje się do wyższych wymiarów przy mniejszym koszcie obliczeniowym.
• Szum bez artefaktów kierunkowych.
• Szum z dobrze zdefiniowanymi i ciągłymi gradientami, o niskim koszcie obliczeniowym.
• Algorytm, który jest łatwy do zaimplementowania w hardware'rze.

Wiem, co myślisz... "Kim jest ten człowiek?" Tak, jego praca jest fantastyczna! Ale poważnie, w jaki sposób ulepszył ten algorytm? Cóż, widzieliśmy jak dla dwóch wymiarów interpolował 4 punkty (rogi kwadratu); możemy więc poprawnie zgadnąć, że dla trzech (zobacz implementację tutaj) i czterech wymiarów musimy interpolować 8 i 16 punktów. Prawda? Innymi słowy dla N wymiarów musisz płynnie interpolować 2 do N punktów (2^N). Ale Ken sprytnie zauważył, że chociaż oczywistym wyborem dla kształtu wypełniającego przestrzeń jest kwadrat, najprostszym kształtem w 2D jest trójkąt równoboczny. Zaczął więc od zastąpienia siatki kwadratowej (niedawno nauczyliśmy się jej używać) siatką trójkątów równobocznych (inaczej zwaną siatką sympleksową).

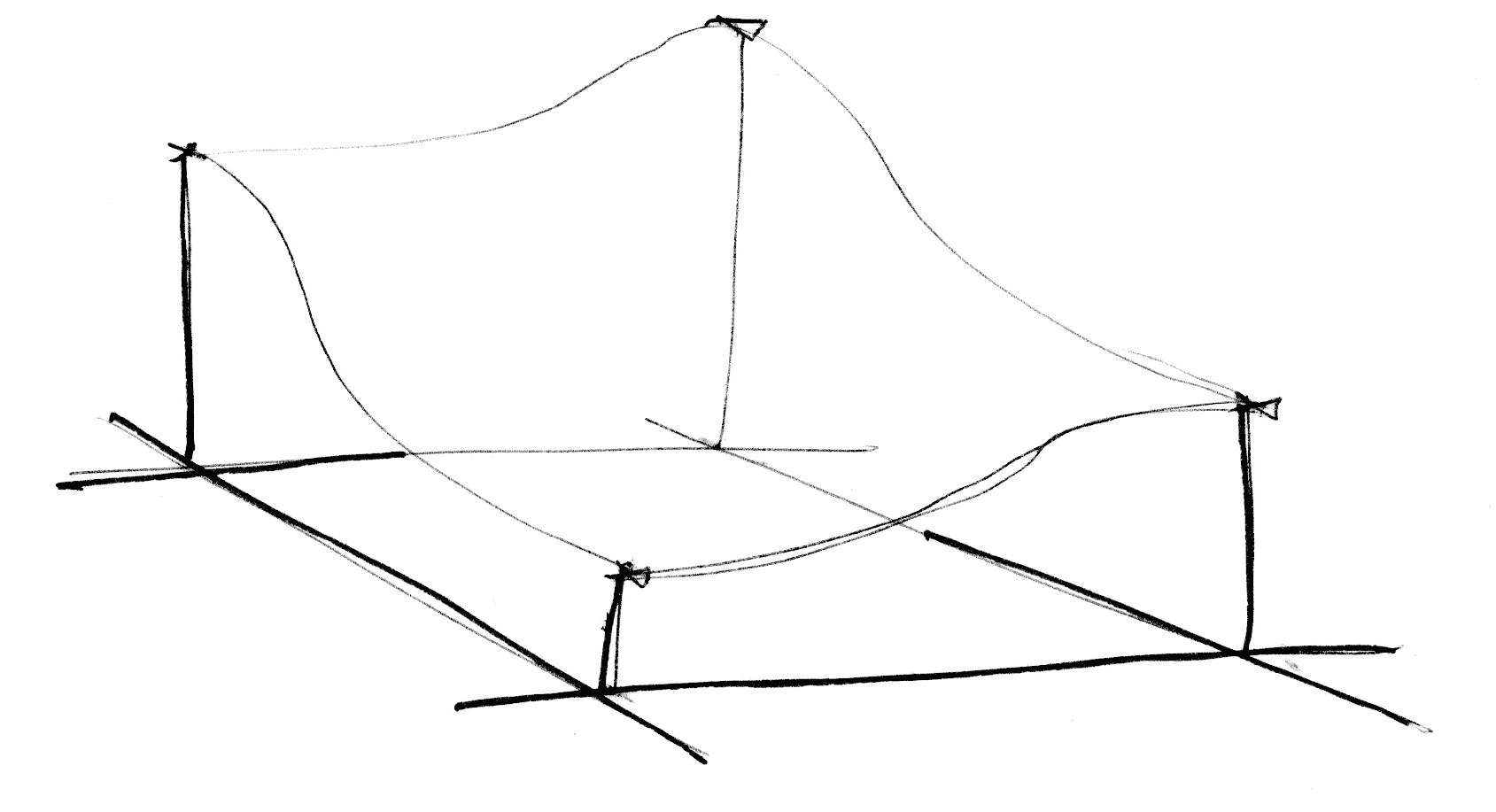
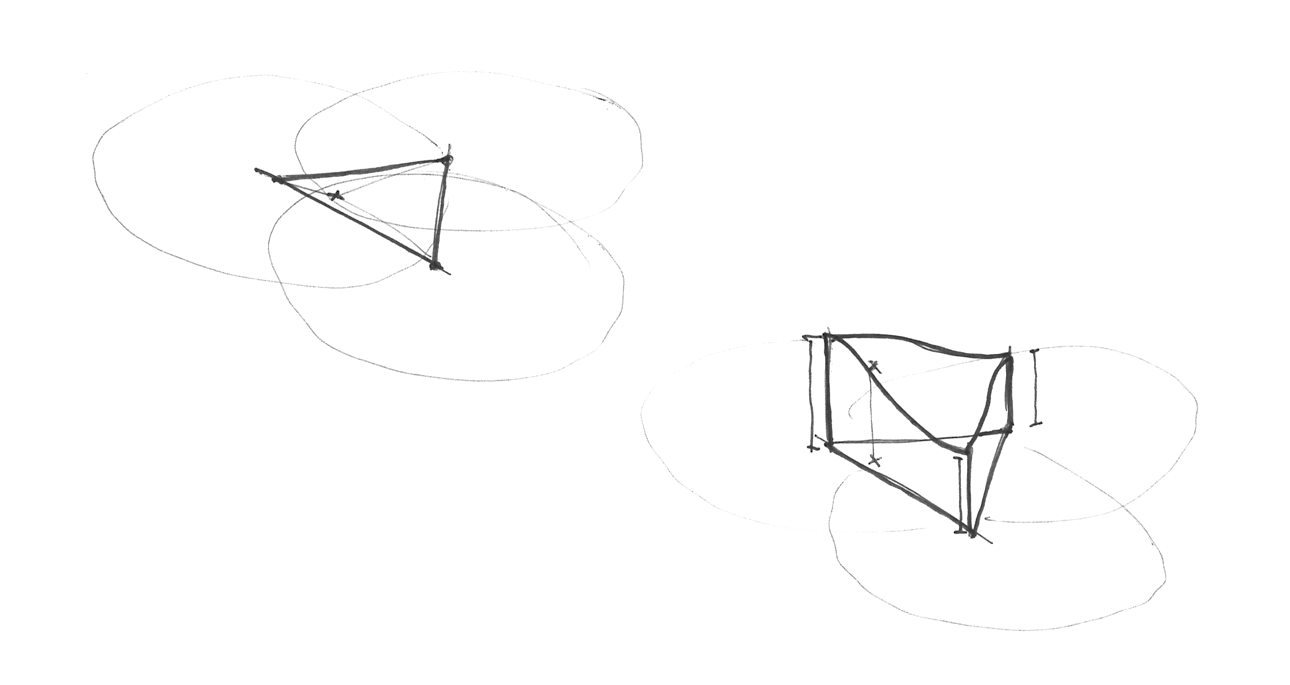
Kształt dla N wymiarów to kształt z N + 1 wierzchołkami. Innymi słowy jeden wierzchołek mniej do obliczenia w 2D, 4 wierzchołki mniej w 3D i 11 wierzchołków mniej w 4D! To ogromna poprawa!

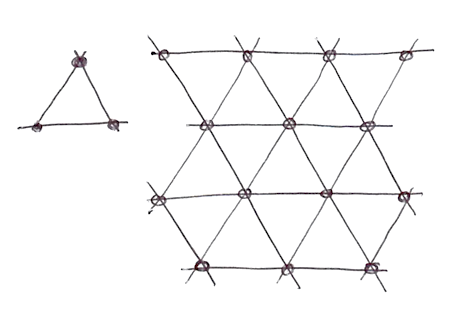
W dwóch wymiarach interpolacja odbywa się podobnie do zwykłego szumu, poprzez interpolację wartości wierzchołków odcinka. Ale w tym przypadku, dzięki zastosowaniu siatki sympleksowej, musimy tylko interpolować sumę 3 wierzchołków.

Jak powstaje siatka sympleksowa? W kolejnym błyskotliwym i eleganckim posunięciu, można ją uzyskać poprzez podział kwadratowych kafelków na dwa trójkąty równoramienne, a następnie przekrzywienia ich, aż każdy trójkąt będzie równoboczny. Proces ten szerzej opisany jest w artykule Stefana Gustavsona.

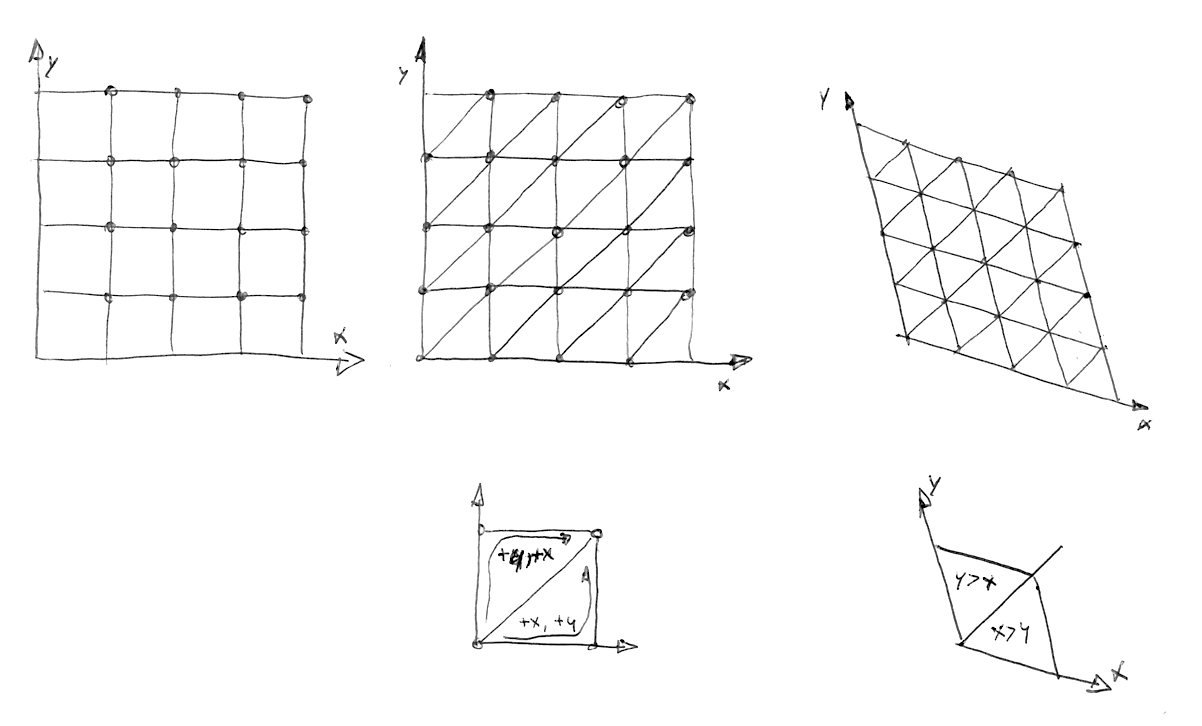
W poniższym kodzie możesz odkomentować linię 44, aby zobaczyć jak siatka jest przekrzywiona, a następnie odkomentować linię 47, aby zobaczyć siatkę simpleksową. Zauważ jak w linii 22 dzielimy przekrzywiony kwadrat na dwa trójkąty równoboczne poprzez wykrycie czy x > y (dolny" trójkąt) lub y > x (górny" trójkąt).

Wszystkie te ulepszenia skutkują algorytmicznym arcydziełem, jakim jest Simplex Noise. Poniżej znajduje się implementacja GLSL tego algorytmu wykonana przez Iana McEwana i Stefana Gustavsona (i przedstawiona w tym artykule), która w celach edukacyjnych jest nadmiernie skomplikowana , ale przekonasz się, że jest też mniej enigmatyczna niż można by się spodziewać, a kod jest krótki i szybki.

Cóż... dość technicznych rozważań, czas na wykorzystanie tego narzędzia we własny, ekspresyjny sposób:

• Kontempluj, jak wygląda każda implementacja szumu. Wyobraź sobie je jako surowy materiał, jak marmurowy kamień dla rzeźbiarza. Co możesz powiedzieć o "uczuciu", jakie ma każda z nich? Zmruż oczy, aby uruchomić wyobraźnię, tak jak wtedy, gdy chcesz znaleźć kształty w chmurze. Co widzisz? Co ci się przypomina? W co każda implementacja szumu mogłaby zostać przeobrażana? Podążając za swoją intuicją, spróbuj zrealizować to w kodzie.

• Zrób shader, który tworzy iluzję przepływu. Jak lampa lawowa, krople atramentu, woda itp.

• Użyj Simplex Noise, aby dodać trochę tekstury do pracy, którą już wykonałeś.

W tym rozdziale wprowadziliśmy pewną kontrolę nad chaosem. Nie była to łatwa praca! Zostanie zaklinaczem chaosu wymaga czasu i wysiłku.

W następnych rozdziałach zobaczymy kilka dobrze znanych technik, które pozwolą ci udoskonalić swoje umiejętności i wydobyć więcej z szumu, aby zaprojektować wysokiej jakości generatywne dzieła za pomocą shaderów. Do tego czasu ciesz się czasem na zewnątrz, kontemplując naturę i jej zawiłe wzory. Twoja umiejętność obserwacji wymaga równego (a może nawet większego) poświęcenia niż twoje umiejętności tworzenia. Wyjdź na zewnątrz i ciesz się resztą dnia!

"Talk to the tree, make friends with it." Bob Ross