Nhiễu

Sau một hồi vật lộn với các hàm ngẫu nhiên nhìn như màn hình TV hỏng, ít nhiều thì ta cũng sẽ quay cuồng và hoa mắt, giờ thì cùng nghỉ ngơi và dạo chơi tí nhé.

Ta cảm nhận được gió thổi qua da, nắng ấm rọi lên mặt. Thế giới quả là sống động. Màu sắc, họa tiết rồi cả âm thanh nữa. Hãy nhìn bề mặt của những con đường, hòn đá, ngọn cây và cả những đám mây nữa.

họa tiết khó đoán của những bề mặt này có thể coi là "ngẫu nhiên", nhưng tuyệt nhiên không giống như sự lộn xộn ở chương trước. Thế giới thực quả là rất phức tạp ! Làm sao để ta lột tả được sự đa dạng đó bằng máy tính đây ?

Đó cũng chính là câu hỏi mà Ken Perlin đã đi tìm câu trả lời suốt những năm đầu thập niên 80, khi ông chịu trách nhiệm tạo ra các họa tiết tự nhiên hết mức có thể cho bộ phim "Tron". Và kết quả là ông đã nhận được một giải Oscar với thuật toán tạo nhiễu của mình.

Đoạn code dưới đây không hẳn là thuật toán tạo nhiễu Perlin cổ điển, nhưng là một bước đệm tốt để bắt đầu.

Trông na ná như những gì ta đã làm ở chương trước. Ta tách riêng phần nguyên và phần thập phân của số thực x vào hai biến i và f bằng hai hàm floor() và fract(). Sau đó chỉ sinh số ngẫu nhiên từ phần nguyên, kết quả sẽ giống nhau cho dù bạn có chạy bao nhiêu lần đi chăng nữa.

Hai dòng cuối đã bị comment đi. Dòng đầu tiên sẽ nội suy tuyến tính 2 giá trị ngẫu nhiên ở 2 ô liên tiếp.

y = mix(rand(i), rand(i + 1.0), f);

Hãy uncomment xem đồ thị thay đổi thế nào. Tôi dùng chính phần thập phân có được từ hàm fract() và lưu trong biến f phía trên, để quyết định tỉ lệ nội suy giữa 2 số dùng hàm mix().

Nếu bạn đã đọc tới đây, hẳn là bạn đã biết chúng ta có những cách nội suy khác ngoài tuyến tính phải không ? Hãy thử uncomment dòng cuối cùng trong đoạn phía trên, tôi đã dùng hàm smoothstep() thay cho nội suy tuyến tính đó.

y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f));

Bạn sẽ thấy các đỉnh bớt nhọn hơn. Ở rất nhiều thuật toán sinh nhiễu, bạn sẽ để ý thấy các lập trình viên thường sử dụng đường cong của riêng họ (ví dụ công thức dưới đây), thay vì dùng hàm smoothstep().

float u = f * f * (3.0 - 2.0 * f ); // công thức đường cong bậc 3 với tham số riêng
y = mix(rand(i), rand(i + 1.0), u); // dùng kết quả để xác định tỉ lệ nội suy

Sự ngẫu nhiên có chuyển tiếp rất êm này thực sự là một cuộc cách mạng cho kỹ sư đồ hoạ và cả hoạ sỹ nữa - nó cho ta khả năng sinh ra các ảnh và hình khối có cảm giác hết sức tự nhiên. Thuật toán sinh nhiễu của Perlin (Perlin Noise) đã được code đi code lại trên các ngôn ngữ lập trình khác nhau để tạo nên vô vàn tác phẩm mê hoặc có tính sáng tạo cao.

Giờ tới lượt bạn:

• Hãy tự tạo một hàm float noise(float x) của riêng mình.

• Dùng chính hàm sinh nhiễu đó để di chuyển, quay hoặc thu phóng một hình vẽ.

• Kết hợp nhiều hình để xem chúng nhảy múa trên màn hình.

• Vẽ một sinh vật gì đó "trông tự nhiên".

• Khi đã có sinh vật của mình rồi, hãy thổi hồn cho nó bằng cách thêm 1 chuyển động nhé.

Nhiễu 2 chiều

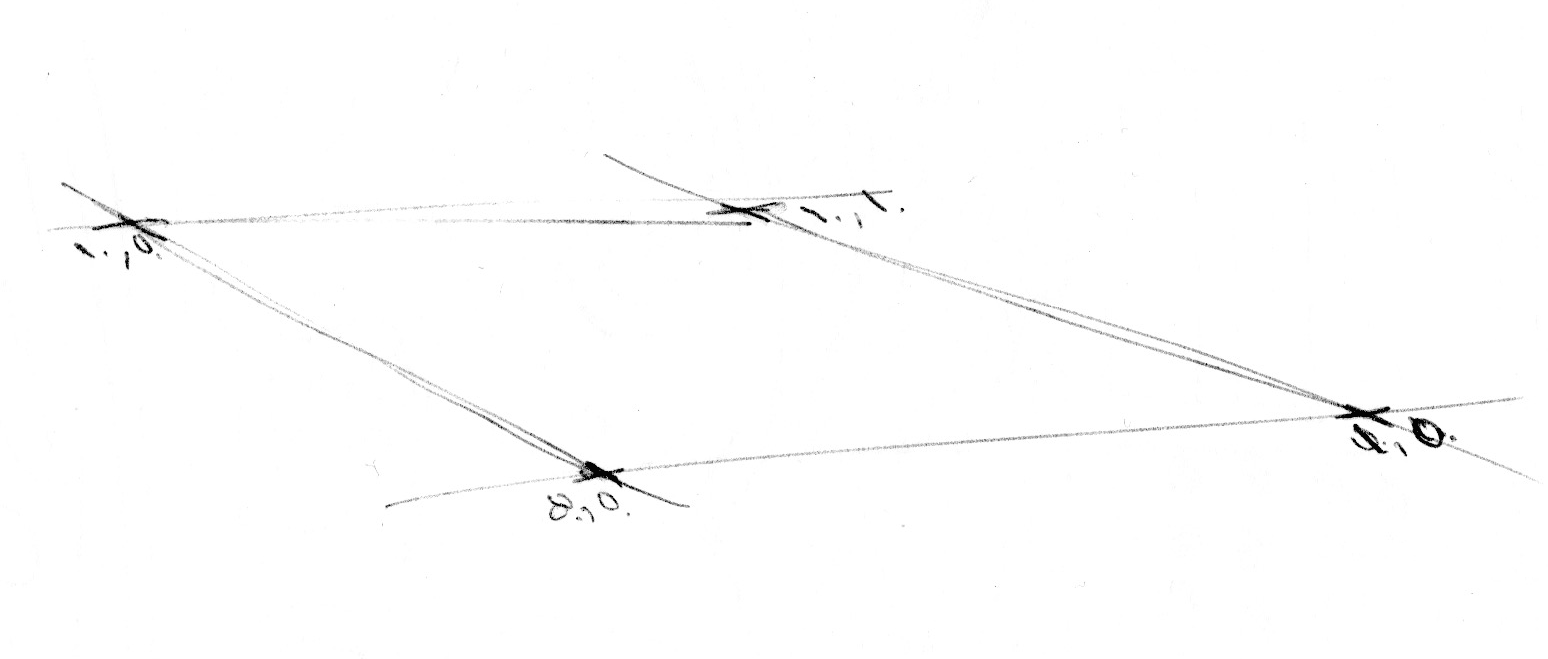
Trên đây là cách tạo nhiễu 1 chiều, giờ hãy thử 2 chiều xem sao. Thay vì nội suy giữa 2 điểm fract(x) và fract(x)+1.0, ở không gian 2 chiều, ta sẽ nội suy giữa 4 đỉnh của một tứ giác (fract(st), fract(st)+vec2(1.,0.), fract(st)+vec2(0.,1.) và fract(st)+vec2(1.,1.)).

Tương tự như vậy, nếu ta muốn sinh nhiễu 3 chiều thì sẽ phải nội suy giữa 8 đỉnh của một khối lập phương (có thể vát). Kỹ thuật này hoàn toàn dựa trên phép nội suy giữa các điểm ngẫu nhiên cố định (value), nó được gọi là value noise.

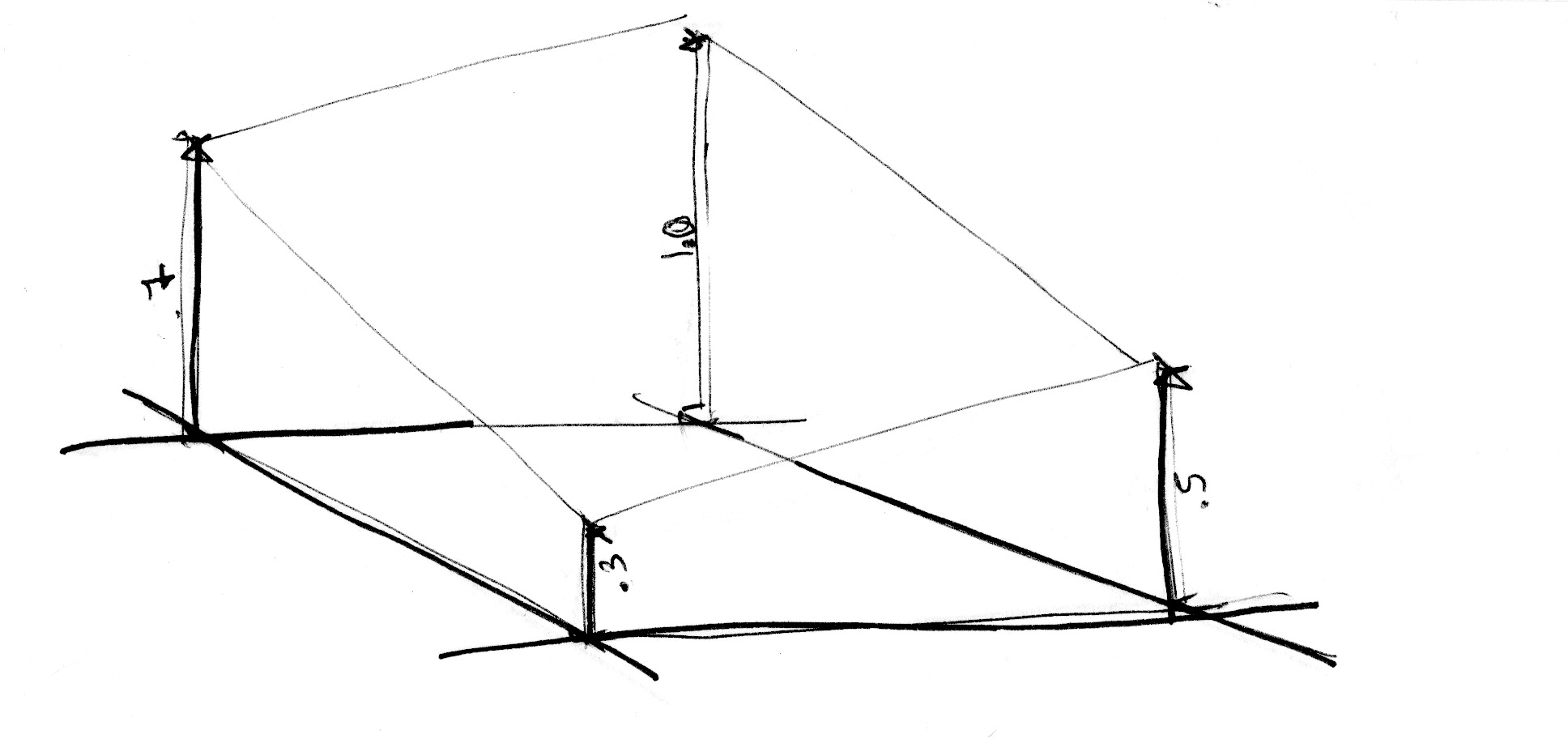
Và cũng giống như phần sinh nhiễu 1 chiều, nếu sử dụng hàm nội suy bậc 3 (cubic) thay vì tuyến tính, thì ta sẽ thu được nhiễu rất mịn.

Hãy xem hàm sinh nhiễu dưới đây:

Đầu tiên ta tạo lưới 5x5 (dòng 45) để nhìn rõ vùng chuyển tiếp giữa các ô. Trong hàm sinh nhiễu, ta xác định toạ độ của mỗi ô (số nguyên) để sinh số ngẫu nhiên đại diện cho 4 đỉnh (dòng từ 23 tới 26). Cuối cùng ở dòng 35 ta nội suy cả 4 giá trị dựa vào phần thập phân.

Giờ tới lượt bạn:

• Thử các kích thước lưới khác (dòng 45), và chuyển động nếu được

• Kích thước lớn tới đâu thì nhiễu trông giống như ngẫu nhiên

• Với kích thước nào thì không thể nhận ra nhiễu nữa

• Thử kết hợp hàm sinh nhiễu với toạ độ con trỏ chuột

• Nếu ta coi dải màu gradient sinh ra bởi nhiễu như là 1 distance field thì sao nhỉ ? Thử làm một cái gì đó hay ho với ý tưởng này xem sao.

• Giờ thì bạn kiểm soát được cả trật tự lẫn sự hỗn loạn ở một mức độ nào đó rồi, hãy thử xem bạn hiểu sâu tới đâu nhé. Hãy dùng nhiều hình chữ nhật với màu sắc khác nhau và nhiễu để mô phỏng lại bức tranh của Mark Rothko.

Ứng dụng nhiễu vào các thiết kế ngẫu nhiên

Các thuật toán sinh nhiễu ban đầu được thiết kế để thổi hồn vào các bức tranh kỹ thuật số. Các thuật toán 1 chiều và 2 chiều ta thấy trong chương này đều chỉ nội suy giữa các số ngẫu nhiên có sẵn, nên được gọi là Value Noise, nhưng còn nhiều cách khác để sinh nhiễu ...

Ở ví dụ phía trên, ta có thể thấy nhiễu sinh bởi nội suy trông như bị "vỡ ảnh". Để loại bỏ hiệu ứng này, Ken Perlin đã phát minh ra một thuật toán khác năm 1985 gọi là Gradient Noise. Ken tìm ra cách để nội suy giữa các dải màu gradient thay vì giữa các số cố định. Các dải màu này lại lại kết quả của một hàm sinh nhiễu 2 chiều khác. Click vào ảnh dưới đây để xem code của mẫu thiết kế này.

Hãy dành một chút thời gian để quan sát 2 ví dụ sau của Inigo Quilez để so sánh sự khác nhau giữa value noise và gradient noise.

Nếu một hoạ sỹ phải nắm rất rõ cách kết hợp màu trong các bức tranh, thì ta cũng phải hiểu tường tận các cách sinh nhiễu khác nhau thì mới tận dụng được. Ví dụ, nếu ta dùng nhiễu hai chiều để bẻ cong canvas đang có rất nhiều đường thẳng song song, ta có thể tạo nên vân bề mặt trông giống như gỗ vậy. Bạn có thể click vào ảnh dưới đây để xem code.

    pos = rotate2d( noise(pos) ) * pos; // xoay trục toạ độ theo nhiễu
    pattern = lines(pos,.5); // vẽ các đường thẳng

Một cách khác để tạo nên các họa tiết thú vị từ nhiễu là coi nó như 1 distance field và áp dụng các kỹ thuật được mô tả ở Chương Hình dạng.

    color += smoothstep(.15,.2,noise(st*10.)); // Các giọt bắn
    color -= smoothstep(.35,.4,noise(st*10.)); // Các vũng bắn

Cách thứ ba là dùng hàm sinh nhiễu để khiến các hình vẽ chuyển động. Để làm được thì ta cũng cần tới vài kỹ thuật được nhắc tới ở Chương Hình dạng.

Để tập luyện:

• Bạn còn có thể tạo nên các hoa văn ngẫu nhiên nào nữa ? Vân đá ? Mắc ma ? Mặt nước ? Hãy tìm ảnh của những vân bề mặt bạn thích rồi dùng thuật toán để vẽ lại.

• Dùng nhiễu để bóp méo hình vẽ.

• Dùng nhiễu để di chuyển hình vẽ. Hãy quay lại Chương Ma trận và sửa code di chuyển hình chữ thập để áp dụng thêm nhiễu nhằm tạo ra những chuyển động khó đoán hơn.

• Vẽ lại bức tranh dưới đây của Jackson Pollock.

Nhiễu cải tiến

Perlin đã tự cải tiến thuật toán sinh nhiễu ban đầu của ông để tạo ra Simplex Noise, bằng cách thay thế đường cong Hermite( f(x) = 3x^2-2x^3 , cho kết quả giống với hàm smoothstep()) bằng một đường cong bậc 5 (quintic) có công thức f(x) = 6x^5-15x^4+10x^3. Công thức nội suy này khiến cho hai đầu đường cong phẳng hơn và che được sự chuyển tiếp giữa 2 ô. Bạn có thể kiểm chứng điều đó bằng cách uncomment công thức thứ 2 ở đoạn code dưới đây (hoặc so sánh 2 phương trình cạnh nhau)

Chú ý hai đầu của đồ thị để dễ so sánh. Bạn có thể tìm hiểu thêm bằng nghiên cứu của chính Ken.

Simplex Noise

Đối với Ken Perlin thì sự thành công của thuật toán sinh nhiễu là chưa đủ, ông ấy nghĩ rằng có thể làm tốt hơn nữa. Ở hội nghị Siggraph 2001 ông đã thuyết trình thuật toán mới cải tiến hơn thuật toán cũ, gọi là "simplex noise":

• Hiệu quả hơn với ít phép tính hơn và độ phức tạp cũng thấp hơn.
• Sinh nhiễu ở các không gian nhiều chiều yêu cầu ít dữ liệu hơn thuật toán cũ.
• Các điểm ảnh dọc theo trục toạ độ không còn bị lộ nữa (vì quá gần với các điểm nội suy nên thường có giá trị tương đương)
• Các dải màu gradient dùng để sinh nhiễu có thể được tính rất nhanh và dễ kiểm soát
• Phần cứng có thể hỗ trợ để tối ưu thuật toán này dễ dàng

Tôi biết bạn đang tự hỏi ... "Đây là cao nhân phương nào?" Đúng vậy, các sản phẩm của ông thật siêu đẳng! Nhưng nói một cách nghiêm túc thì ông tự cải tiến thuật toán bằng cách nào ? Đầu tiên ông ấy quan sát cách sinh nhiễu ở không gian 2 chiều và thấy cần dùng 4 đỉnh, ở không gian 3 chiều sẽ cần 8 đỉnh và 4 chiều thì cần 16 đỉnh. Vậy là để sinh nhiễu ở không gian N chiều thì ta sẽ cần 2^N đỉnh. Và Ken đã nhanh chóng nhận ra rằng một tứ giác 4 đỉnh đâu phải hình học đơn giản nhất ở không gian 2 chiều đâu, đó phải là hình tam giác mới đúng. Và nếu muốn lấp đầy không gian bằng một lưới các tam giác thì tam giác đều sẽ giúp việc code đơn giản hơn. Ý tưởng cải tiến chỉ có vậy.

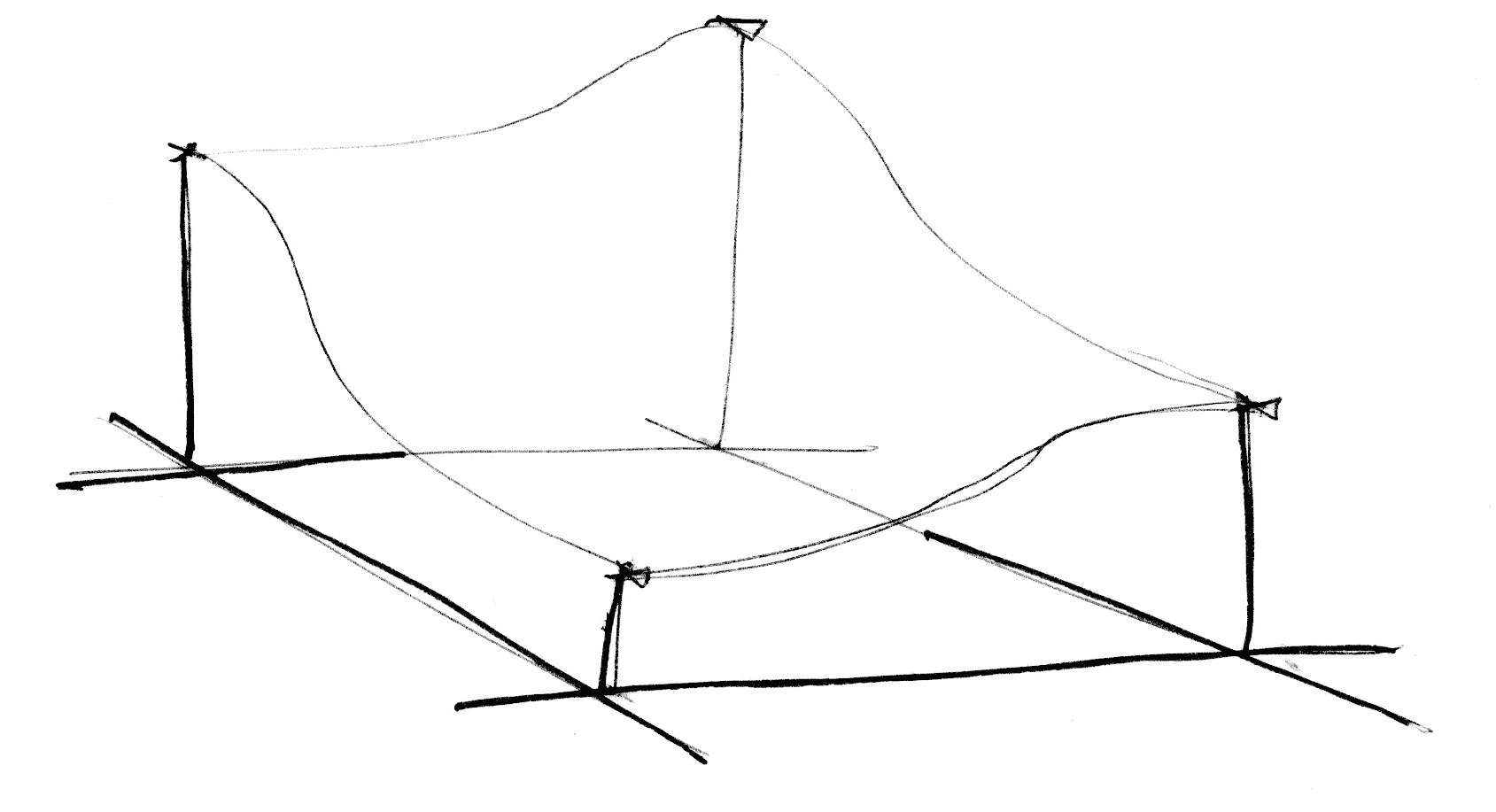
Và để sinh nhiễu cho không gian N chiều, ta sẽ chỉ cần N + 1 đỉnh. So với thuật toán cũ, thuật toán mới này giúp ta tiết kiệm 1 đỉnh ở không gian 2 chiều, 4 đỉnh ở không gian 3 chiều và 11 đỉnh ở không gian 4 chiều! Số lượng phép tính được cắt bớt cực kỳ nhiều. Quả là một cải tiến vượt bậc.

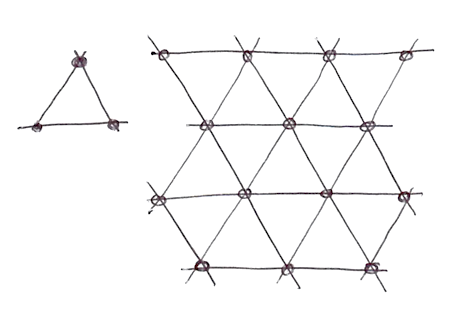
Lúc này, để tính toán giá trị nhiễu tại một điểm ảnh, ta chỉ cần mix giá trị ngẫu nhiên tại 3 đỉnh.

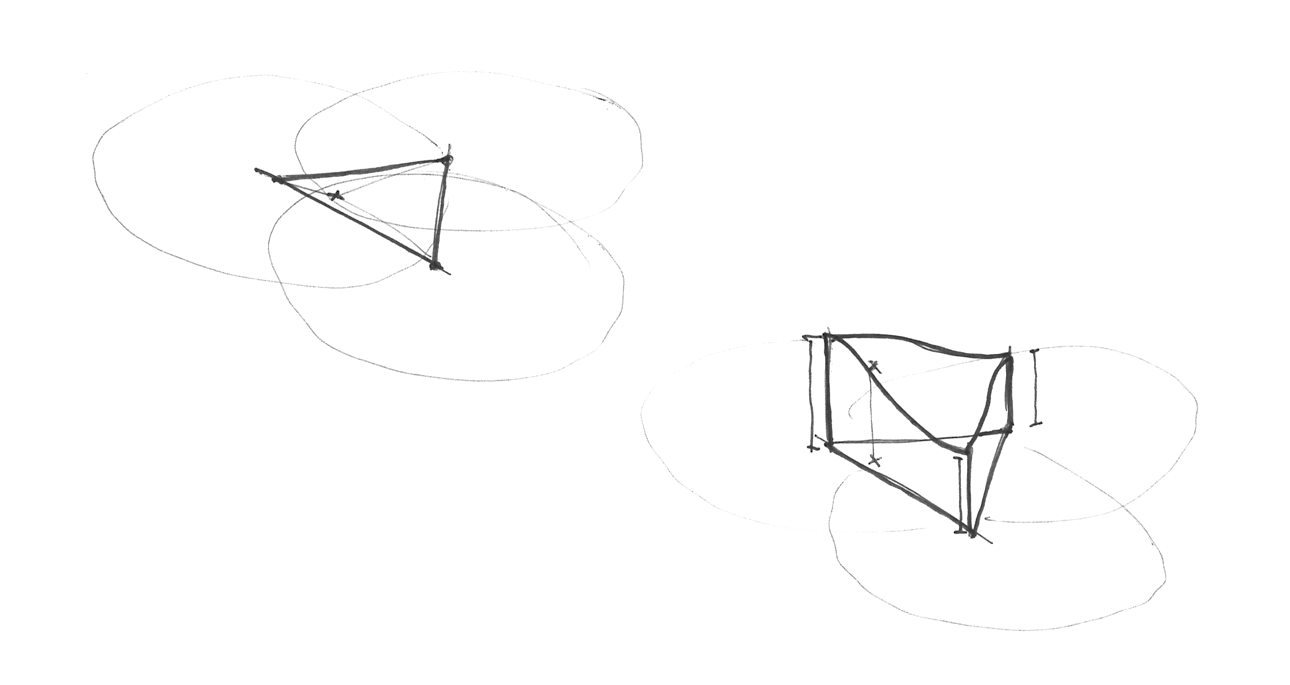
Vậy để tạo ra lưới tam giác (simplex grid) này thì làm thế nào ? Lại thêm một nước đi sáng suốt và tinh tế nữa, chỉ bằng cách chia đôi mỗi ô vuông ở lưới dạng bảng thông thường thành 2 nửa tam giác, rồi xô nghiêng (skew) cả lưới tới khi 3 cạnh của mỗi tam giác bằng nhau là được.

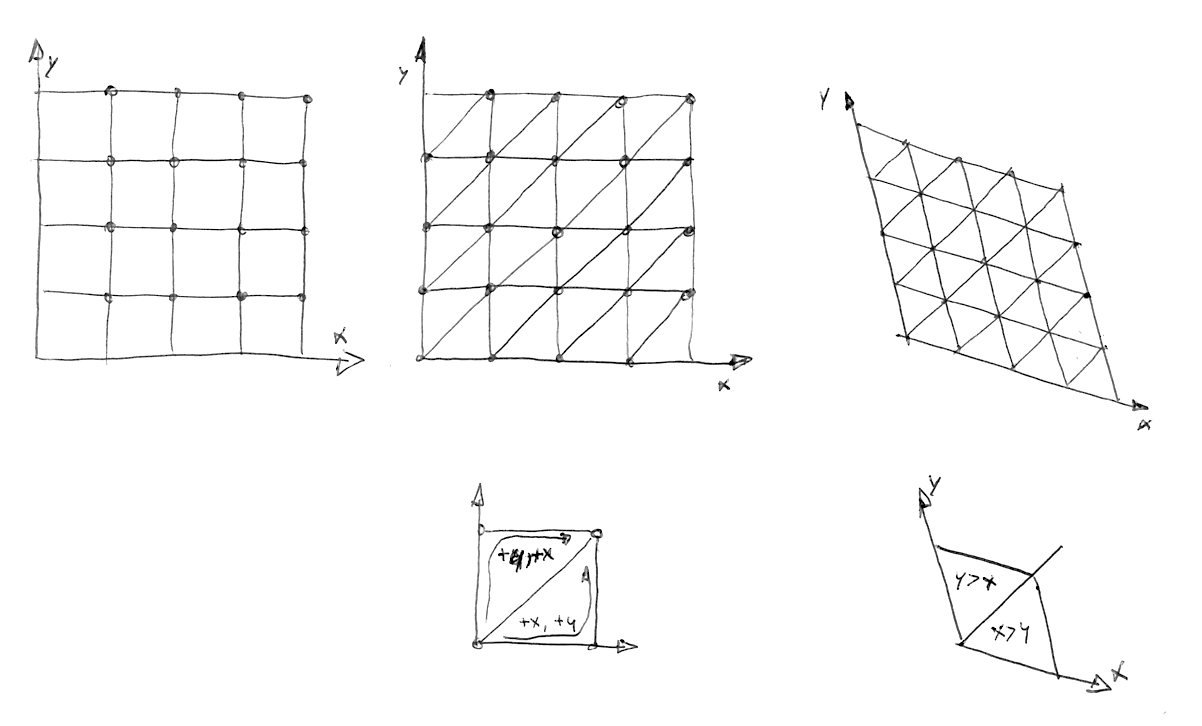
Stefan Gustavson đã mô tả thuật toán này trong báo cáo của ông như sau:

"...chỉ cần kiểm tra phần nguyên trong toạ độ (x,y) của điểm ảnh ta cần tô màu, ta có thể nhanh chóng xác định nó ở ô vuông nào trong lưới dạng bảng. Rồi cũng chỉ cần so sánh x với y là ta biết được điểm ảnh nằm ở tam giác nào trong ô vuông đó, cuối cùng chỉ cần nội suy giá trị giữa 3 đỉnh tam giác là xong."

Trong đoạn code dưới đây, bạn có thể uncomment dòng 44 để thấy lưới vuông bị xô nghiêng như thế nào, và uncomment tiếp dòng 47 để thấy một lưới tam giác được hình thành. Ở dòng 22, chỉ với một phép so sánh đơn giản x > y, ta có thể xác định được điểm ảnh nằm ở tam giác nào trong số 2 tam giác tạo thành mỗi ô vuông.

Các cải tiến này đã góp phần tạo nên một thuật toán kiệt tác gọi là Simplex Noise. Hình vẽ dưới đây được tạo bởi chính thuật toán này trong GLSL bởi Ian McEwan và Stefan Gustavson (và được mô tả trong báo cáo này) với một mức độ phức tạp quá tầm với một dự án giáo dục như thế này, nhưng nếu bạn click vào hình thì sẽ thấy ngạc nhiên là code rất ngắn gọn và tối ưu.

Chà... lý thuyết thế đủ rồi nhỉ, giờ hãy xắn tay áo lên nào:

• Hãy chiêm ngưỡng các vân bề mặt tuyệt đẹp của thiên nhiên và nghĩ xem có thể dùng thuật toán sinh nhiễu nào để mô phỏng không. Nếu cần thì cứ nheo mắt lại mà tưởng tượng như lúc đoán xem các đám mây có hình gì ấy.

• Tạo shader mô phỏng một dòng chảy, như dòng dung nham, giọt mực, dòng nước ...

• Sử dụng Simplex Noise để thêm vân bề mặt vào một hình vẽ nào đó bạn đã tạo ra.

Ở chương này chúng tôi đã giới thiệu một vài kỹ thuật giúp kiểm soát sự hỗn loạn. Không dễ chút nào! Để trở thành một noise-bender thành thạo tốn rất nhiều thời gian và công sức.

Ở các chương tiếp theo ta sẽ thấy một vài kỹ thuật nổi tiếng khác giúp bạn hoàn thiện bộ kỹ năng của mình để bắt đầu thiết kế ra những tác phẩm có chất lượng cao bằng shader. Cho tới lúc đó, hãy tận hưởng thiên nhiên và cố gắng tìm ra các họa tiết ẩn giấu từ Mẹ Trái Đất nhé. Kỹ năng quan sát của bạn ít ra cũng phải tương đồng với kỹ năng chế tác. Hãy thư giãn nhé!

"Hãy làm bạn và nói chuyện với cái cây" - Bob Ross