Клітинний шум

У 1996 році, через шістнадцять років після оригінального шуму Перліна та за п’ять років до його симплексного шуму, Steven Worley написав статтю під назвою “Базова функція клітинної текстури”. У ній він описує техніку процедурного текстурування, яка зараз широко використовується графічною спільнотою.

Щоб зрозуміти принципи, що лежать в її основі, нам потрібно почати думати в термінах ітерацій. Напевно, ви розумієте, що це означає використання циклів for. У циклах for в GLSL є лише одна заковика: число, яке використовується у перевірці лічильника, має бути константою (const). Отже, ніяких динамічних циклів — кількість ітерацій має бути фіксованою.

Давайте розглянемо приклад.

Точки у полі відстаней

Клітинний шум базується на полях відстаней, що розташовані до найближчої точки з певного набору. Скажімо, ми хочемо створити поле відстаней з 4 точок. Що нам потрібно зробити? Для кожного пікселя ми хочемо обчислити відстань до найближчої точки. Це означає, що нам потрібно виконати ітерацію по всім точкам, обчислити до них відстані від поточного пікселя та зберегти значення до найближчої.

    float min_dist = 100.; // змінна для збереження відстані до найближчої точки

    min_dist = min(min_dist, distance(st, point_a));
    min_dist = min(min_dist, distance(st, point_b));
    min_dist = min(min_dist, distance(st, point_c));
    min_dist = min(min_dist, distance(st, point_d));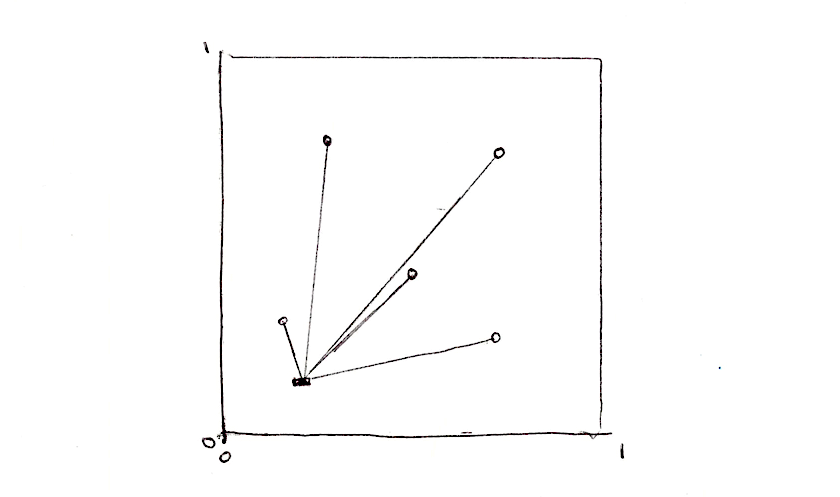

Не дуже елегантно, але робить свою справу. Тепер реалізуємо цей підхід за допомогою масиву та циклу for:

    float m_dist = 100.;  // мінімальна відстань

    for (int i = 0; i < TOTAL_POINTS; i++) {
        float dist = distance(st, points[i]);
        m_dist = min(m_dist, dist);
    }

Зверніть увагу, як ми використовуємо цикл for, щоб перебирати масив точок і відстежувати мінімальну відстань за допомогою функції min(). Ось коротка робоча реалізація цієї ідеї:

У наведеному вище коді одна з точок прив'язана до положення курсору. Пограйте з прикладом, щоб отримати краще інтуїтивне уявлення щодо поведінки програми. Потім спробуйте наступне:

• Як анімувати решту точок?
• Прочитавши розділ про фігури, уявіть цікаві способи використання з цим полем відстаней!
• Як додати більше точок до цього поля відстаней? Що можна зробити для динамічного додавання або видалення точок?

Замощення та ітерація

Ви, мабуть, помітили, що цикли for та масиви не дуже дружать з GLSL. Як ми вже говорили раніше, місцеві цикли не здатні на динамічну кількість ітерацій. Крім того, велика кількість ітерацій значно знижує продуктивність вашого шейдера. Це означає, що ми не можемо використовувати цей прямолінійний підхід для великої кількості точок. Нам потрібно знайти іншу стратегію, яка буде використовувати переваги архітектури GPU з її паралельними обчисленнями.

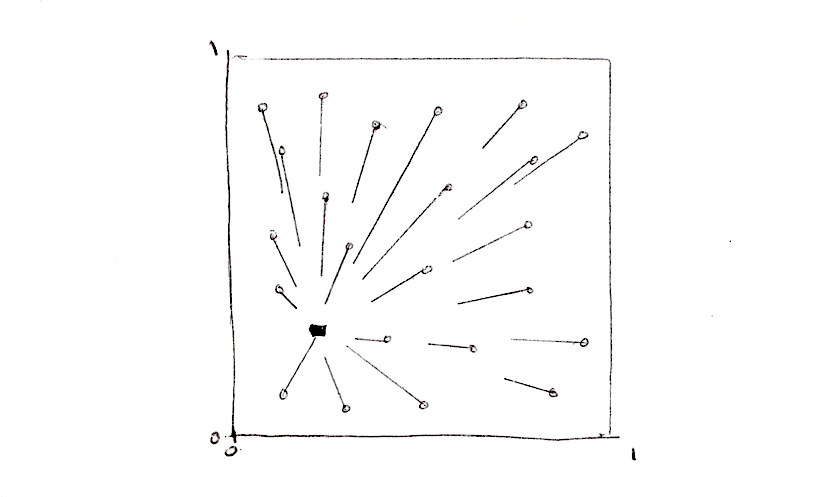
Один з підходів до розв'язання цієї проблеми — це розділення простору на плитки. Кожному пікселю не обов'язково перевіряти відстань до кожної окремої точки, чи не так? Враховуючи той факт, що кожен піксель працює у власному потоці, ми можемо розділити простір на комірки, кожна з яких матиме одну унікальну точку для спостереження. Крім того, щоб уникнути аберацій на межах між комірками, нам потрібно перевірити відстань до точок лише у сусідніх клітинах. Це і є головною чудовою ідеєю у статті Steven Worley. Зрештою, кожен піксель має перевірити лише дев’ять позицій: точку своєї клітини та точки у 8 клітинах навколо неї. Ми вже поділяли простір на комірки в розділах про: патерни, випадковість та шум, тож, сподіваюся, ви вже знайомі з цією технікою.

    // Масштаб
    st *= 3.;

    // Розділ простору на плитки
    vec2 i_st = floor(st);
    vec2 f_st = fract(st);

Отже, який план? Ми будемо використовувати координати клітини-плитки, збережені в цілочисельній координаті i_st, щоб побудувати випадкову позицію точки. Функція random2f, яку ми будемо використовувати, отримує на вхід vec2 та повертає нам також vec2 з випадковою для даної клітини координатою. Таким чином, для кожної плитки ми матимемо одну особливу точку у випадковому місці цієї плитки.

    vec2 point = random2(i_st);

Кожен піксель усередині плитки, з координатою збереженою у змінній f_st, перевірятиме свою відстань до випадкової точки, про яку ми говорили раніше.

    vec2 diff = point - f_st;
    float dist = length(diff);

Результат буде виглядати так:

Нам все ще потрібно перевірити відстані до точок у навколишніх клітинах, а не лише на поточній. Для цього нам потрібно ітерувати сусідні клітини. Не всі клітини, а лише ті, що знаходяться безпосередньо навколо поточної. Тобто від -1 клітини ліворуч, до +1 клітини праворуч по осі x та від -1 клітини знизу до +1 клітини зверху по осі y. Цю ділянку розміром 3x3 із 9 клітин можна обійти за допомогою подвійного циклу for:

for (int y= -1; y <= 1; y++) {
    for (int x= -1; x <= 1; x++) {
        // Сусідня позиція клітини у сітці
        vec2 neighbor = vec2(float(x), float(y));
        ...
    }
}

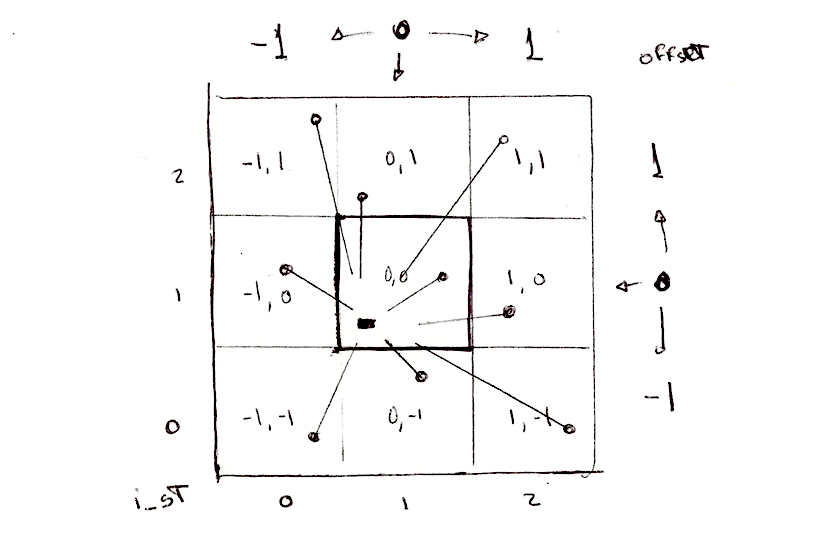
Тепер у вкладеному циклі for ми можемо обчислити положення наших випадкових точок у кожній сусідній клітині, додаючи зміщення сусідньої клітини до координат поточної.

        ...
        // Положення випадкової точки у сусідній плитці
        vec2 point = random2(i_st + neighbor);
        ...

Решта зводиться до обчислення відстаней до цієї точки та збереження найближчої у змінну m_dist.

        ...
        vec2 diff = neighbor + point - f_st;

        // Відстань до точки
        float dist = length(diff);

        // Збереження ближчої дистанції
        m_dist = min(m_dist, dist);
        ...

Наведений вище код створено на основі статті Inigo's Quilez, де він писав:

"... варто зазначити, що у наведеному вище коді є гарний трюк. Більшість реалізацій страждають від проблем із точністю, оскільки вони генерують свої випадкові точки в просторі "домену" (наприклад, у "глобальному" просторі чи просторі "об'єкта"), який може бути як завгодно далеко від початку координат. Проблему можна вирішити, перемістивши весь код до типів даних з вищою точністю, або проявивши трохи кмітливості. Моя реалізація генерує точки не в просторі "домену", а в просторі "комірки": як тільки із фрагментного пікселя отримано цілу та дробову частини, а значить визначено клітину, в якій ми працюємо, нас цікавитиме лише те, що відбувається навколо цієї клітини, а не весь простір. Тобто ми можемо відкинути цілочисельну частину значення наших координат та зберегти кілька біт точності. Насправді у звичайній реалізації діаграми Вороного, цілі частини координат точки просто скасовуються, коли випадкові точки клітини віднімаються від поточної шейдерної точки. У реалізації вище ми не робимо цього, оскільки переносимо всі обчислення в простір "комірки". Цей підхід дозволяє накласти діаграму Вороного хоч на цілу планету — достатньо просто подвоїти точність для вхідних даних, виконати для них обчислення з floor() і fract(), а решту обчислень проводити вже зі звичайною точністю для float, не витрачаючи обчислювальні ресурси на зміну всієї реалізації до подвійної точності. Звісно, той самий трюк можна застосувати й до підходів з шумом Перліна, але я ніколи не бачив подібну реалізацію чи опис подібного алгоритму)."

Підсумовуючи: розбиваємо простір на клітини. Кожен піксель обчислює відстань до точки у власній клітині та навколишніх 8 клітинах, зберігаючи найближчу відстань. В результаті маємо поле відстаней, що виглядає як на прикладі нижче:

Дослідіть цей приклад глибше:

• Масштабуйте простір різними значеннями.
• Вигадайте інші способи анімації точок.
• Що потрібно зробити для обчислення додаткової точки у положенні курсору?
• Які інші способи побудови цього поля відстаней ви можете собі уявити, окрім m_dist = min(m_dist, dist);?
• Які цікаві візерунки можна зробити за допомогою цього поля відстаней?

Цей алгоритм також можна інтерпретувати з точки зору точок, а не пікселів. У цьому випадку його можна описати таким чином: кожна точка росте, доки не натрапить на область росту іншої точки. Ця поведінка відображає деякі правила росту в природі. Живі організми формуються через цю напругу між внутрішньою силою зростання й розширення та обмеженнями зовнішніх сил. Класичний алгоритм, який імітує таку поведінку, названий на честь Георгія Вороного.

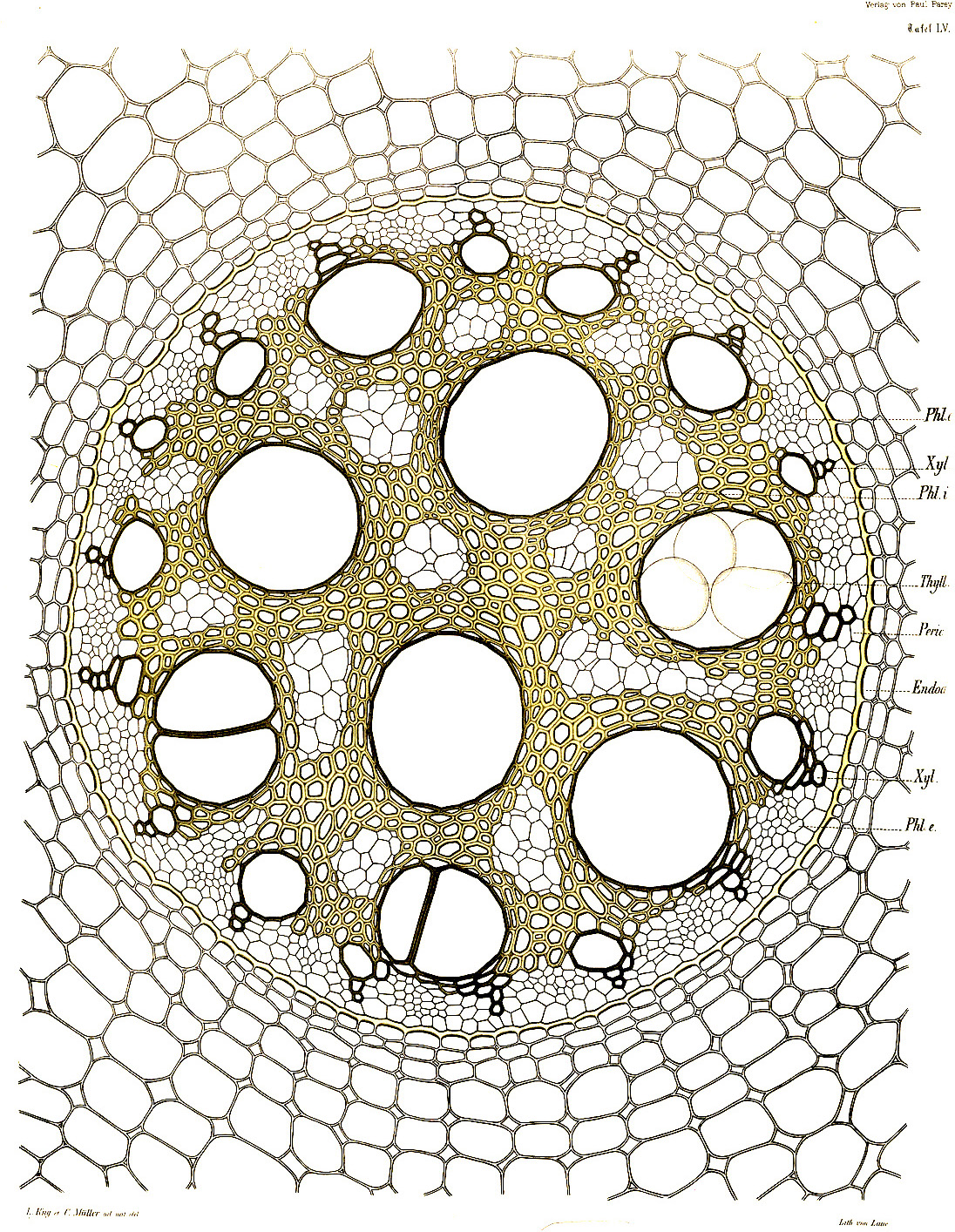
Алгоритм Вороного

Побудувати діаграми Вороного з клітинного шуму не так складно, як може здатися. Нам просто потрібно зберегти додаткову інформацію про найближчу точку до пікселя. Для цього ми використаємо змінну m_point типу vec2. Зберігаючи вектор напрямку до найближчої точки замість відстані, ми "отримаємо" "унікальний" ідентифікатор цієї точки.

    ...
    if ( dist < m_dist ) {
        m_dist = dist;
        m_point = point;
    }
    ...

Зауважте, що в наступному коді, для обчислення найближчої відстані ми використовуємо звичайний оператор if замість функції min. Чому? Тому що, при знаходженні нової найближчої точки, ми хочемо зробити додаткову дію і зберегти її координати (рядки 32-37).

Зверніть увагу, як колір рухомої комірки, прив'язаної до положення курсору, змінює колір відповідно до його положення. Це тому, що колір визначається залежно від позиції найближчої точки.

Як і у попередніх прикладах, настав час збільшити масштаби, скориставшись підходом зі статті за авторства Steven Worley. Спробуйте реалізувати його самостійно. Ви можете скористатися допомогою наступного прикладу, клацнувши на нього. Зауважте, що оригінальний підхід від Steven Worley використовує змінну кількість точок для кожної клітини, більш ніж одну у більшості випадків. У його програмній реалізації на мові C це використовується для прискорення циклу завдяки раннім виходам із нього. Цикли GLSL не дозволяють змінювати кількість ітерацій, тому вам, ймовірно, доведеться використовувати лише одну точку на клітину.

Розібравшись із цим алгоритмом, подумайте про цікаві та креативні способи його використання.

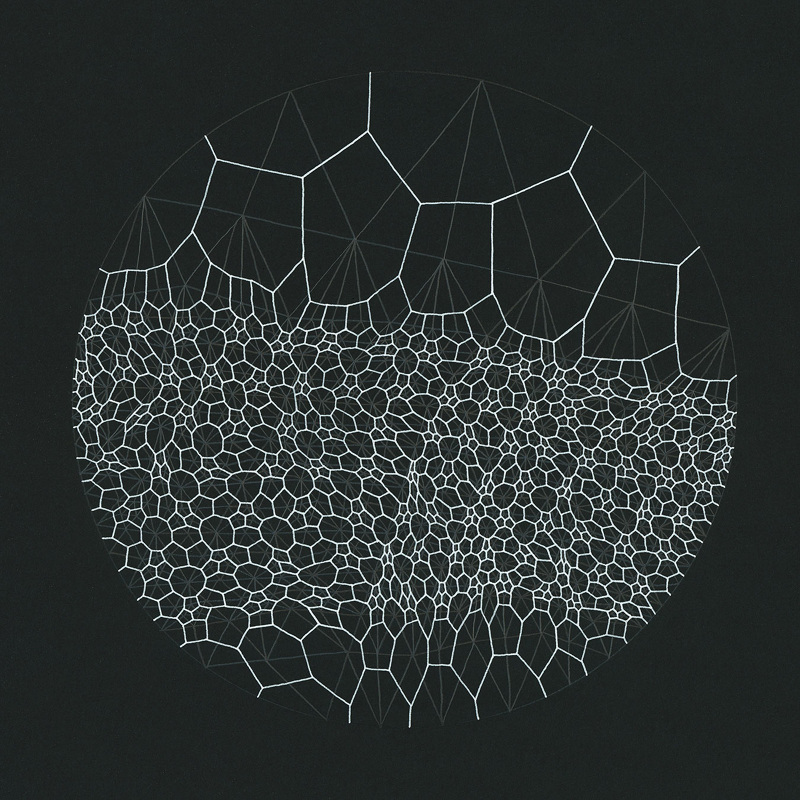
Поліпшення діаграми Вороного

У 2011 році Stefan Gustavson оптимізував алгоритм Steven Worley для GPU, обходячи лише матрицю 2x2 замість 3x3. Це значно зменшує обсяг роботи, але може створювати артефакти у вигляді розривів на краях між клітинами. Подивіться на наступні приклади:

Пізніше у 2012 році Inigo Quilez написав статтю про створення точних меж для комірок Вороного.

На цьому експерименти Inigo з Вороним не закінчилися. У 2014 році він написав чудову статтю про функцію voro-noise, яка дозволяє поступово змішувати звичайний шум з комірками Вороного. Ось вирізка з його слів:

"Попри схожість, сітка в обох патернах використовується по різному. Шум інтерполює/усереднює випадкові значення (як у шумі значення) або градієнти (як у градієнтному шумі), тоді як алгоритм Вороного обчислює відстань до найближчої опорної точки. Плавна білінійна інтерполяція та обчислення мінімума — дві дуже різні операції чи... ні? Чи можна їх об’єднати у більш загальну метрику? Якщо так, то шум та патерни Вороного можна розглядати як окремі випадки більш загального генератора патернів на основі регулярної сітки?»

Настав час придивитися до навколишніх речей, надихнутися природою, знайти власну ідею та спробувати сили у цій техніці!