Nhiễu mô phỏng tế bào (Cellular noise)
Vào năm 1996, mười sáu năm sau khi thuật toán sinh nhiễu đầu tiên của Perlin được công bố, và năm năm sau khi Thế giới biết đến thuật toán Simplex Noise của ông, Steven Worley đã viết một báo cáo khoa học với tên gọi "Vân bề mặt mô phỏng tế bào" (A Cellular Texture Basis Function). Trong nghiên cứu của mình, ông ấy đã mô tả một kỹ thuật sinh vân bề mặt mà giờ đây được sử dụng rộng khắp bởi cộng đồng đồ hoạ.
Để hiểu được các nguyên lý đằng sau, ta cần tư duy theo kiểu duyệt (iteration). Có thể bạn nghe thấy quen quen, đúng, ta đã suy nghĩ tương tự khi sử dụng vòng lặp for rồi. Có một hạn chế về vòng lặp for trong GLSL, đó là: số vòng lặp phải cố định.
Hãy cùng nhìn một ví dụ.
Các điểm trong một distance field
Nhiễu mô phỏng tế bào (Cellular noise) dựa trên distance field, khoảng cách tới một trong số những đỉnh gần nhất. Giả sử ta muốn tạo một distance field có 4 đỉnh. Ta phải làm gì ? Với mỗi điểm ảnh, tính khoảng cách tới đỉnh gần nhất. Điều đó có nghĩa là ta cần phải duyệt qua tất cả các đỉnh, tính khoảng cách từ điểm ảnh tới từng đỉnh một và lưu lại khoảng cách gần nhất.
float min_dist = 100.; // Biến lưu lại khoảng cách gần nhất
min_dist = min(min_dist, distance(st, point_a));
min_dist = min(min_dist, distance(st, point_b));
min_dist = min(min_dist, distance(st, point_c));
min_dist = min(min_dist, distance(st, point_d));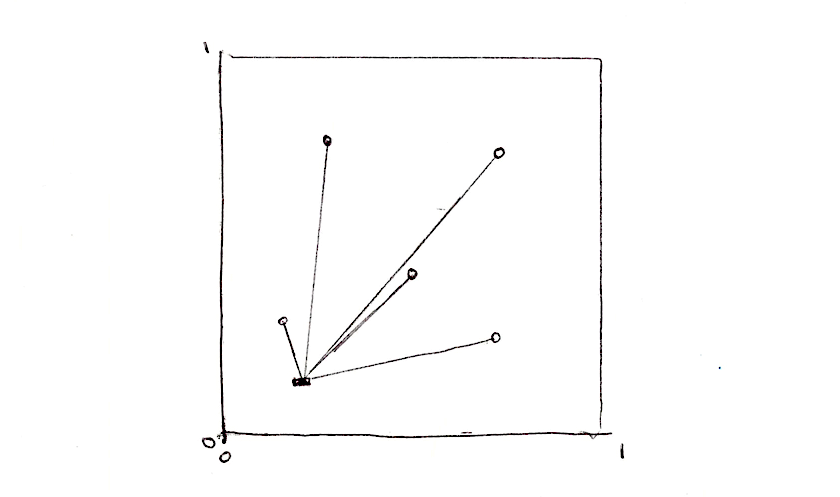
Nhìn thì không tinh tế lắm nhưng được việc. Giờ hãy chuyển đoạn code kia thành một vòng lặp nhé.
float m_dist = 100.; // khoảng cách nhỏ nhất
for (int i = 0; i < TOTAL_POINTS; i++) {
float dist = distance(st, points[i]);
m_dist = min(m_dist, dist);
}Chú ý cách tôi dùng vòng lặp for để duyệt qua mảng chứa vị trí từng đỉnh, và lưu lại khoảng cách nhỏ nhất bằng hàm min(). Đoạn code dưới đây làm đúng như vậy:
Trong đoạn code phía trên, một trong các đỉnh là vị trí của con trỏ chuột. Di chuyển con trỏ chuột để có minh hoạ trực quan về thuật toán này nhé. Sau đó hãy thử nghĩ:
- Làm sao để di chuyển các đỉnh còn lại ?
- Sau khi đọc Chương hình dạng, hãy nghĩ ra các cách khác để sử dụng distance field
- Nếu muốn thêm nhiều đỉnh hơn thì làm thế nào ? Nếu muốn tự do thêm bớt đỉnh thì sao ?
Vòng lặp duyệt các phần tử
Bạn có thể đã nhận ra vòng lặp for và mảng không phải là bạn tốt của GLSL. Như tôi đã nói trước đó, vòng lặp yêu cầu cố định số vòng lặp ngay từ đầu. Ngoài ra thì việc duyệt từng phần tử cũng khiến code shader chậm hơn đáng kể. Điều đó có nghĩa là nếu có nhiều đỉnh ta không thể dùng cách này. Ta phải tìm một chiến thuật khác, sao cho tận dụng được ưu thế về kiến trúc tính toán song song của GPU.
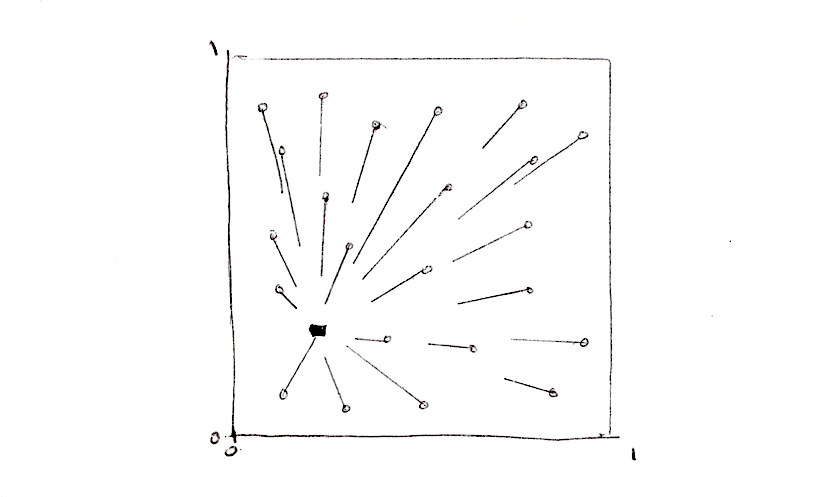
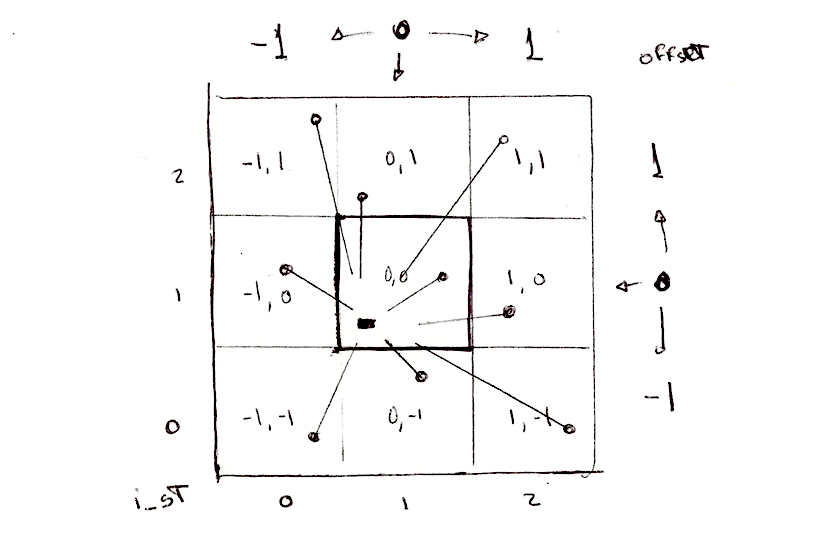
Một giải pháp được đưa ra là chia nhỏ không gian thành nhiều phần. Đâu nhất thiết phải tính khoảng cách của từng điểm ảnh với tất cả các đỉnh, phải không ? Giả sử mỗi điểm ảnh được xử lý trên một thread riêng, ta có thể chia canvas thành nhiều ô, mỗi ô chỉ có 1 đỉnh trong đó, gọi là nhân. Để tránh lỗi ở phần biên giới giữa các ô, ta sẽ cần tính khoảng cách của các pixel trong mỗi ô với nhân của các ô lân cận nữa. Đó chính là ý tưởng chủ đạo trong nghiên cứu của Steven Worley. Tóm lại, mỗi điểm ảnh chỉ cần tính khoảng cách với tối đa 9 nhân: 1 nhân ở cùng ô với điểm ảnh, và 8 nhân ở các ô xung quanh. Ta cũng đã biết cách chia nhỏ canvas thành nhiều ô ở các chương trước khi bàn về: Mẫu họa tiết, Sự ngẫu nhiên và Nhiễu, nên tôi hy vọng bạn đã thuần thục kỹ năng này rồi.
// Phóng to
st *= 3.;
// Chia nhỏ
vec2 i_st = floor(st);
vec2 f_st = fract(st);Vậy, kế hoạch là gì ? Ta sẽ dùng toạ độ hàng cột (phần nguyên) của mỗi ô (lưu trong i_st) để sinh một cặp số ngẫu nhiên, chính là vị trí của nhân trong ô đó. Hàm random2
nhận một vec2 và trả về một vec2 gồm 2 số ngẫu nhiên, chính là để thực hiện việc sinh ra một nhân có vị trí ngẫu nhiên trong ô này.
vec2 point = random2(i_st);Mỗi điểm ảnh trong ô này sẽ tính khoảng cách từ toạ độ của chính nó (lưu trong f_st) với nhân.
vec2 diff = point - f_st;
float dist = length(diff);Kết quả thu được như sau:
Ta sẽ cần tính thêm khoảng cách tới nhân của các ô xung quanh nữa. Để làm được việc đó, ta cần duyệt qua các ô xung quanh, tức là các ô nằm trong phạm vi 3x3 có toạ độ X và Y trong khoảng [-1, 1] so với ô hiện tại. Ta có thể dùng 2 vòng lặp for lồng nhau để làm việc đó:
for (int y= -1; y <= 1; y++) {
for (int x= -1; x <= 1; x++) {
// Các ô liền kề trong lưới
vec2 neighbor = vec2(float(x),float(y));
...
}
}
Hãy nhớ rằng các hàm ngẫu nhiên không thật sự ngẫu nhiên, vì thế ta có thể biết vị trí của nhân ở một ô bất kỳ bằng cách gọi lại hàm random2 với tham số giống như ở chính ô đó vậy.
...
// Tính vị trí nhân ở ô liền kề
vec2 point = random2(i_st + neighbor);
...Phần còn lại chỉ là tính khoảng cách với các nhân và lưu lại khoảng cách nhỏ nhất vào biến m_dist.
...
vec2 diff = neighbor + point - f_st;
// Khoảng cách tới nhân
float dist = length(diff);
// Lưu khoảng cách nhỏ nhất
m_dist = min(m_dist, dist);
...Đoạn code trên lấy cảm hứng từ một bài báo của Inigo's Quilez mà trong đó ông có viết:
"... đoạn code trên có thể cải tiến hơn nữa chỉ nhờ một mẹo nhỏ. Các đoạn code tương tự có rủi ro về sai số, vì vị trí nhân được lưu là toạ độ tuyệt đối. Ta có thể sử dụng các kiểu dữ liệu có độ chính xác cao hơn để khắc phục, nhưng còn cách khác hay hơn. Code của tôi không dùng toạ độ tuyệt đối mà chỉ dùng toạ độ tương đối trong mỗi ô thôi: sau khi tách được phần nguyên và phần thập phân, việc sinh vị trí ngẫu nhiên của nhân được thực hiện giống nhau trong mọi ô, vì thế mà phần nguyên không còn cần thiết nữa, tiết kiệm rất nhiều không gian bộ nhớ. Thực tế thì ở các đoạn code sinh voronoi thông thường, tuy sử dụng toạ độ tuyệt đối nhưng nó vẫn phải đảm bảo nằm trong ô, tức là vẫn có ràng buộc gián tiếp về toạ độ tương đối. Còn ở đoạn code trên, ta thậm chí không cần quan tâm tới ràng buộc đó, bởi toạ độ được sinh ra chắc chắn sẽ nằm trong ô. Mẹo nhỏ này có thể áp dụng cả trong trường hợp số lượng điểm ảnh khổng lồ - ta sẽ cần sử dụng kiểu dữ liệu double có khoảng giá trị lớn hơn float, nhưng ngay sau khi tách được phần thập phân, ta chỉ cần làm việc với phần thập phân lưu bằng một biến float là đủ. Tất nhiên là mẹo này cũng có thể áp dụng cho Perlin noise (nhưng tôi chưa từng thấy nó được implement hay mô tả theo cách này)."
Tóm tắt: Ta chia canvas thành nhiều ô, mỗi ô có một nhân; mỗi điểm ảnh sẽ tính khoảng cách tới nhân trong ô tương ứng và cả 8 ô xung quanh; lưu lại khoảng cách nhỏ nhất. Kết quả thu được là 1 distance field trông như sau:
Hãy thử vài thứ phức tạp hơn:
- Chia canvas thành lưới có kích thước khác
- Làm thế nào để di chuyển các nhân trong mỗi ô ?
- Nếu ta coi vị trí của con trỏ chuột là một nhân thì sao ?
- Nếu không dùng công thức
m_dist = min(m_dist, dist);thì còn cách nào khác để tìm khoảng cách gần nhất không ? - Dùng distance field này tạo được các họa tiết nào ?
Thuật toán này cũng có thể được mô tả theo cách khác, thay vì bắt đầu bằng các điểm ảnh ta sẽ lấy các nhân làm cơ sở. Cụ thể như sau: Mỗi nhân sẽ tự lan rộng vùng ảnh hưởng ra xung quanh tới khi chạm với các vùng ảnh hưởng khác. Trong tự nhiên thì nhiều loài động thực vật trưởng thành theo cách này. Các hình thái sinh vật sống được hình thành bởi hai tác động chính: một là nội lực đẩy từ bên trong ra khiến nó ngày càng sinh sôi và lớn hơn, hai là ngoại lực từ bên ngoài kiềm chế mức độ sinh trưởng lẫn nhau. Thuật toán mô phỏng theo quan sát này được đặt tên theo nhà toán học đã định nghĩa nó, đó là Georgy Voronoi.
Thuật toán Voronoi
Việc tạo ra sơ đồ Voronoi từ cellular noise không khó như hình dung. Ta chỉ cần tốn thêm ít bộ nhớ để lưu các thông tin. Để làm điều đó ta sẽ dùng một biến kiểu vec2 có tên là m_point. Bằng cách lưu lại hướng từ điểm ảnh tới nhân gần nhất, thay vì chỉ có thông tin về khoảng cách, ta còn xác định cả đỉnh gần nhất luôn.
...
if( dist < m_dist ) {
m_dist = dist;
m_point = point;
}
...Trong đoạn code dưới đây, tôi không dùng hàm min nữa mà dùng lệnh if cơ bản. Vì tôi không chỉ muốn lưu lại khoảng cách gần nhất mà còn muốn biết nhân gần nhất nữa (dòng 32 tới 37).
Nếu bạn di chuyển con trỏ chuột trong canvas, bạn sẽ thấy con trỏ chuột cũng được tính là một nhân. Tôi làm vậy để bạn có thể hiểu hơn về thuật toán này. Thậm chí, màu của các pixel sẽ thay đổi theo toạ độ con trỏ chuột.
Giờ hãy chuyển qua thuật toán tương tự được mô tả trong báo cáo của Steven Worley. Bạn hãy tự code thuật toán này. Bạn cũng có thể tham khảo đoạn code dưới đây bằng cách click vào ảnh minh hoạ. Thuật toán ban đầu của Steven Worley có nhiều nhân trong một ô thay vì chỉ có một nhân, nhưng vì ông dùng ngôn ngữ C để lập trình, nên có thể thay đối số vòng lặp tuỳ ý. GLSL không cho phép điều đó, nên ta sẽ giới hạn số nhân ở mỗi ô là 1.
Khi bạn đã hiểu thuật toán này rồi, hãy nghĩ ra cách để tận dụng nó.



Cải tiến Voronoi
Năm 2011, Stefan Gustavson đã cải tiến thuật toán của Steven Worley cho GPU chỉ bằng cách duyệt qua ma trận 2x2 thay vì 3x3. Điều này giúp giảm số lượng phép tính đáng kể, nhưng cũng dễ làm cho các cạnh không đồng đều. Hãy thử nhìn các ví dụ sau:
Khoảng cuối năm 2012, Inigo Quilez đã đăng một bài báo về cách vẽ các đường viền Voronoi một cách chính xác.
Thí nghiệm của Inigo với Voronoi không chỉ dừng lại ở đó. Vào năm 2014, ông đã công bố một nghiên cứu thú vị mà ông gọi là voro-noise, một hàm có khả năng chuyển tiếp giữa nhiễu ngẫu nhiên và Voronoi. Trong báo cáo đó ông có viết:
"Dù cả hai thuật toán sinh nhiễu đều dùng hệ thống lưới nhưng cách dùng rất khác nhau. Value noise thì nội suy giữa các đỉnh có giá trị đi kèm ngẫu nhiên, Gradient noise thì nội suy giữa các dải màu ngẫu nhiên, còn Voronoi thì tính khoảng cách tới các đỉnh ngẫu nhiên. Nếu cả nội suy có lọc bilinear và công thức xác định khoảng cách gần nhất có thể tổng quát hoá thành một phép toán thì cả nhiễu thông thường và sơ đồ Voronoi sẽ được quy về 2 trường hợp của cùng một thuật toán sinh họa tiết trên một lưới xác định phải không ?"
Bạn hãy quan sát thật kỹ thế giới xung quanh, thiên nhiên đầy nhiệm màu và sẽ giúp bạn tự tìm ra kỹ thuật sinh nhiễu của riêng mình !