Cellular Noise (pol. "szum komórkowy")

W 1996 roku, szesnaście lat po oryginalnym algorytmie szumu Perlina i pięć lat przed jego Simplex Noise, Steven Worley napisał pracę zatytułowaną "A Cellular Texture Basis Function". Opisuje w niej technikę teksturowania proceduralnego, która jest obecnie szeroko stosowana przez grafików.

Aby zrozumieć jej zasady, musimy zacząć myśleć w kategoriach iteracji. Zapewne wiesz, co to oznacza: używanie pętli for. Jest tylko jeden haczyk z pętlami for w GLSL: warunek, który sprawdzamy musi być stałą (const). Tak więc nie ma dynamicznych pętli - liczba iteracji musi być stała.

Przyjrzyjmy się przykładowi.

Punkty w polu odległości

Cellular Noise opiera się na polach odległości, a dokładniej odległości do najbliższego ze zbioru punktów. Załóżmy, że chcemy stworzyć pole odległości składające się z 4 punktów. Co musimy zrobić? Cóż, dla każdego piksela chcemy obliczyć odległość do najbliższego punktu. Oznacza to, że musimy iterować po wszystkich punktach, obliczać ich odległości do bieżącego piksela i przechować odległość do tego najbliższego.

    float min_dist = 100.; // Zmienna przechowująca odległość do najbliższego punktu

    min_dist = min(min_dist, distance(st, point_a));
    min_dist = min(min_dist, distance(st, point_b));
    min_dist = min(min_dist, distance(st, point_c));
    min_dist = min(min_dist, distance(st, point_d));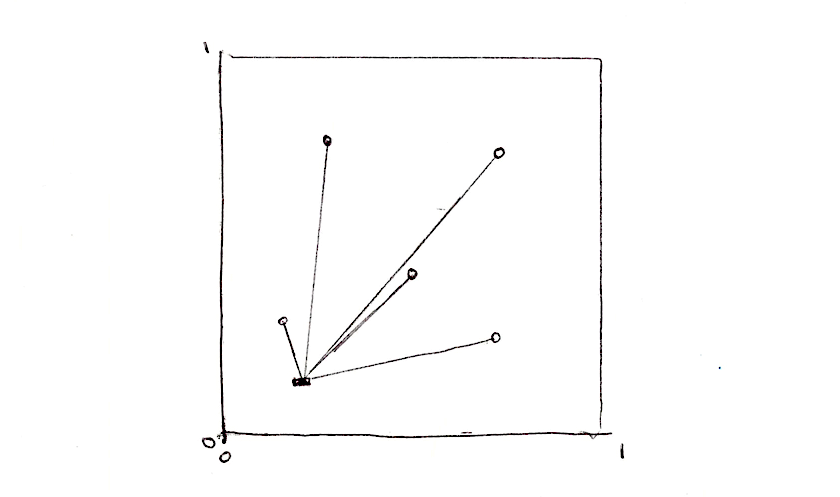

Nie jest to zbyt eleganckie, ale załatwia sprawę. Teraz zaimplementujmy go ponownie, używając tablicy i pętli for.

    float m_dist = 100.;  // minimum distance
    for (int i = 0; i < TOTAL_POINTS; i++) {
        float dist = distance(st, points[i]);
        m_dist = min(m_dist, dist);
    }

Zauważ, jak używamy pętli for do iteracji po tablicy punktów i funkcji min() do śledzenia odległości do najbliższego punktu. Oto krótka działająca implementacja tego pomysłu:

W powyższym kodzie jeden z punktów jest przypisany do pozycji myszy. Pobaw się nim, abyś mógł zrozumieć intuicję stojącą za tym kodem. Następnie spróbuj ćwiczeń:

• Jak można animować pozostałe punkty?
• Po przeczytaniu rozdziału o kształtach, wyobraź sobie ciekawe sposoby wykorzystania tego pola odległości!
• Co, jeśli chcemy dodać więcej punktów do tego pola odległości? Co jeśli chcemy dynamicznie dodawać/odejmować punkty?

Kafelkowanie i iteracja

Zapewne zauważyłeś, że pętle for i tablice nie są zbyt dobrymi przyjaciółmi GLSL. Jak już wspomnieliśmy, pętle nie akceptują dynamicznych warunków wyjścia. Ponadto, iteracja przez wiele instancji znacznie zmniejsza wydajność twojego shadera. Oznacza to, że nie możemy użyć tego prostego, brute-force'owego podejścia dla dużych ilości punktów. Musimy znaleźć inną strategię, taką, która wykorzystuje architekturę przetwarzania równoległego GPU.

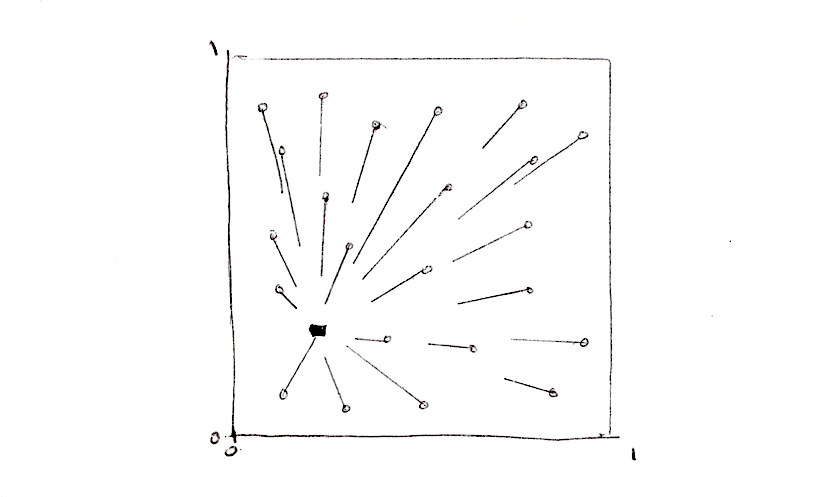
Jednym ze sposobów podejścia do tego problemu jest podzielenie przestrzeni na rozłączne obszary/komórki. Nie każdy piksel musi sprawdzać odległość do każdego punktu, prawda? Biorąc pod uwagę fakt, że każdy piksel działa w swoim własnym wątku, możemy podzielić przestrzeń na komórki, z których każda ma jeden unikalny punkt do oglądania. Ponadto, aby uniknąć aberracji na krawędziach między komórkami musimy sprawdzić odległości do punktów w sąsiednich komórkach. Jest to główna idea artykułu Stevena Worleya. Ostatecznie każdy piksel musi sprawdzić tylko dziewięć pozycji: punkt własnej komórki i punkty w 8 komórkach wokół niego. Dzieliliśmy już przestrzeń na komórki w rozdziałach o: wzorach kafelkowych, losowości i szumie, więc mam nadzieję, że jesteś już zaznajomiony z tą techniką.

    // skalowanie
    st *= 3.;

    // dzielenie przestrzeni na kafelki
    vec2 i_st = floor(st);
    vec2 f_st = fract(st);

Jaki jest więc plan? Użyjemy współrzędnych kafelka (przechowywanych w części całkowitej, i_st) do skonstruowania losowej pozycji punktu. Funkcja random2f, której użyjemy, przyjmuje vec2 i zwraca vec2 z losową pozycją (o wartościach z zakresu od 0.0 do 1.0). Tak więc, dla każdego kafla będziemy mogli otrzymać jeden punkt losowo położony wewnątrz tego kafla.

    vec2 point = random2(i_st);

Każdy piksel wewnątrz tego kafla (przechowywany w części ułamkowej, f_st) sprawdzi swoją odległość do tego nowego, losowego punktu.

    vec2 diff = point - f_st;
    float dist = length(diff);

Wynik będzie wyglądał tak:

Musimy też sprawdzić odległości do punktów w okolicznych kafelkach, a nie tylko do tego w bieżącym kafelku. W tym celu iterujemy po sąsiednich kafelkach. Nie po wszystkich kafelkach, tylko po tych bezpośrednio otaczających bieżącego. Czyli od -1 (lewy) do 1 (prawy) na osi x oraz od -1 (dolny) do 1 (górny) na osi y. Region 3x3 składający się z 9 kafelków może być iterowany przy użyciu podwójnej pętli for, jak poniżej:

for (int y= -1; y <= 1; y++) {
    for (int x= -1; x <= 1; x++) {
        // Względne położenie sąsiadującego kafelka
        vec2 neighbor = vec2(float(x),float(y));
        ...
    }
}

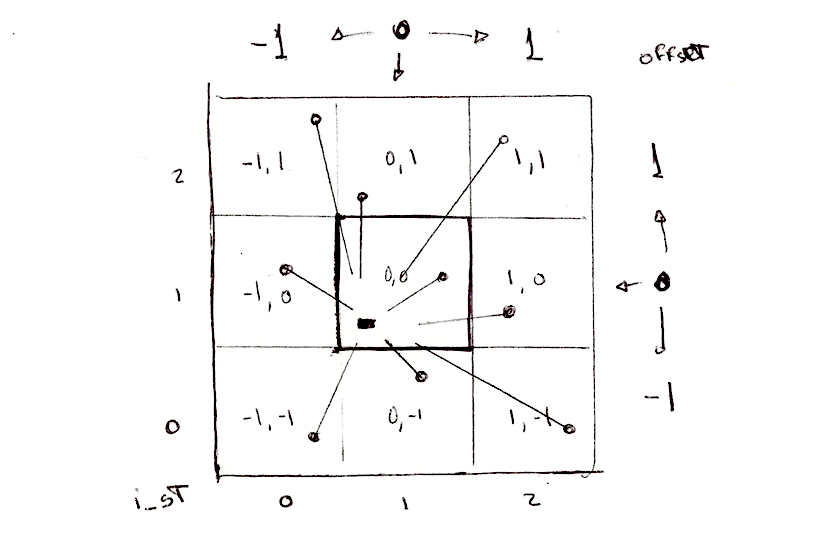
Teraz możemy obliczyć położenie punktów w każdym z sąsiadujących kafelków z pomocą podwójnej pętli for, dodając przesunięcie sąsiedniego kafelka (neighbor) do współrzędnej bieżącego kafelka (i_st).

        ...
        // Losowe położenie punktu wewnątrz sąsiedniego kafelka
        vec2 point = random2(i_st + neighbor);
        ...

Reszta polega na obliczeniu odległości do każdego z sąsiednich punktów i zapisaniu najmniejszej odległości w zmiennej o nazwie m_dist (z ang. "minimal distance").

        ...
        vec2 diff = neighbor + point - f_st;

        // Odległość do punktu
        float dist = length(diff);

        // Zachowaj mniejszą odległość
        m_dist = min(m_dist, dist);
        ...

Powyższy kod jest inspirowany artykułem Inigo Quileza, w którym zauważa, jak problemy z precyzją bitową mogą być uniknięte poprzez przejście do stosowanej już przez nas przestrzeni kafelkowej (w przeciwieństwie do robienia obliczeń w domyślnych współrzędnych, niepodzielonych na części całkowite i ułamkowe):

Podsumowując: dzielimy przestrzeń na kafelki; każdy piksel liczy odległość do punktu w swoim własnym kafelku i odległość do punktów z otaczających go 8 kafelków; przechowuje najbliższą odległość. Wynikiem jest pole odległości, które wygląda jak w poniższym przykładzie:

Eksploruj tę ideę dalej:

• Przeskaluj przestrzeń o różne wartości.
• Czy możesz wymyślić inne sposoby animacji punktów?
• Co jeśli chcemy obliczyć dodatkowy punkt z pozycji myszy?
• Jakie inne sposoby konstruowania tego pola odległości możesz sobie wyobrazić, poza m_dist = min(m_dist, dist);?
• Jakie ciekawe wzory można stworzyć za pomocą tego pola odległości?

Algorytm ten można również interpretować z perspektywy punktów, a nie bieżących pikseli. W takim przypadku można go opisać jako: każdy punkt rośnie, dopóki nie znajdzie rosnącego obszaru innego punktu. Odzwierciedla to niektóre z zasad wzrostu w naturze. Żywe formy kształtowane są przez napięcie między wewnętrzną siłą do rozszerzania się i wzrostu oraz zewnętrznymi siłami ograniczającymi. Klasyczny algorytm symulujący to zachowanie nazwany został za Georgy Voronoi.

Algorytm Voronoi

Konstruowanie diagramów Voronoi z szumu komórkowego jest mniej trudne niż mogłoby się wydawać. Musimy tylko zachować pewną dodatkową informację o punkcie, który jest najbliżej bieżącego piksela. Do tego celu użyjemy vec2 o nazwie m_point (z ang. "minimal point"). Przechowując wektor od bieżącego piksela do najbliższego punktu (zamiast samej odległości) będziemy "przechowywać" "unikalny" identyfikator tego punktu.

    ...
    if( dist < m_dist ) {
        m_dist = dist;
        m_point = point;
    }
    ...

Zauważ, że w poniższym kodzie nie używamy już min do obliczania najbliższej odległości, ale zwykłegpo warunku if. Dlaczego? Ponieważ chcemy zrobić coś więcej za każdym razem, gdy pojawi się nowy bliższy punkt, a mianowicie zapisać jego pozycję (linie 32 do 37).

Zauważ, jak kolor ruchomej komórki (związanej z pozycją myszy) zmienia kolor w zależności od jej położenia. To dlatego, że kolor jest przypisywany przy użyciu wartości (pozycji) najbliższego punktu.

Podnieśmy poprzeczkę, przechodząc na podejście z artykułu Stevena Worleya. Spróbuj zaimplementować to samodzielnie. Możesz skorzystać z pomocy poniższego przykładu, klikając na niego. Zauważ, że oryginalne podejście Stevena Worleya używa zmiennej liczby punktów dla każdego kafla, więcej niż jeden w większości kafli. W tej jego nie-shaderowej implementacji (bo w C, a nie w GLSL) pomaga to przyspieszyć pętlę poprzez wczesne jej opuszczanie. Pętle GLSL nie pozwalają na zmienną liczbę iteracji, więc prawdopodobnie chcesz trzymać się jednego punktu na kafelek.

Gdy już rozgryziesz ten algorytm, pomyśl o ciekawych i kreatywnych jego zastosowaniach.

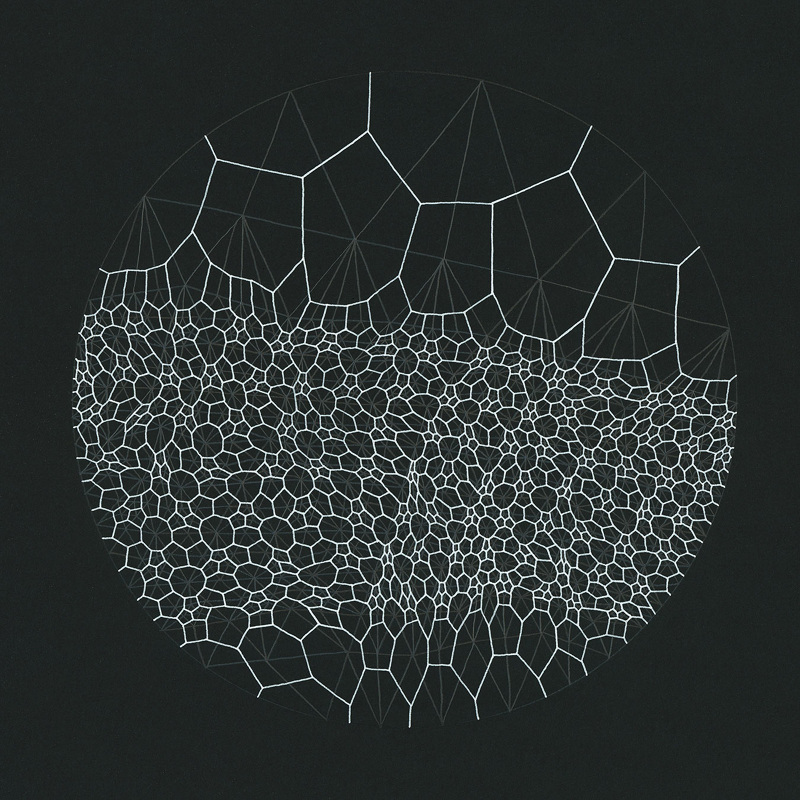
Ulepszenie Voronoi

W 2011 roku Stefan Gustavson zoptymalizował algorytm Stevena Worleya pod GPU, iterując tylko przez macierz 2x2 zamiast 3x3. To znacznie zmniejsza ilość pracy, ale może tworzyć artefakty w postaci nieciągłości na krawędziach między kafelkami. Przyjrzyj się poniższym przykładom.

Później w 2012 roku Inigo Quilez napisał artykuł o tym, jak zrobić Voronoi z ostrymi granicami.

Eksperymenty Inigo z Voronoi nie skończyły się na tym. W 2014 roku napisał artykuł o tym, co nazywa voro-noise. Jest to funkcja, która pozwala na stopniowe interpolowanie między zwykłym szumem a Voronoi. Jego słowami:

"Pomimo tego podobieństwa, faktem jest, że sposób użycia kafelkowania w obu metodach jest inny. Szum interpoluje/uśrednia wartości losowe (jak w Value Noise) lub gradienty (jak w Gradient Noise), podczas gdy Voronoi oblicza odległość do najbliższego punktu w kafelku. Interpolacja dwuliniowa (ang. "bilinear") i wartość minimalna to dwie bardzo różne operacje, ale czy na pewno? Czy można je połączyć w bardziej ogólną metrykę? Gdyby tak było, to zarówno szum jak i Voronoi mogłyby być postrzegane jako szczególne przypadki bardziej ogólnego generatora wzorów kafelkowych?".

Teraz nadszedł czas, abyś przyjrzał się bliżej rzeczom, zainspirował się naturą i znalazł swoje własne ujęcie tej techniki!