算法绘画
造型函数
这一章应该叫做宫城先生的粉刷课(来自电影龙威小子的经典桥段)。之前我们把规范化后的 x,y 坐标映射(map)到了红色和绿色通道。本质上说我们是建造了这样一个函数:输入一个二维向量(x,y),然后返回一个四维向量(r,g,b,a)。但在我们跨维度转换数据之前,我们先从更加…更加简单的开始。我们来建一个只有一维变量的函数。你花越多的时间和精力在这上面,你的 shader 功夫就越厉害。

接下来的代码结构就是我们的基本功。在它之中我们对规范化的 x 坐标(st.x)进行可视化。有两种途径:一种是用亮度(度量从黑色到白色的渐变过程),另一种是在顶层绘制一条绿色的线(在这种情况下 x 被直接赋值给 y)。不用过分在意绘制函数,我们马上会更加详细地解释它。
简注 :vec3 类型构造器“明白”你想要把一个值赋值到颜色的三个通道里,就像 vec4 明白你想要构建一个四维向量,三维向量加上第四个值(比如颜色的三个值加上透明度)。请参照上面示例的第 19 到 25 行。
这些代码就是你的基本功;遵守和理解它非常重要。你将会一遍又一遍地回到 0.0 到 1.0 这个区间。你将会掌握融合与构建这些代码的艺术。
这些 x 与 y(或亮度)之间一对一的关系称作线性插值(linear interpolation)。(译者注:插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。因为对计算机来说,屏幕像素是离散的而不是连续的,计算机图形学常用插值来填充图像像素之间的空隙。)现在起我们可以用一些数学函数来改造这些代码行。比如说我们可以做一个求 x 的 5 次幂的曲线。
很有趣,对吧?试试看把第 19 行的指数改为不同的值,比如:20.0,2.0,1.0,0.0,0.2 或 0.02。理解值和指数之间的关系非常重要。这些数学函数可以让你灵动地控制你的代码,就像是给数据做针灸一样。
pow() (求x的y次幂)是 GLSL 的一个原生函数,GLSL 有很多原生函数。大多数原生函数都是硬件加速的,也就是说如果你正确使用这些函数,你的代码就会跑得更快。
换掉第 19 行的幂函数,试试看exp()(以自然常数e为底的指数函数),log()(对数函数) 和 sqrt()(平方根函数)。当你用 Pi 来玩的时候有些方程会变得更有趣。在第 5 行我定义了一个宏,使得每当程序调用 PI 的时候就用 3.14159265359 来替换它。
Step 和 Smoothstep
GLSL 还有一些独特的原生插值函数可以被硬件加速。
step() 插值函数需要输入两个参数。第一个是极限或阈值,第二个是我们想要检测或通过的值。对任何小于阈值的值,返回 0.0,大于阈值,则返回 1.0。
试试看改变下述代码中第 20 行的值。
另一个 GLSL 的特殊函数是 smoothstep()。当给定一个范围的上下限和一个数值,这个函数会在已有的范围内给出插值。前两个参数规定转换的开始和结束点,第三个是给出一个值用来插值。
在之前的例子中,注意第 12 行,我们用到 smoothstep 在 plot() 函数中画了一条绿色的线。这个函数会对给出的 x 轴上的每个值,在特定的 y 值处制造一个凹凸形变。如何做到呢?通过把两个 smoothstep() 连接到一起。来看看下面这个函数,用它替换上面的第 20 行,把它想成是一个垂直切割。背景看起来很像一条线,不是吗?
float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);正弦和余弦函数
当你想用数学来制造动效,形态或去混合数值,sin 和 cos 就是你的最佳伙伴。
这两个基础的三角函数是构造圆的极佳工具,就像张小泉的剪刀一样称手。很重要的一点是你需要知道它们是如何运转的,还有如何把它们结合起来。简单来说,当我们给出一个角度(这里采用弧度制),它就会返回半径为一的圆上一个点的 x 坐标(cos)和 y 坐标(sin)。正因为 sin 和 cos 返回的是规范化的值(即值域在 -1 和 1 之间),且如此流畅,这就使得它成为一个极其强大的工具。
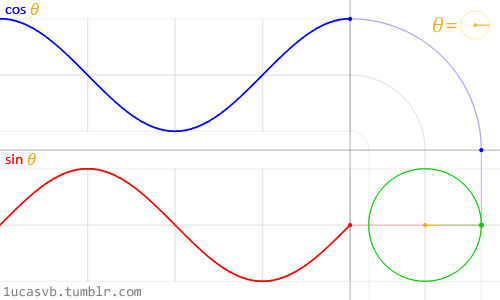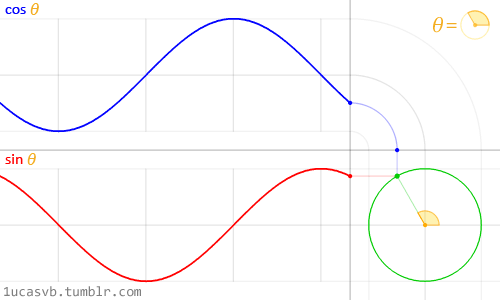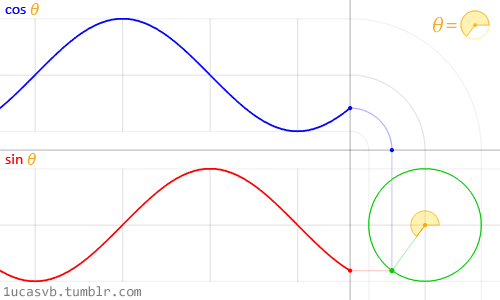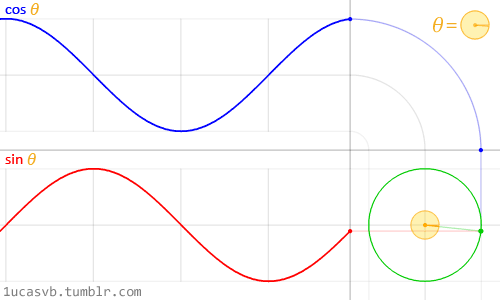
尽管描述三角函数和圆的关系是一件蛮困难的事情,上图动画很棒地做到了这一点,视觉化展现了它们之间的关系。
仔细看 sin 曲线。观察 y 值是如何平滑地在 +1 和 -1 之间变化。就像之前章节关于的 time 的例子中,你可以用 sin() 的有节奏的变动给其他东西加动效。如果你是在用浏览器阅读的话你可以改动上述公式,看看曲线会如何变动。(注:不要忘记每行最后要加分号!)
试试下面的小练习,看看会发生什么:
-
在
sin里让 x 加上时间(u_time)。让sin 曲线随 x 轴动起来。 -
在
sin里用PI乘以 x。注意 sin 曲线上下波动的两部分如何收缩了,现在 sin 曲线每两个整数循环一次。 -
在
sin里用时间(u_time)乘以 x。观察各阶段的循环如何变得越来越频繁。注意 u_time 可能已经变得非常大,使得图像难以辨认。 -
给
sin(x)(注意不是 sin 里的 x)加 1.0。观察曲线是如何向上移动的,现在值域变成了 0.0 到 2.0。 -
给
sin(x)乘以 2.0。观察曲线大小如何增大两倍。 -
计算
sin(x)的绝对值(abs())。现在它看起来就像一个弹力球的轨迹。 -
只选取
sin(x)的小数部分(fract())。 - 使用向正无穷取整(
ceil())和向负无穷取整(floor()),使得 sin 曲线变成只有 1 和 -1 的电子波。
其他有用的函数
最后一个练习中我们介绍了一些新函数。现在我们来一个一个试一遍。依次取消注释下列各行,理解这些函数,观察它们是如何运作的。你一定在奇怪……为什么要这么做呢?Google 一下“generative art”(生成艺术)你就知道了。要知道这些函数就是我们的栅栏。我们现在控制的是它在一维中的移动,上上下下。很快,我们就可以尝试二维、三维甚至四维了!

造型函数进阶
Golan Levin 写过关于更加复杂的造型函数的文档,非常有帮助。把它们引入 GLSL 是非常明智的选择,这将是你的代码的广阔的素材库
-
多项式造型函数(Polynomial Shaping Functions): www.flong.com/archive/texts/code/shapers_poly
-
指数造型函数(Exponential Shaping Functions): www.flong.com/archive/texts/code/shapers_exp
-
圆与椭圆的造型函数(Circular & Elliptical Shaping Functions): www.flong.com/archive/texts/code/shapers_circ
- 贝塞尔和其他参数化造型函数(Bezier and Other Parametric Shaping Functions): www.flong.com/archive/texts/code/shapers_bez
就像厨师自主选择辣椒和各种原料,数字艺术家和创意编程者往往钟情于使用他们自己的造型函数。
Iñigo Quiles 收集了一套有用的函数。在看过这篇文章后,看看下列函数转换到 GLSL 的样子。注意那些细小的改变,比如给浮点数(float)加小数点“.”,给“C 系函数”换成它们在 GLSL 里的名字,比如不是用 powf() 而是用 pow():
给你们看些东西刺激一下斗志,这里有一个非常优雅的例子(作者是 Danguafer,造型函数的空手道黑带)。
在下一章我们会有一些新的进展。我们会先混合各种颜色,然后画些形状。
练习
来看看 Kynd 帮大家制作的公式表。看他如何结合各种函数及它们的属性,始终控制值的范围在 0.0 到 1.0。好了,现在是你自己练习的时候了!来试试这些函数,记住:熟能生巧。

填充你的工具箱
这里有一些工具可以帮你更轻松地可视化这些函数。
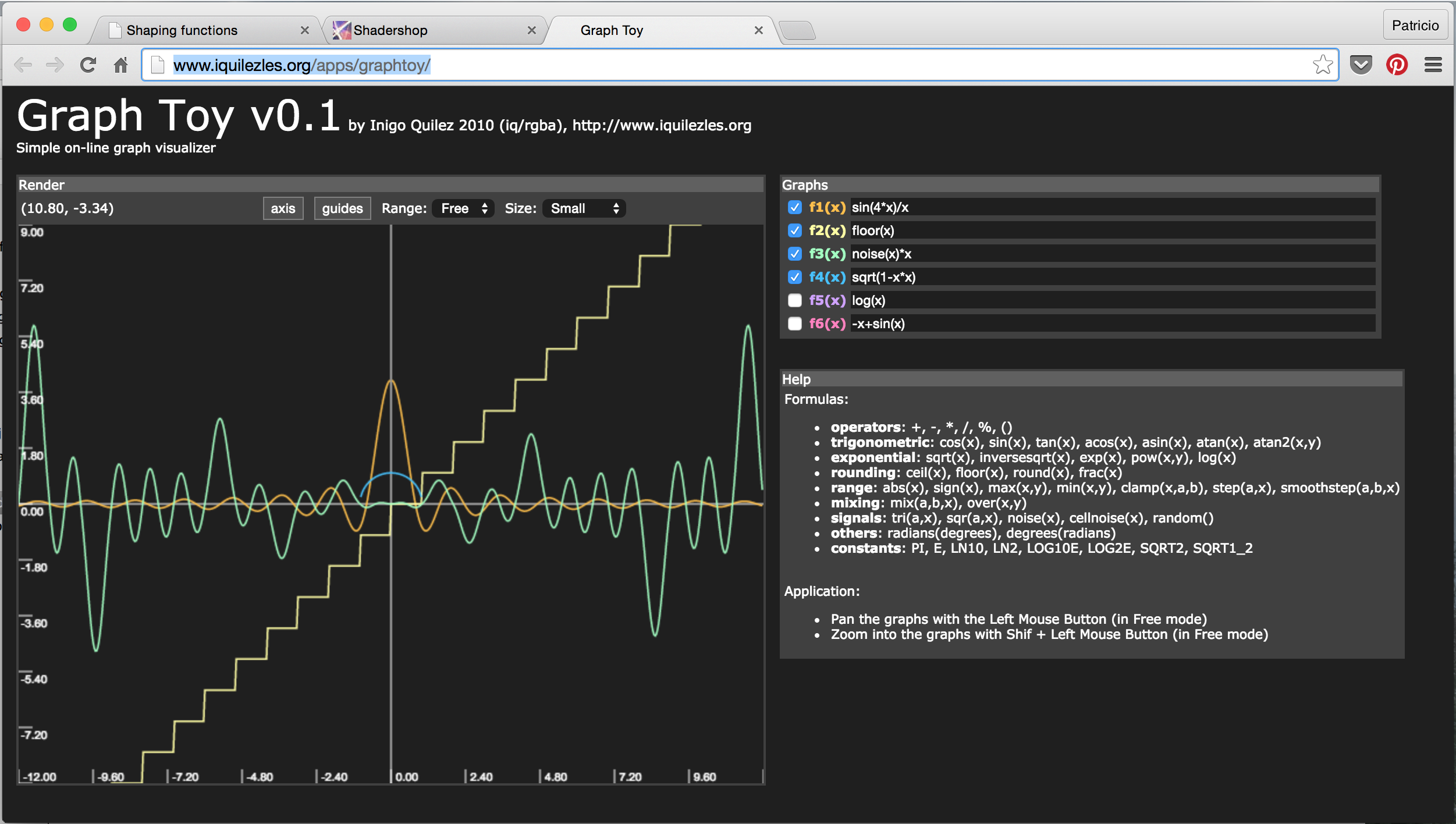
- GraphToy:仍然是 Iñigo Quilez 为大家做的工具,用于在 WebGL 中可视化 GLSL 函数。
- LYGIA Shader Library a shader library of reusable functions that can be include easily on your projects. It's very granular, designed for reusability, performance and flexibility. And can be easily be added to any projects and frameworks.