Algorithmic drawing

Shaping functions

이번 챕터는 "미야기씨의 울타리 수업"이라고 표현할수 있겠다. 전에는, 노멀라이즈된 ,x와 y를 red와 green채널들에 적용해 보았다. 원래는 2차원 벡터(x and y)를 받아, 4차원 벡터(r, g, b and a)를 리턴하는 함수가 좀더 자연스럽니다. 하지만 지금 이런문제를 해결하기 전에, 간단한것부터 시작해보자... 훨씬더 간단한것부터. 이말은 1차원 함수에 대한 정의에서부터 시작한다. 시간과 에너지를 많이 투자하고 배우고 마스터하려고 하다보면, 우리는 더욱더 강한 쉐이더 카라테를 배울수 있을것이다.

베스트 키드 (1985)

아래 코드는 우리의 울타리가 될것이다. 여기서 우린 x 위치정보(st.x)의 노멀라이즈된 값을 2가지 방법으로 시각화 하는데: 하나는 밝기로 (검은색에서 흰색으로 잘 묻어져 나가는 색), 다른 하나는 그 위에 초록색 선( x 값이 바로 y 값에 적용된)으로 나타낼 것이다. 지금은 선을 그리는 함수에 대해 너무 신경쓰지말자. 그부분은 나중에 더 자세히 다루게 될것이다.

퀵노트: vec3 타입 생성자는 유저가 세가지 컬러 채널들을 입력하려는 것을 "이해" 한다. 또한, vec4 타입생성자역시, 3차원 벡터와, 1개의 실수(보통 alpha나 opacity라고 일컫는)로 이루어진 4차원 벡터를 만들려고 한다는 점 또한 이해한다. 라인 19과 25을 위에 코드에서 찾아보라.

이 코드는 다시한번 당신의 울타리이다; 받아들이고 이해하는것이 중요하다. 앞으로도 계쏙 이 0.0 에서 1.0의 공간을 계속 사용하게 될것이다. 여기서 당신은 블렌딩과, 선그리기를 마스터 해야한다.

x와 y (또는 밝기)의 1:1 대응은 흔히 선형 보간법 이라고 알려져 있다. 여기서 우린 수학적 함수로 선을 그릴수 있다. 예로, x값이 지수로 5를 갖는다면 이 선은 구부러 진다.

흥미로운일이지 않은가? 라인 19에서 다른 값들을 시도해보자: 20.0, 2.0, 1.0, 0.0, 0.2, 0.02. 지수를 통해 나오는 값에 대한 상관관계를 이해하는 것은 앞으로 매우 유용한 권법이 될것이다. 이런 종류의 수학적 함수를 코드의 공간에서 이용하는것은 엄청난 표현 컨트롤을 할수 있도록 허용한다. 마치 데이터를 이용한 한방권법이라고 저자는 소개한다.

pow() 는 GLSL의 내장형 함수이고 GLSL은 이런 수학함수를 많이 제공한다. 거의 모든 함수들은 하드웨어 레벨에서 구동되도록 '가속화' 되어 있다. 다시말해, 이런 이점을 잘 활용하면 굉장히 빠른 코드를 쓸수 있게 된다.

라인 19의 power 함수를 다른 함수로 교체해보자.: exp(), log(), sqrt(). 어떤함수들은 인자로 PI값을 넣었을때 재밌는 결과를 내기도 한다. 라인 5에 PI값을 3.14159265359로 define해 둔것을 알수 있다.

Step and Smoothstep

GLSL에는 하드웨어 가속화된 내장 보간법 함수들이 존재한다.

step() 보간법은 2개의 인자를 받는다. 첫번째것은 경계나, 한계점이고, 두번째것은 체크하거나 넘길 값이다. 어떤값이든 이 한계점보다 낮은 값은 0으로 처리되어 리턴될것이고, 한계점보다 높은 값은 1.0으로 처리되어 리턴될것이다.

라인 20의 한계점 값을 바꾸어 보자.

또 하나의 잘 알려진 함수중 하나는 smoothstep()이다. 두값의 레인지를 주고, 그 사이의 값으로 보간시켜주는 방법이다. 처음 두개의 인자는 레인지의 시작점과 끝점이고, 세번째 인자는 두 점사이에서 보간되고 리턴되는 값이다.

전 예제의 라인 12를 보면, smoothstep을 plot()에 사용하여 초록색 선을 그린것을 알수 있다. 각 x값에 대한 y값을 bump시킨 것으로 표현되고 있는데. 실제로 smoothstep() 를 통해 그려진 쉐이프 A를 같은 방법으로 그려진 쉐이프 B에서 그냥 빼준것이다. 아래 예제를 보고 라인 20과 바꿔보아라. ght?

    float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);

Sine과 Cosine 함수

수학으로 애니메이션, 쉐이프등을 만들거나 섞을때는, sine과 cosine만큼 좋은 친구도 없다.

이 두개의 삼각함수로 원을 그리는 유명한 예제를 보면 마치 맥가이버의 스위스 군용 나이프와도 같다. 이들이 왜 이렇게 작동되고, 서로 영향을 주는지 확실히 이해를 해볼 필요가 있다. 요약하자면, 이 함수들로 전해지는 인자값(흔히 radians 값)에 따라, 반지름이 1인 동그라미 모양을 그리는 선 위에 모든 x (cosine) 와 y (sine)가 나타내어 진다고 볼수 있다. 그리고, 이 값들은 노멀라이즈된 값(-1 에서 1 사이의 값)으로 리턴되는 이 방식은 굉장히 유용한 툴로 알려져 있다.

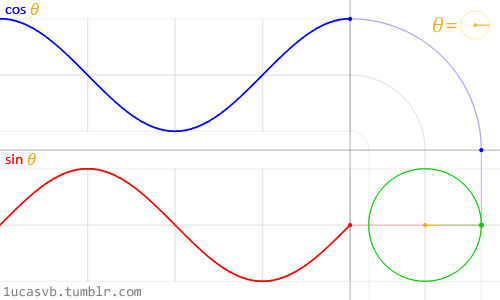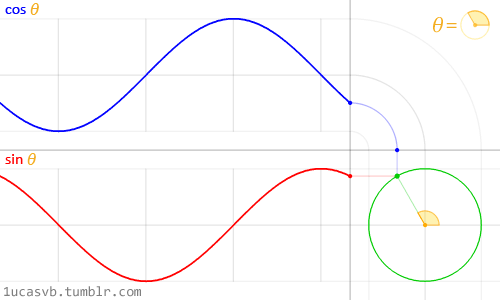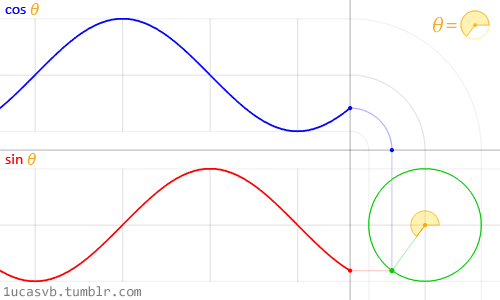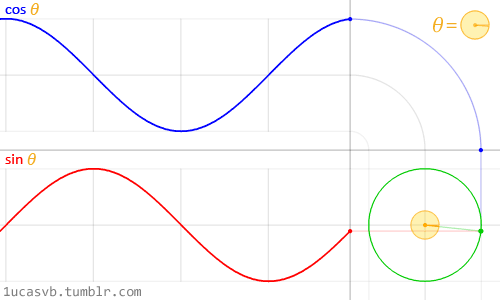
삼각함수들과 동그라미에 대한 해석등을 전부 다를수는 없지만, 위에 애니메이션을 통해 이들이 할수 있는 일이 얼마나 간단하고 아름다운지 살펴볼수 있다.

전 챕터의 time 예제에서 봤듯이, sine wave를 통해, y값이 얼마나 부드럽게 +1에서 -1으로 이동되는지 확인해보라. sin()의 리드믹한 결과값은 애니메이션에 굉장히 유용하다. 브라우져에서 이 예제를 읽고 있다면 코드를 변경해서 변화를 시도해보자. (노트: 끝에 semicolon은 까먹지 말고 붙히자.)

아래의 예제들을 실행해보고, 어떤일들이 벌어지는지 관찰해보자:

sin을 계산하기 전에 time(u_time)을 x 적용해보자. x에 대한 움직임을 습득해보자.
sin을 계산하기 전에 x에 PI를 곱해보자. 반복구간이 좁혀 지는것을 확인할수 있다.
time (u_time) 와 x값을 sin에 적용되기 전에 곱해보자. *반복성이 잦아지는것을 확인할수 있다. u_time이 커지면서 그래프를 점차 읽기 힘들어지게 된다는 것 또한 확인할수 있다.
sin(x)에 1.0을 더해보자. 전체 웨이브가 이동 되는 것을 확인할수 있다. 이제 모든 값들은 0.0에서 2.0사이로 구간이 바뀌었다.
sin(x)에 2.0을 곱해보자. 웨이브의 전체적 강도가 2배로 변하는 것을 알수 있다.
절대값(abs())을 sin(x)에 적용해보자. 공이 튕기는것 같은 효과를 볼수 있다.
소수점 구간(fract())만 취하고, 이를 sin(x)에 적용해보자.
올림 (ceil())된 수나 내림(floor())된 수 역시 sin(x)에 적용해보고, -1에서 1값이 어떻게 리턴되는지 살펴보자.

키타 유용한 함수들

마지막에 여러 새로운 함수들을 소개했다. 이제 이들을 가지고 하나씩 적용을 해볼차례이다. 하나씩 uncomment를 하면 결과를 확인할수 있을것이다.이들에 대해 샅샅히 파내어 익혀보자. 혹시나 왜그래야 하는지에 대한 의문이 든다면, 좋은 대답중 하나는 "generative art"에 대한 것이다. 이 함수들이 우리의 울타리 하는 것을 생각하자. 우리는 지금 1차원에서 권법을 연마하는 중인것이다. 곧, 2차원, 3차원, 4차원까지 우리는 진입하게 될것이다!

Anthony Mattox (2009)

고급 쉐이핑 함수들

Golan Levin 는 제법 복잡하지만 굉장히 유용한 쉐이핑 함수들을 잘 정리해 두었다. 이들을 GLSL로 포팅하는것또한 굉장히 유용한 공부방법일 것이다. 자신만의 쉐이핑 펑션 라이브러리를 개설해보자.

요리사가 자신만의 요리재료와 소스 노하우를 모으듯, digital artist들이나, creative coder들 역시 그들만의 쉐이핑 펑션을 만드는 버릇을 가져야 할것이다.

[Iñigo Quiles](http://www .iquilezles.org/)가 가지고 있는 useful functions정리는 매우 유용하다. 이 글을 읽고, GLSL로 번역해보는 작업도 해볼수 있다. 조심해야 될 점들은, "."(점)을 실수 뒤에 꼭 넣어야 한다는 점이다. 함수의 이름이 powf() 에서 pow()등으로 바뀌어 구현되는 점등이다.

계속 작업이 뜨겁게 진행되는것을 도울수 있게 여기 멋진 작업도 소개해본다. (made by Danguafer)

다음 >> 챕터에서 우리는 새로운 동작에 대해 배우게 될것이다. 색에 조합에 대해 배우고, 쉐이프를 창조하는 작업일것이다.

연습

아래의 공식 테이블을 한번 살펴보자. Kynd 수학함수들이 서로 어떻게 섞여지는지 살펴보고, 이 값들이 0.0에서 1.0사이에서 어떻게 바뀌어 가는지 보자. 이제 스스로 함수들을 복제하고 조합해볼 차례이다. 기억하자. 연습을 할수록 당신의 카라테가 늘게 될것이라는 것을.

Kynd - www.flickr.com/photos/kynd/9546075099/ (2013)

당신의 툴박스를 위해

수학함수를 쉽게 시각화 할수있는 툴을 소개해보고자 한다.

GraphToy: Iñigo Quilez의 GLSL함수들을 WebGL에서 시각화 하는 툴이다.

Iñigo Quilez - GraphToy (2010)

LYGIA Shader Library a shader library of reusable functions that can be include easily on your projects. It's very granular, designed for reusability, performance and flexibility. And can be easily be added to any projects and frameworks.