The Book of Shaders by Patricio Gonzalez Vivo & Jen Lowe

Bahasa Indonesia - Tiếng Việt - 日本語 - 中文版 - 한국어 - Español - Portugues - Français - Italiano - Deutsch - Русский - Polski - English

Dessin Algorithmique

Fonctions de formes

Ce chapitre aurait pu s'appeler "la palissade de monsieur Miyagi" (pour ceux qui n'étaient pas nés en 1984).

Au chapitre précédent, nous avons mappé les coordonnées x et y normalisées sur les canaux rouge et vert. Nous avons créé une fonction qui prend un vecteur à deux dimensions (x et y) et retourne un vecteur à quatre dimensions (r, g, b et a). Avant de transformer des données à plusieurs dimensions, il nous faut commencer par des choses simples... beaucoup plus simples. Concrètement, nous devons comprendre commment marchent les fonctions à une dimension. Plus vous passerez de temps à apprendre et à maîtriser ces fonctions, plus votre Karaté-Shader sera redoutable.

The Karate Kid (1984)

Le code suivant sera notre palissade. Sur cette palissade, nous visualisons la valeur normalisée de la position x (st.x) de deux façons : la luminosité (c'est le joli dégradé du noir au blanc en arrière plan) et une ligne verte dessinée par dessus (dans ce cas, la valeur x est assignée directement à y). Ne vous focalisez pas trop sur la fonction plot pour l'instant, nous y reviendrons en détail dans un moment.

Note: Le constructeur du type vec3, un vecteur à 3 dimensions (r,g,b ou x,y,z ; c'est la même chose), "comprend" que vous allez le construire avec la même valeur pour les trois canaux / dimensions. Il est donc possible d'ecrire vec3 color = vec3(y); pour construire un vecteur à 3 dimensions. Ce vecteur aura la valeur y assignée à chaque canal / dimension soit : color.x = color.y = color.z = y ou color.r = color.g = color.b = y (puisqu'on peut accéder aux variables du vecteur des 2 manières). Le constructeur du type vec4 en revanche, "comprend" que vous allez le construire, soit en passant quatre valeurs dinstinctes : vec4(0., 0.5, 1., 1.), soit en lui passant un vec3 et un float (un nombre) : vec4(color, 1.). Dans notre cas, la valeur du second paramètre (le float), permet de gérer l'opacité aussi appelé l'alpha. Référez vous aux lignes 19 et 25 dans l'exemple ci-dessus pour bien voir la différence de construction des 2 types.

Ce code sera votre palissade ; il est important de bien l'observer et de bien le comprendre. Vous reviendrez souvent dans cet espace entre 0.0 et 1.0 pour maîtriser l'art de le transformer et de sculpter cette ligne.

La relation entre x et y (la luminosité du dégradé), s'appelle une interpolation. Comme on passe une seule valeur (y) à la variable color, on obtient un niveau de gris et comme la valeur de x est normalisée, elle est comprise entre 0.0 et 1.0, on obtient un dégradé du noir (x=0.) au blanc (x=1.). L'interpolation est un principe fondamental ; elle nous permet de faire passer progressivement une valeur de A vers B en fonction d'une troisième valeur T normalisée entre 0.0 et 1.0. La ligne verte reflète ce qui se passe lors de l'interpolation, en l'occurrence, c'est une ligne droite puisque x passe de 0.0 à 1.0 de façon linéaire (x va de 0.0 à 1.0 de façon continue). A partir de là, nous pouvons utiliser des fonctions mathématiques pour sculpter la ligne. Par exemple, on peut passer x à la puissance 5 pour créer une ligne courbe.

Intéressant n'est-ce-pas ? A la ligne 19, au lieu de 5.0 essayez différents exposants, par exemple: 20.0, 2.0, 1.0, 0.0, 0.2 et 0.02. Comprendre la relation qui existe entre la valeur et l'exposant va nous être très utile. Ce genre de fonction mathématique nous donne un contrôle sur l'expressivité du code, c'est une sorte d'acupuncture qui permet de contrôle les flux de valeurs.

pow() est une fonction native de GLSL et il y en a de nombreuses autres. La plupart sont accélérées matériellement, ce qui signifie que si on les utilise bien et avec parcimonie, elle permettent au code de s'exécuter plus vite.

Essayez de remplacer la fonction pow() ligne 19 par: exp(), log() ou sqrt(). Certaines de ces fonctions deviennent vraiment intéressantes quand on les utilise avec PI. Vous pouvez voir que j'ai déclaré une macro qui remplacera chaque appel à PI par la valeur 3.14159265359. Par exemple : sin(st.x * PI), produira une parabole, pow(sin(st.x * PI), 5.) effectuera un pincement de la parabole.

Step et Smoothstep

GLSL propose également des fonctions d'interpolation natives et accélérées matériellement.

La fonction step() prend 2 paramètres, le premier est une limite ou un seuil et le second est la valeur à tester. Toute valeur inférieure au seuil renverra 0.0 tandis que toute valeur supérieure au seuil renverra 1.0.

Essayez de changer la valeur de seuil à la ligne 20 du code suivant :

L'autre fonction d'interpolation s'appelle smoothstep(). Avec deux nombres A et B et une valeur d'interpolation T comprise entre 0.0 et 1.0, elle nous permet de passer de progressivement (et en souplesse) de A à B en fonction de T. Les deux premiers arguments sont les bornes (A et B) et le troisième est la valeur d'interpolation (T).

Dans l'exemple ci-dessus, ligne 12, vous remarquez qu'on a utilisé smoothstep() depuis le début dans la fonction plot() qui permet de dessiner la ligne verte. Pour chaque position le long de l'axe des x, cette fonction crée une bosse à un endroit précis de l'axe des y. Comment ? en combinant deux appels à smoothstep(). Remplacez la ligne 20 par la fonction suivante et regardez l'arrière plan, on dirait une ligne floutée non ? En rapprochant les valeurs de seuil des smoothstep() (0.45, 0.5 et 0.5, 0.55 par exemple), la ligne devient plus fine et moins floue.

float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);

Sinus et Cosinus

Le mieux, si vous voulez utiliser les maths pour animer ou passer d'une valeur à une autre, c'est d'être copain avec les sinus et cosinus.

Ces deux fonctions trigonométriques combinées permettent de dessiner des cercles qui sont plus utiles que le couteau suisse de MacGyver. Il est important de comprendre ce qu'elles font et comment les combiner. Dans un mouchoir de poche, à partir d'un angle en radians (1 radian = PI / 180), le cosinus renvoie la position x et le sinus renvoie la position y d'un point sur un cercle de rayon 1. Le fait que ces fonctions renvoient des valeurs normalisées (entre -1 et 1) de manière très "continue" ou très "souple", en fait un outil indispensable.

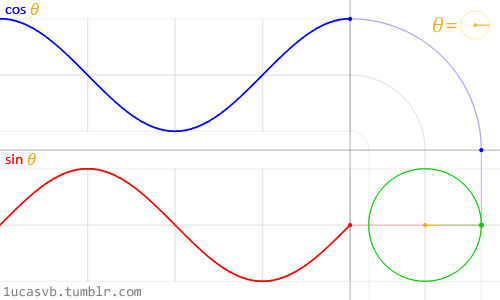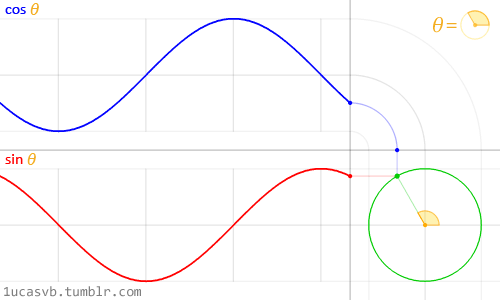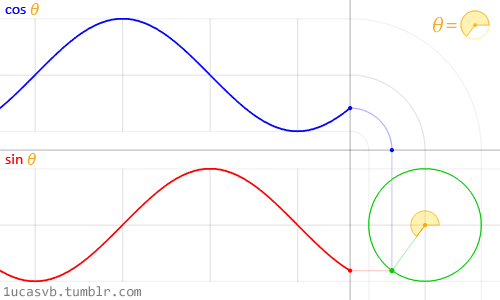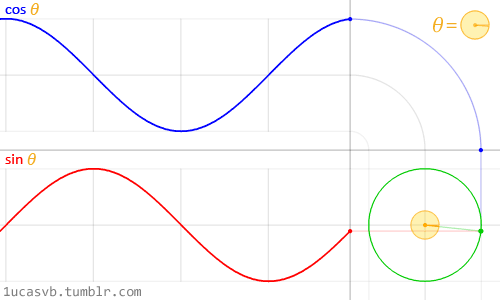
S'il est difficile de comprendre cette relation entre sinus / cosinus et le cercle unitaire (de rayon 1), l'animation ci-dessus la résume assez bien visuellement.

Regardez attentivement cette sinusoïde et surtout comment la valeur y oscille entre -1 et 1. Comme nous l'avons vu sur l'exemple du temps au chapitre 3, on peut utiliser cette propriété temporelle de sin() pour animer une valeur. Si vous regardez cet exemple dans un navigateur, vous pouvez changer le code de la formule ci-dessus pour voir comment la sinusoïde change (n'oubliez pas le point-virule en fin de ligne).

Essayez les changements suivants et regardez ce qui se passe :

Quelques fonctions indispensables

A la fin de l'exercice précédent, nous avons présenté quelques nouvelles fonctions, nous allons maintenant les tester. Pour ce faire, décommentez une ligne à la fois dans la liste suivante. Essayez de comprendre comment chacune fonctionne et comment vous pourriez les combiner. Vous vous demandez sans doute mais... pourquoi ? Une petite recherche de "generative art" sur Google vous apportera la réponse. Gardez à l'esprit que ces fonctions sont votre palissade, nous apprenons à maîtriser le mouvement sur une dimension, de bas en haut, puis de haut en bas. Bientôt, nous utiliserons, deux, trois et même quatre dimensions!

Anthony Mattox (2009)

Fonctions de formes avancées

Golan Levin a écrit quelques articles très instructifs sur des fonctions plus complexes. Les porter en GLSL est une bonne idée si vous souhaitez construire votre boîte à outils.

Comme un chef qui collectionnerait les épices et autres ingrédients exotiques, les artistes digitaux et les codeurs créatifs en particulier aiment travailler leurs propres fonctions de forme.

Iñigo Quiles a écrit une liste de fonctions utiles. Après avoir lu cet article regardez leur traduction en GLSL. Notez bien les petits changements nécessaires, comme le "." (point) sur les floats et l'utilisation des conventions de nommage GLSL pour les fonctions C ; par exemple powf() devient pow():

Pour vous motiver, voici un exemple élégant, fait par Danguafer qui montre le karaté des fonctions de formes.

Au prochain chapitre, nous utiliserons ces nouveaux mouvements. D'abord pour mélanger des couleurs, puis pour dessiner des formes.

Exercices

Regardez cette table d'équations, réalisée par Kynd. Voyez comme il combine les fonctions et leurs propriétés pour contrôler les variations de valuer entre 0 et 1. A présent, c'est à votre tour de vous entraîner à reproduire ces fonctions. Souvenez vous que plus vous pratiquerez, meilleur sera votre karaté.

Kynd - www.flickr.com/photos/kynd/9546075099/ (2013)

Pour la boîte à outils

Voici quelques outils qui simplifient la visualisation des fonctions.

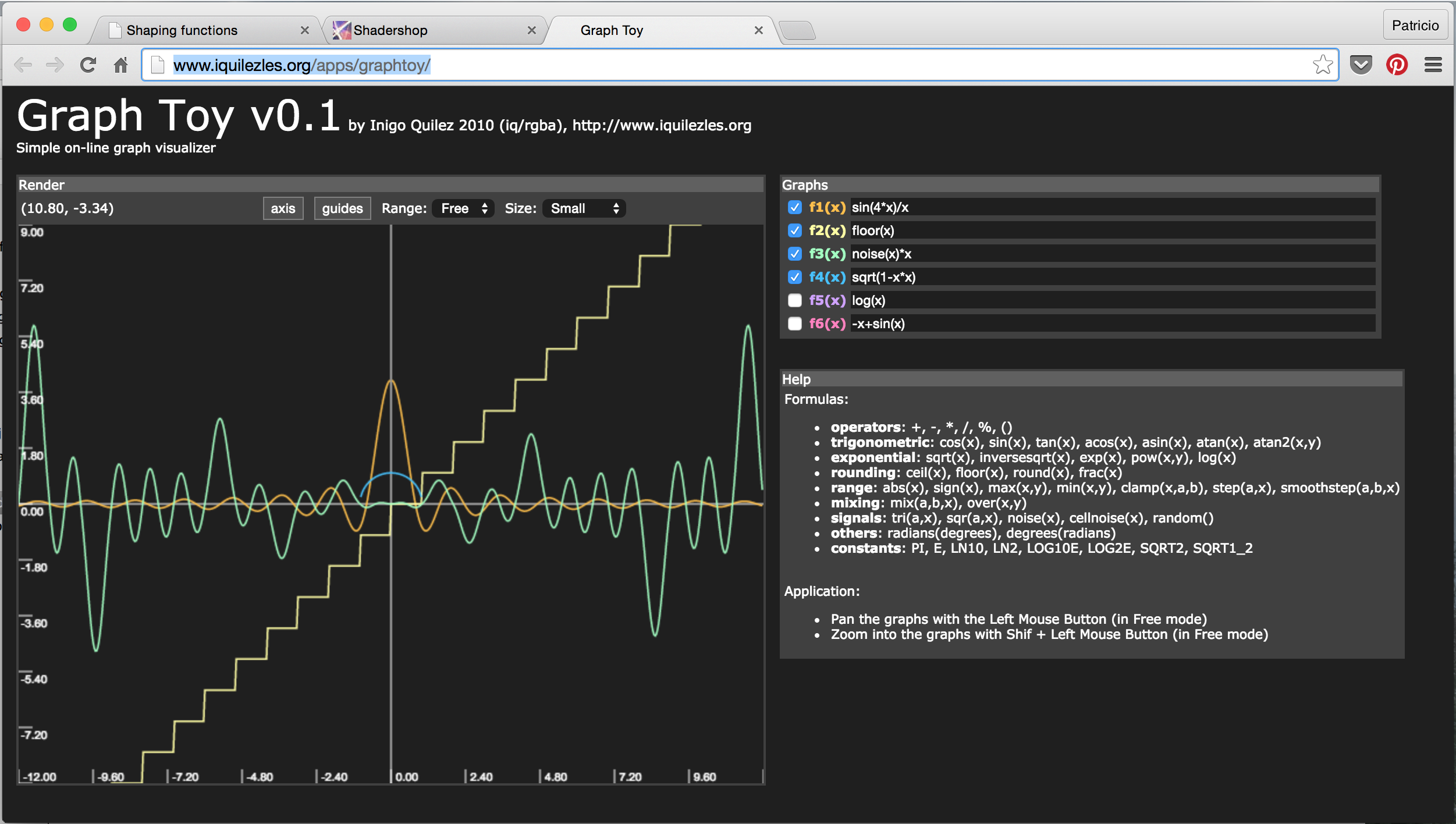
Iñigo Quilez - GraphToy (2010)