Dibujando con algoritmos

Funciones de forma

Este capítulo se podría llamar "La lección de la cerca del Sr Miyagi". Anteriormente normalizamos la posición de x e y al canal de rojo y verde. Esencialmente creamos una función que tomaba dos vectores dimensionales (x e y) y devolvía un vector de cuatro dimensiones (rojo, verde, azul y transparencia). Pero antes de ir más lejos, transformando valores entre dimensiones, necesitamos comenzar con algo sencillo... mucho más sencillo. Eso significa comprender las funciones unidimensionales. A mayor tiempo y energía que pongas en aprender esto, mejor será tu karate.

El siguiente código va a ser nuestra cerca. Dentro del código visualizamos el valor normalizado de la coordenada x (st.x) de dos maneras: una visualizando el brillo (observa el bonito gradiente de fondo del negro al blanco) y otra dibujando una línea verde arriba (en este caso el valor de x es asignado directamente al valor de y). No te enfoques mucho en la función plot, la veremos en detalle en unos momentos.

Nota rápida: el constructor de vec3 "entiende" que quieres asignar tres colores con la misma variable, mientras que el vec4 entiende que quieres crear un vector tridimensional con un cuarto valor (en este caso el que controla el alpha). Mira por ejemplo la línea 19 y la 25 de arriba.

Este código es tu cerca; es importante observarlo y entenderlo. Volverás aquí una y otra vez, a este espacio entre el 0.0 y el 1.0. Aprenderás el arte de doblar y dar forma a esta línea.

Esta relación par entre x e y (o el brillo) es conocida como interpolación lineal. Desde aquí podemos utilizar funciones matemáticas para darle forma a esta línea. Por ejemplo podemos elevar x a la quinta potencia para generar una línea curva.

Interesante ¿No? En la línea 22 puedes probar diferentes exponentes: 20.0, 2.0, 1.0, 0.0, 0.2 o 0.02 por ejemplo. Entender esta relación entre el valor y el exponente nos será muy útil. Usar este tipo de funciones matemáticas aquí y allá nos dará un control expresivo sobre nuestro código, como si fuese un tipo de acupuntura con el que manejas el flujo de los valores.

pow() es una función nativa en GLSL y hay muchas más. La mayoría de ellas son aceleradas por hardware, lo que significa que, usadas de la forma correcta, harán tu código mucho más rápido.

Reemplaza la función de la línea 19. Prueba otras como: exp(), log() y sqrt(). Algunas de estas funciones son mucho más interesantes cuando las usamos con PI. En la línea 8 definí un macro que reemplaza cualquier llamado a PI por el valor 3.14159265359.

Step y Smoothstep

GLSL también cuenta con algunas funciones únicas de interpolación, que también son aceleradas por hardware.

La interpolación step() recibe dos parámetros. El primero es el límite o umbral, el segundo es el valor que queremos chequear. Cualquier número por debajo del límite devuelve 0.0 todo lo que lo supere devuelve 1.0.

Intenta cambiar el límite en la línea 20 del siguiente código.

La otra función única es el smoothstep(). Dado un rango de dos números y un valor, esta función interpola el valor entre el rango definido. Los primeros dos parámetros son para el comienzo y el final de la transición, el tercero es el valor a interpolar.

En el anterior ejemplo, en la línea 12, hemos usado smoothstep para dibujar una línea verde en la función plot(). Por cada posición en el eje x esta función crea una salto en un valor particular de y. ¿Cómo? Conectando dos smoothstep() juntos. Observa la siguiente función y reemplaza la línea 20 por esta, y piensa en ella como un corte vertical. El fondo se parece a una línea ¿No?

    float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);

Seno y Coseno

Cuando queremos usar un poco de matemática para animar, dar forma o mezclar valores, no hay nada mejor que ser amigos del seno y del coseno.

Estas dos funciones básicas trigonométricas trabajan juntas creando círculos y son más útiles que la navaja suiza de MacGyver. Es importante saber como se comportan y de que forma pueden ser combinadas. En pocas palabras, dado un ángulo (en radianes) devolverán la posición de x (coseno) e y (seno) de un punto en el borde de un círculo con un radio igual a 1. Como estas funciones devuelven un valor normalizado (entre -1 y 1) y suavizado, terminan siendo una herramienta increíble.

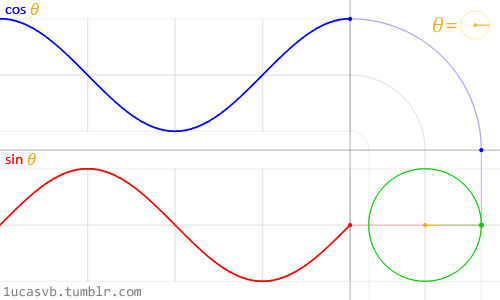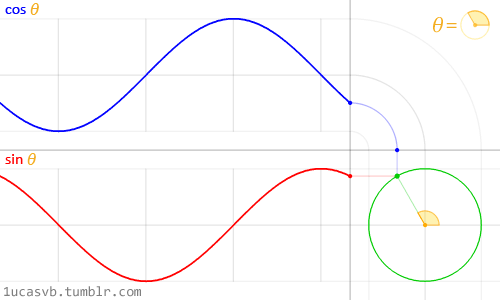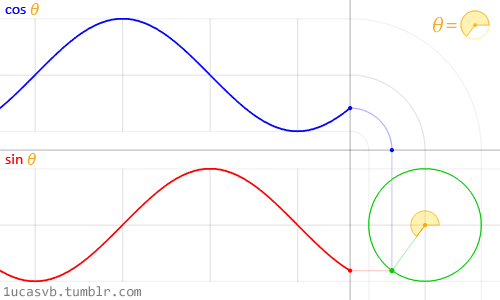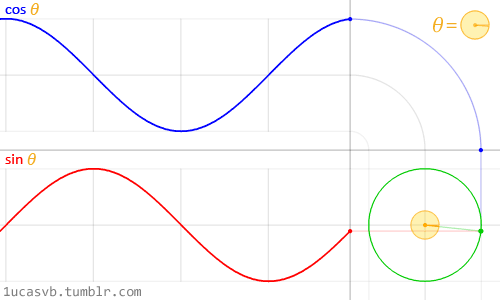
Como es difícil describir la relación entre las funciones trigonométricas y los círculos, la hermosa animación de arriba hace el trabajo de explicarlo visualmente.

Presta mucha atención a esta curva sinusoidal. Nota como los valores de Y fluyen suavemente entre -1 y 1. Como vimos en el anterior capítulo, podemos utilizar el comportamiento rítmico de sin() para animar propiedades. Si estás leyendo este ejemplo en un navegador, puedes modificar la fórmula que aparece aquí arriba y ver cómo cambia la onda. (Nota: No olvidar el punto y coma al final.)

Completa los siguientes ejercicios y presta atención a lo que sucede:

• Suma el tiempo (u_time) a x antes de computar el sin. Observa detenidamente ese movimiento a lo largo de x.

• Multiplica x por PI antes de computar el sin. Nota como las dos fases se encogen y cada ciclo se repite dos veces.

• Multiplica el tiempo (u_time) por x antes de computar el sin. Observa como la frecuencia entre las fases se comprime más y más. Nota que u_time en un momento pasa a ser un número muy alto y se hace difícil ver el gráfico.

• Suma 1.0 a sin(x). Observa como toda la onda es desplazada hacia arriba y ahora todos los valores van de 0.0 a 2.0.

• Multiplica sin(x) por 2.0. Mira como la amplitud duplica su tamaño.

• Calcula el valor absoluto (abs()) de sin(x). Observa como se parece a la trayectoria de una pelota rebotando.

• Extrae sólo la parte fraccionaria (fract()) del resultado de sin(x).

• Suma el mayor entero más cercano (ceil()) y el menor entero más cercano (floor()) del resultado de sin(x) para obtener la onda digital de 1.0 y -1.0.

Otras funciones útiles

Al final del último ejercicio hemos introducido algunas funciones nuevas. Ahora es el momento de experimentar con cada una descomenteando las siguientes lineas, de a una. Es importante entender estas funciones y estudiar como se comportan. Ya lo sé ¿Para qué? Si buscas rápidamente en Google "Arte Generativo" vas a entender el por qué. Ten en cuenta que estas funciones son nuestra cerca. Estamos dominando el movimiento en una sola dimensión, arriba y abajo. ¡Pronto, será el momento de agregar la segunda, la tercera y la cuarta dimensión!

Funciones de forma avanzadas

Golan Levin tiene en su página documentación muy útil sobre cómo generar formas complejas con funciones. Trasladar estas funciones a GLSL es una muy buena forma de comenzar a generar nuestras propias piezas de código.

• Polynomial Shaping Functions: www.flong.com/archive/texts/code/shapers_poly

• Exponential Shaping Functions: www.flong.com/archive/texts/code/shapers_exp

• Circular & Elliptical Shaping Functions: www.flong.com/archive/texts/code/shapers_circ

• Bezier and Other Parametric Shaping Functions: www.flong.com/archive/texts/code/shapers_bez

Como los chefs que colectan especias e ingredientes exóticos, los artistas digitales y creative coders tienen un amor particular por crear sus propias funciones de dibujo.

Iñigo Quiles tiene una gran colección de funciones útiles. Después de leer este artículo echa un vistazo a la traducción de esas funciones a GLSL. Presta atención a los pequeños cambios necesarios, como poner "." (punto) en los valores flotantes y usar los nombres en GLSL de las funciones en C; por ejemplo en vez de powf() usamos pow():

• Impulse
• Cubic Pulse
• Exponential Step
• Parabola
• Power Curve

Para que te mantengas motivado, aqui hay un elegante ejemplo (hecho por Danguafer) de alguien que logró dominar su karate en las funciones.

En el Siguiente >> capítulo comenzaremos a usar nuevos movimientos. Primero mezclaremos color y luego dibujaremos formas.

Ejercicio

Presta atención a la siguiente tabla de ecuaciones hecha por Kynd. Observa como combina las funciones y sus propiedades para controlar los valores de 0.0 a 1.0. Ahora es el momento de practicar replicando estas funciones. Recuerda que cuanto más practiques esto, mejor será tu karate.

Para tu caja de herramientas

Estas son algunas herramientas que te ayudarán a visualizar este tipo de funciones.

• GraphToy: una vez más Iñigo Quilez ha creado una herramienta para visualizar funciones GLSL en WebGL.

• LYGIA Shader Library a shader library of reusable functions that can be include easily on your projects. It's very granular, designed for reusability, performance and flexibility. And can be easily be added to any projects and frameworks.