Rysowanie algorytmiczne

Shaping functions

Rozdział ten mógłby się nazywać "lekcja płota Pana Miyagiego". Poprzednio, mapowaliśmy znormalizowane pozycje x i y do czerwonego i zielonego kanału. W skróćie, stworzyliśmy fumkcję, która przyjmuje dwuwymiarowy wektor (x i y) i zwraca czterowymiarowy wektor (r, g, b i a). Jednak zanim zagłębimy się w takie transformacje między wymiarami, wypada najpierw opanować tworzenie jednowymiarowych funkcji w pełni. Im więcej czasu spędzisz na szlifowaniu tej umiejętności, tym lepsze będzie twoje "shader karate".

Poniższy kod będzie naszym płotem. Wizualizujemy w nim znormalizowaną wartość współrzędnej x (st.x) w dwojaki sposób: poprzez jasność (zauważ płynny gradient od czerni do bieli) oraz przez rysowanie zielonego wykresu funkcji (w poniższym przykładzie funkcji x = y). Nie przejmuj się za bardzo funkcją plot - wrócimy do niej później.

Krótka uwaga: Konstruktor typu vec3 "rozumie", że chcesz przypisać tę samą wartość do każdego z trzech kanałów koloru, natomaist typu vec4 rozumie, że chcesz stworzyć czterowymiarowy wektor z wektora trójwymiarowego i czwartej wartości (w tym wypadku wartość ta kontroluje alphę, czyli przezroczystość). Spójrz na linjki 19 i 25 powyżej.

Kod jest twoim płotem - ważne, żebyś umiał na niego spojrzeć i go zrozumieć. Zakres od 0.0 do 1.0 będzie ci stale towarzyszył. Opanujesz sztukę blendowania (pol. "mieszania", "łączenia") i kształtowania tej linii

Tę wzajmnie jednoznaczną (ang. "one-to-one") funkcję między x i y (lub jasnością) nazywamy interpolacją liniową. Możemy użyć funkcji matematycznych by uformować tę linię. Przykładowo, możemy podnieść x do potęgi 5, aby utworzyć krzywą linię.

Ciekawe, prawda? W linijce 22 spróbuj użyć następujących wykładników: 20.0, 2.0, 1.0, 0.0, 0.2 lub 0.02. Zrozumienie związków między końcową wartością a wykładnikiem będzie bardzo przydatne. Używanie tego typu funkcji matematycznych tu i tam da ci pełnię kontroli nad twoim kodem.

pow() to natywna funkcja w GLSL, więc zaimplementowana jest na poziomie hardware'u, co oznacza większą wydajność.

Zastąp funkcję potęgową w linijce 22 inną natywną funkcją. Spróbuj exp(), log() i sqrt(). W wypadku funkcji trygonometrycznych warto użyć liczby PI. Jest ona zdefiniowana w 8 linijce za pomocą makra, który zastąpi każde użycie PI wartością 3.14159265359.

Step i Smoothstep

GLSL posiada też unikalne natywne funckje interpolacyjne wykorzystujące akcelerację sprzętową.

Funkcja step() otrzymuje dwa argumenty. Pierwszy z nich to limit lub próg, natomiast drugi to wartość, którą chcemy porównać z tym progiem. Każda wartość poniżej limitu zwróci 0.0, natomiast wszystko powyżej limitu zwróci 1.0.

Spróbuj zmienić tę wartość progową w linijce 20 poniższego kodu.

Druga unikalna funkcja znana jest jako smoothstep() i otrzymuje trzy argumenty Dwa pierwsze argumenty służą do określenia początku i końca interpolacji (tranzycji/przejścia), natomiast trzeci jest wartością interpolowaną.

W poprzednim przykładzie, w linii 12, zauważ, że użyliśmy smoothstep wewnątrz funkcji plot() do narysowania zielonej linii. Dla każdej pozycji wzdłuż osi x funkcja ta zwraca odpowiednią wartość y. Jak? Poprzez połączenie ze sobą dwóch smoothstep(). Spójrz na poniżśzy fragment kodu (zauważ, że jest analogiczny do kodu w funkcji plot()) i wstaw go w linijce 20 powyższego przykładu. Wyobraź sobie, że widoczny wykres o kształcie dzwona (o kształcie rozkładu normalnego) "wędruje" wzdłuż funkcji przekazanej do argumentu pct funkcji plot().

float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);

Sinus i Cosinus

Kiedy chcesz użyć matematyki do animacji, kształtowania lub blendowania wartości, nie ma nic lepszego niż zaprzyjaźnienie się z sinusem i cosinusem.

Te dwie podstawowe funkcje trygonometryczne współpracują ze sobą, aby skonstruować okręgi, które są tak poręczne jak szwajcarski scyzoryk MacGyvera. Warto wiedzieć, jak się zachowują i na jakie sposoby można je łączyć. W skrócie, otrzymawszy kąt (w radianach), zwrócą one współrzędne x (cosinus) i y (sinus) punktu na brzegu okręgu o promieniu równym 1. Jednak fakt, że zwracają one znormalizowane wartości (wartości pomiędzy -1 a 1) w tak płynny sposób, czyni z nich niesamowite narzędzie.

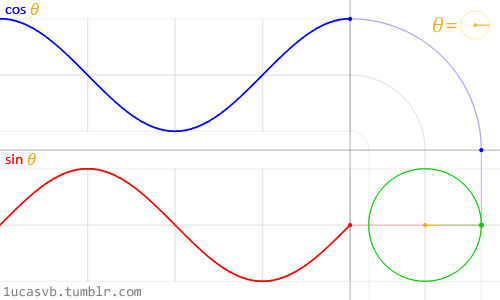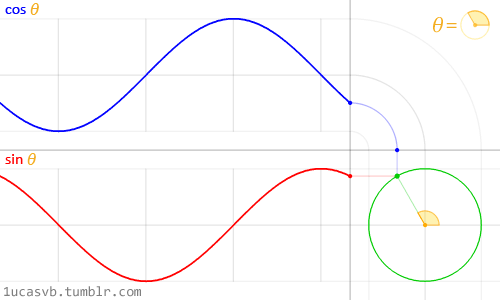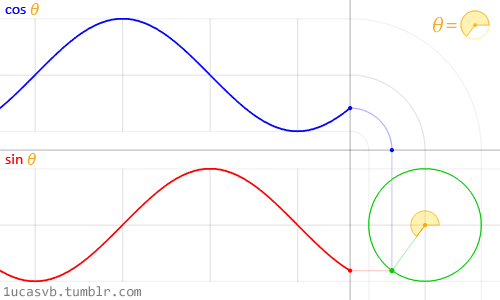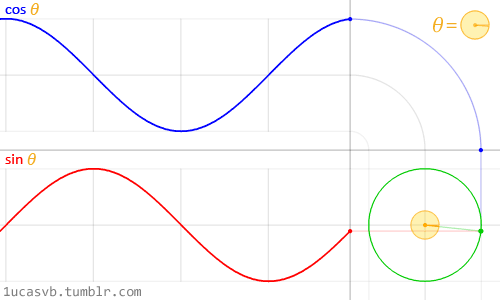
Choć trudno opisać wszystkie związki między funkcjami trygonometrycznymi i okręgami, powyższa animacja pięknie je wizualizuje.

Przyjrzyj się uważnie powyższej fali sinusoidalnej. Zauważ, jak wartości y oscylują płynnie między +1 a -1. Jak widzieliśmy w przykładzie z czasem w poprzednim rozdziale, możesz wykorzystać to rytmiczne zachowanie sin() do animowania dowolnych wartości. Jeśli czytasz ten przykład w przeglądarce, spróbuj zmienić kod w powyższym jedno-linjkowym przykładzie i zaobserwuj, jak zmienia się fala. (Uwaga: nie zapomnij o średniku na końcu linii).

Spróbuj następnujących ćwiczeń i zobacz, co się stanie

• Dodaj czas (u_time) do x wewnątrz funkcji sin. Zapamiętaj ten ruch wzdłuż x.

• Pomnóż x przez PI wewnątrz funkcji sin. Zauważ, jak okres sinusa zmniejsza się do 2. Zwiększyliśmy w ten sposób częstotliwość.

• Pomnóż czas (u_time) przez x wewnątrz funkcji sin. Zobacz jak częstotliwość zwiększa się, a okres maleje. Możliwe że u_time może być już bardzo duży, co czyni wykres trudnym do odczytania - odśwież stronę i spróbuj ponownie.

• Dodaj 1.0 do sin(x). Zobacz jak cała fala jest przesunięta w górę i wszystkie wartości są pomiędzy 0.0 a 2.0.

• Pomnóż sin(x) przez 2.0. Zobacz jak amplituda podwaja się.

• Oblicz wartość bezwzględną (abs()) funkcji sin(x). Wygląda to jak ślad odbijającej się piłki.

• Wyciągnij tylko część ułamkową (fract()) z funkcji sin(x).

• Dodaj sufit (ceil()) oraz podłogę (floor()) z sin(x), aby otrzymać falę cyfrową o wartościach 1 i -1.

Kilka dodatkowych przydatnych funkcji

Pod koniec ostatniego ćwiczenia wprowadziliśmy kilka nowych funkcji. Teraz czas na eksperymentowanie z każdą z nich poprzez odkomentowanie poniższych linii po kolei. Poznaj te funkcje i zbadaj jak się zachowują. Wiem, zastanawiasz się... dlaczego? Szybkie wyszukiwanie w google "generative art" powie Ci to. Pamiętaj, że te funkcje to nasz płot. Opanowujemy ruch w jednym wymiarze, w górę i w dół. Już niedługo przyjdzie czas na dwa, trzy i cztery wymiary!

Zaawansowane funkcje kształtujące

Golan Levin ma świetną dokumentację bardziej złożonych shaping functions, które są niezwykle pomocne. Samodzielene przeniesienie ich do GLSL jest dobrym krokiem w stronę budowania własnego zasobu snippetów kodu.

• Wielomianowe shaping fucntions: www.flong.com/archive/texts/code/shapers_poly

• Wykładnicze shaping functions: www.flong.com/archive/texts/code/shapers_exp

• Kołowe i Eliptyczne shaping functions: www.flong.com/archive/texts/code/shapers_circ

• Parametryczne (Beziera) shaping functions: www.flong.com/archive/texts/code/shapers_bez

Podobnie jak szefowie kuchni, którzy zbierają przyprawy i egzotyczne składniki, artyści cyfrowi mają szczególne zamiłowanie do pracy nad własnymi shaping functions.

Iñigo Quiles ma wspaniałą kolekcję użytecznych funkcji. Po przeczytaniu tego artykułu spójrz na poniższe tłumaczenie tych funkcji na GLSL. Zwróć uwagę na małe zmiany, jak stawianie "." (kropki) przy liczbach zmiennoprzecinkowych i używanie nazw GLSL dla funkcji z C (na przykład zamiast powf() użyj pow()):

Aby podtrzymać twoją motywację, oto elegancki przykład (wykonany przez Danguafer) ilustrujący opanowanie karate shaping functions.

W następnym rozdziale zaczniemy używać naszych nowych sztuczek. Najpierw z mieszaniem kolorów, a potem z rysowaniem kształtów.

Ćwiczenia

Przyjrzyj się poniższej tabeli wzorów wykonanej przez Kynd. Zobacz jak łączy on funkcje i ich właściwości, aby kontrolować wartości pomiędzy 0.0 a 1.0. Teraz nadszedł czas, abyś poćwiczył, odtwarzając te funkcje. Pamiętaj im więcej będziesz ćwiczył tym lepsze będzie twoje karate.

Pomocne narzędzia

Oto kilka narzędzi, które ułatwią ci wizualizację tego typu funkcji.

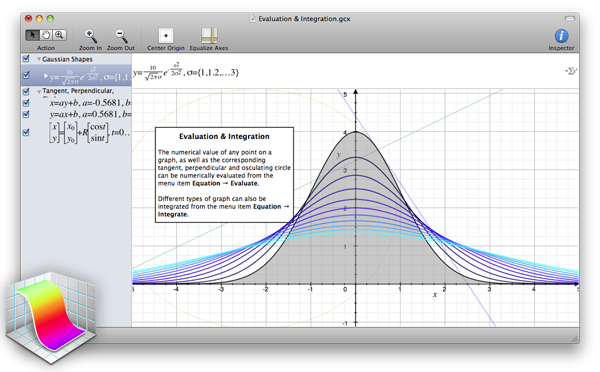
• Grapher: jeśli masz komputer z systemem MacOS, wpisz grapher w swoim Spotlight, a będziesz mógł użyć tego super poręcznego narzędzia.

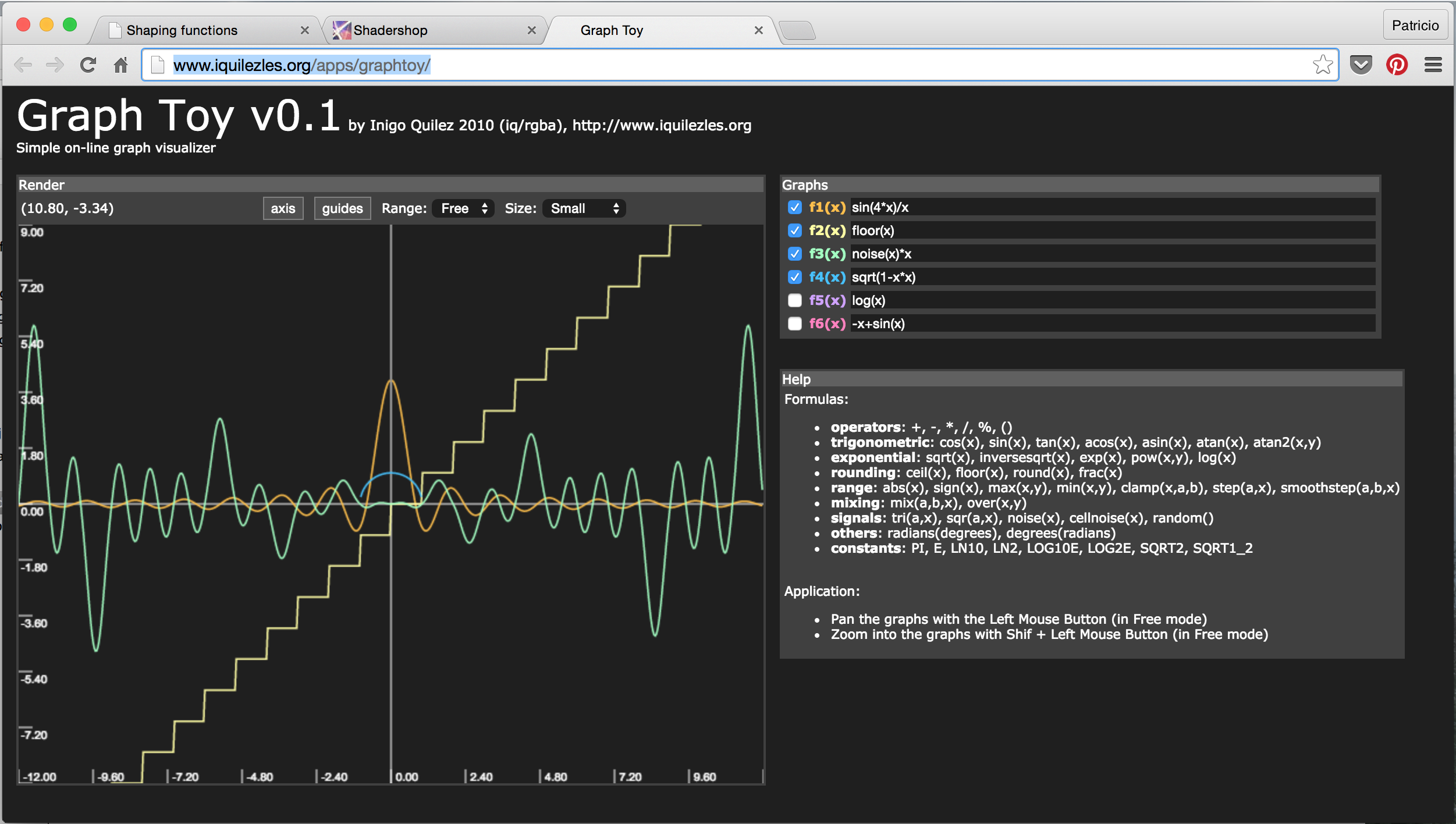
• GraphToy: po raz kolejny Iñigo Quilez stworzył narzędzie do wizualizacji funkcji GLSL w WebGL.

• Shadershop: to niesamowite narzędzie stworzone przez Toby Schachman nauczy cię jak konstruować złożone funkcje w niesamowicie wizualny i intuicyjny sposób.